基于MERS的永磁风力发电机电抗补偿策略*
李 杰, 屈克庆
(1.上海开放大学信息与工程系,上海 200433;
2.上海电力学院电力与自动化工程学院,上海 200090)
0 引言
在直驱式风力并网发电系统中采用双PWM变流器可以改善机侧谐波,提高系统的输出能力,但是成本较高,控制也较复杂,另外发电机和机侧变流器之间还必须有滤波装置,也增加了系统的损耗。如果变流系统机侧采用无源整流,则结构简单,控制方便,但发电机交流电抗对于直驱式风电系统的输出能力影响显著。采用无源整流时,由于两个原因导致发电机输出功率减小:(1)电流波形不是正弦波,低次谐波造成发电机的损耗增加;(2)整流器交流进线电抗造成的换向重叠角,使电流基波相位滞后,整流电压降低,输出功率减小[1]。
文献[2]指出,在通常的整流装置中,交流进线电抗是整流变压器的漏抗,值很小,对输出功率的影响小。但是在直驱式永磁同步风电系统无源整流结构中,进线电抗是永磁发电机的同步电抗,其值很大,对输出功率的影响亦很大。要想无源整流和有源整流输出同样功率,必须加大发电机,使电机造价约增加40%,反而抵消了无源整流器简单、便宜带来的好处。
因此,对于直驱式永磁同步机风电系统而言,要想使得系统既结构简单又真正意义上缩减成本,尽量消除永磁同步发电机交流电抗的影响是必要的工作。近年来一种被称为磁能恢复开关(Magnetic Energy Recovery Switch,MERS)的拓扑受到了研究人员的重视,并进行了一些研究[3-7]。MERS可用于任何需电抗补偿的场合,因此也可以用于永磁同步机风力发电场合。本文详细分析了MERS的工作原理,并研究了其在永磁同步机风电系统中的应用及控制方法,给出仿真结果。
1 MERS系统结构及工作原理
MERS的基本结构如图1中大虚框内所示。4个IGBT(或MOSFET)构成两条并联桥臂,每个桥臂上串联两个IGBT。每个IGBT都反并联一个二极管,并且每个IGBT都与所串联的IGBT及所并联IGBT反向。桥臂中点连有一个电解电容。MERS被串联在交流电源和负载之间,它能够吸收储存在电路电感中的磁能,也能把磁能恢复到负载上。通过改变MERS的开关相位角还可以控制电流的相位。S1、S3的开关相位设置为超前电源电动势90°时,电感上的感性电压就可以被电容的电压补偿掉,这样的话,还能使电路的功率因数为1。

图1 MERS基本结构及应用
为了分析方便,首先假设电流连续,且忽略电源内阻,则在没有MERS的情况下,基波矢量关系如图2(a)所示,其中E为电动势,I为电流,UL为电感两端电压,Uo为电阻负载两端电压,可以看出在电感的作用下,Uo小于E;而在图2(b)中应用MERS的情况下,利用UMERS抵消了UL的作用,则Uo等于E,提高了功率因数,进而有效提高了输出电压及系统的效率。
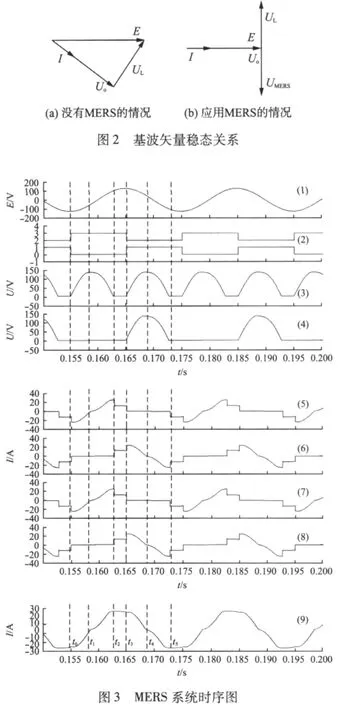
为了详细说明MERS的工作原理,本节给出了仿真时的MERS工作时序图(见图3)和MERS换流过程图(见图4)。在图3中:(1)为电源电动势;(2)为开关信号,其中上面的信号为1、3号开关的开关信号,下面的信号为2、4号开关的开关信号,两者互补,各开通半个周期;(3)为MERS内电容电压;(4)为1号开关两端承受的电压;(5)~(8)分别为1~4号开关的电流波形;(9)为负载上电流波形;(2)中的开关信号如上所述领先电源电动势90°。下面从t0开始分析。
t0时刻,电动势刚好为负的最大值;按照上述触发规则,此时 S1、S3触发,S2、S4关闭;由图3可知,此时MERS内电容电压UM为零,负载电流为负。在t0时刻之后,虽然S1、S3上已经有触发信号,不过由于其各自反并联的二极管VD1、VD3均导通,S1、S3承受反压而没有开通,此时负的电流经VD1、VD3续流,且开始给电容CM充电,电感中的能量逐渐释放到电容中,如图4(a)所示。
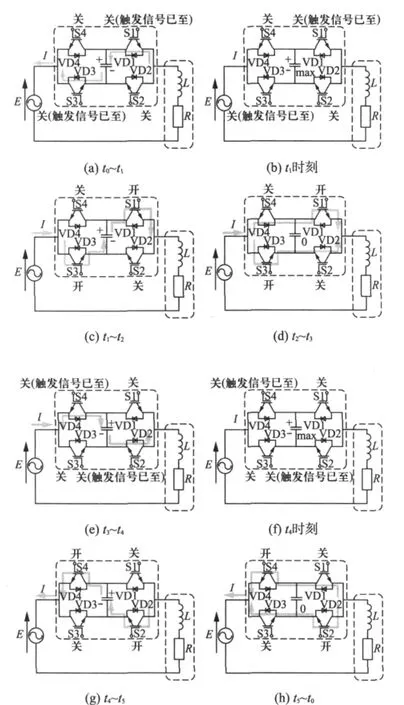
图4 MERS换流过程
随着MERS电容电压UM的不断增加,负的电流逐渐减小,在t1时刻,UM到达最大值,而此时电流为零,如图4(b)所示。
t1时刻之后,在E、UM、UL的共同作用下,MERS电容开始通过 S1、S3放电,电流为正,而VD2、VD4由于承受反压而没有导通,在t0~t1时段电感存储于CM的能量重新释放出来,电路工作情况如图4(c)所示。
t2时刻,MERS电容电压下降到零,之后VD2、VD4导通,由于两路器件参数完全相同,所以电流均分为两路分别经VD4-S1和S3-VD2流过,如图4(d)所示。由图3中(5)~(8)亦可看出此时电流经由上下两路均分。
t3时刻,S2、S4 触发,S1、S3 关闭,此时由于电感的存在,电流通过VD2、VD4续流,并重新开始给电容充电,而S2、S4由于VD2、VD4导通,从而承受反压无法导通,t3~t4时刻电路工况如图4(e)所示。
与t1时刻相同,随着UM的不断增加,正的电流逐渐减小,在t4时刻UC到达最大值,此时电流为零,如图4(f)所示。
t4之后,在E、UM、UL的共同作用下,电流负向增加,电容放电,电流流经S2、S4,电路工作情况如图4(g)所示。
在t5时刻,电容电压下降为零,负的电流分别经VD1-S4及S2-VD3流过,由于器件参数相同,所以两路均流,电路工作情况如图4(h)所示。这个均流过程结束后,电路又回到t0时刻的工况。
2 基于MERS的永磁同步机风电系统及其补偿控制
前文指出,使用二极管整流桥的直驱式风电系统由于发电机同步电抗的原因,随着电流的上升整流桥输出电压会减小。如果能将上述MERS装置应用于这种风电系统,则有望提高系统的输出能力。MERS能改善机侧功率因数,还能产生电压来补偿发电机同步电抗的影响。电机输出电压越高,越能提高风力发电系统的输出功率和效率。
图5是带有MERS的永磁同步机风力发电系统结构框图。当MERS应用于永磁同步风电系统时,由于系统为三相系统,所以应该如图5所示,在发电机每一相输出串接一个MERS网络。为了便于分析,假设电流连续且负载为纯阻型,并只对一相进行分析。图6是同步发电机和MERS串联的等效电路。同步机的等效电路由感应电动势和同步电抗xs以及电枢绕组电阻rs的串联来表示。在一个不带MERS的系统中,假设负载的功率因数为1,输出端电压0由式(1)表示:


图7是带MERS的永磁同步发电机的向量图。感应电动势与输出电流同相位。由于MERS的功率因数控制和电抗电压补偿作用,输出电压的压降只是绕组电阻压降,与没有MERS系统相比,有MERS系统的输出电压提高。
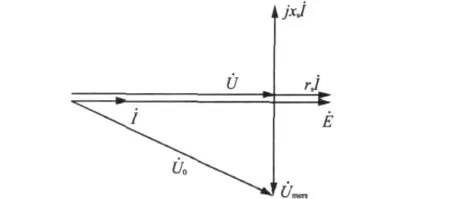
图7 永磁同步发电机和MERS串联的向量图
MERS控制简单,没有闭环控制系统。在永磁同步机风力发电系统中,只需要通过测速光电码盘确定感应电动势的初始相位(感生电动势矢量超前永磁体磁链矢量90°),就可以按上述控制思路来驱动MERS装置上IGBT的开通与关断,从而实现发电机电抗的补偿和功率因数的校正。这样的系统需要12个IGBT器件,同其他有源补偿电路相比,其开关导通损耗较大。但是由于系统中MERS的开关频率和电枢电压频率相同,IGBT的开关损耗很小甚至可以忽略,此外还省去了滤波电感的损耗,因此总体上损耗反而减少[4]。
3 仿真研究
本文对带MERS的永磁同步发电机电抗补偿策略进行了仿真研究。由于MERS装置设计的关键是其中电容与待补偿系统的匹配问题,因此有必要先研究电容CM的选取原则。为此按图6进行了单相电路的仿真研究,电路输出端接一个负载电阻。仿真参数如下:电源电动势幅值130 V,频率50 Hz,电源内阻 1.55 Ω,电源内部电感8.12 mH,直流侧电容1 200 μF。每次改变CM的值,并相应改变负载电阻的大小,使每次仿真电源输出功率大致一致,以期比较在输出功率相同的情况下,CM对MERS补偿效果的影响。
仿真结果如图8及表1所示。图8中(1)为电网电动势;(2)为交流侧电流;(3)为MERS网络中CM电压UM;(4)为直流整流电压。

表1 MERS网络中CM取不同值时的对比
通过图8及表1中的对比可看出,当CM超过某一临界值之后,随着CM的增加MERS的补偿效果除了在THD降低方面略有加强,其他效果就基本保持不变,而当CM在这个临界值以下时,随着CM的增加,MERS的补偿效果亦随之增强。通过仿真研究发现,此临界值即电路中的电容谐振值,以图8及表1的仿真为例,电源频率为50 Hz,电源内部电感为8.12 mH,则谐振电容值为

由于此时网侧电流并不是完全的正弦波,实际的临界电容值会比上述CR略小,故设计MERS系统时,CM取值为CR即可。但是对于永磁同步风电系统而言,发电机电动势随着转速的不同而不同,为了能在所有工况下MERS都能完全发挥功效,应以按照系统最大转速所对应的发电机电动势频率来计算CM值。需指出的是当CM超出临界电容值之后,CM不会放电至零,所以不存在换流分析过程中两路均流的过程,即图4(d)、4(h)中的电路工作情况。

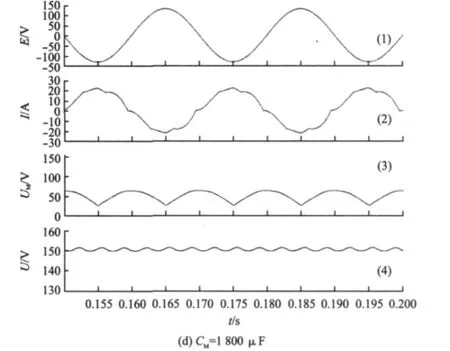
图8 输出功率相同时CM不同取值的对比
对于MERS装置在永磁同步机风力发电系统中对发电机电抗补偿的作用,本文也进行了仿真研究。仿真参数如下:永磁同步发电机内阻1.7 Ω,同步电抗 3 mH,每极磁通量0.371 4 Wb,转动惯量 10 kg·m2,36对极,摩擦系数 1×10-3N·m·s。MERS 电容CM为150 μF;直流侧电容Cdc为1 200 μF。在永磁同步风电系统中,当系统处于稳定工作状态时,整流桥直流侧功率输出稳定,可以用一个电阻R来代替表示。仿真过程中,通过调整直流侧电阻R的值使得每次发电机相电流有效值相同,以此来比较相同条件下应用了MERS的系统与未应用MERS的系统的性能差异;另外发电机采用恒转速输入,这样发电机电动势的幅值与频率亦保持恒定,由于转速为30 rad/s,所以有如图9所示为负载较大、发电机输出电流连续的情况下,应用MERS与不用MERS的情况比较,其中(1)为发电机反电动势;(2)为发电机输出电流;(3)为直流输出电压。具体数值记录在表2中。从表2可看出,在发电机输出相电流相同的情况下,通过MERS的补偿作用,功率因数被校正为接近1,输出电压大幅提高,输出有功功率也大大增加,只是谐波略有增加,但相比其优点而言可以忽略,上述效果亦可从图9中直接看出。


表2 电流连续时MERS的补偿效果

图9 电流连续时MERS的补偿效果
以上分析中一直假设电流连续,此处做了电流不连续情况下的仿真,如图10所示,具体数据记录在表3中。与电流连续情况下类似,应用MERS后功率因数被校正为1,输出电压提高,输出有功功率也增加,而且这时电流谐波反而下降。

表3 电流不连续时MERS的补偿效果
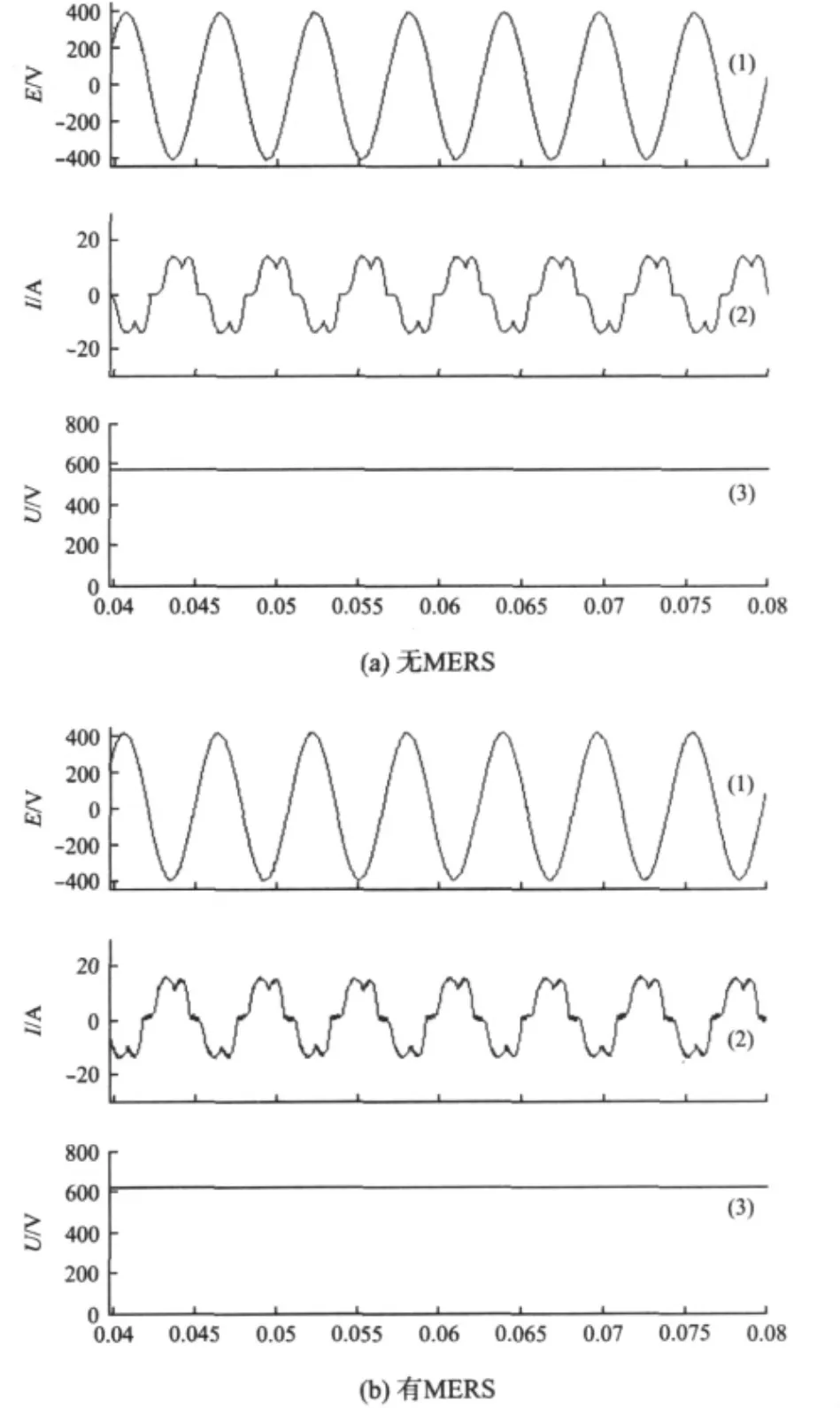
图10 电流不连续时MERS的补偿效果
图11(a)是有MERS系统和无MERS系统在发电机相电流与直流侧输出功率关系曲线中的对比,显然相同相电流下,有MERS系统比无MERS系统的输出能力强。图11(b)是有MERS系统和无MERS系统在发电机相电流与直流侧输出电压关系曲线中的对比,显然在相同相电流下,有MERS系统比无MERS系统的直流输出电压高,重载下的输出特性更硬一些。

图11 直流侧输出功率和电压对发电机相电流的关系图
4 结语
通过上文的理论分析和仿真可知,MERS能改善永磁同步机风力发电系统机侧功率因数,并产生电压来补偿发电机同步电抗的影响,从而提高了风电系统的输出功率和效率。尽管这样的系统增加了12个IGBT器件,同其他有源补偿电路相比其开关导通损耗较大,但是由于系统中MERS的开关频率很低,总的开关损耗很小甚至可以忽略,另外省去了滤波电感的损耗,因此总体来看损耗是减少的。总之,MERS装置在提高永磁发电机输出电压和过载能力方面效果显著,且永磁同步发电机表现出和直流发电机一样较硬的输出特性。使用MERS的变流系统有望使带同步电机的风力发电系统结构更加紧凑,同时与传统系统相比在提高系统效率方面大有潜力。
[1]TECK M H N,KELVIN T,SYED I.Mitigation of harmonics in wind turbine driven variable speed permanent magnet synchronous generators[C]∥The 7th InternationalPowerEngineering Conference,2005(2):1159-1164.
[2]马小亮.变速风力发电机组动力驱动系统方案比较[J].变频器世界,2007(4):42-48.
[3]TAKU T,TAKANORI I,JUN N,et al.Power supply for pulsed magnets with magnetic energy recovery current switch[J].IEEE Transactions on Applied Superconductivity,2004,14(2):1794-1797.
[4]TAKU T,GEN H,TAKANORI I,et al.Improved wind power conversion system using magnetic energy recovery switch(MERS)[C]∥Fourtieth IAS Annual Meeting-Industry Applications Conference,2005(3):2007-2012.
[5]TAKANORI I,TAKU T, TAKESHI M, et al.Voltage rating reduction of magnet power supplies using a magnetic energy recovery switch[J].IEEE Transactions on Applied Superconductivity,2006,16(2):1646-1649.
[6]TAKU T,GEN H,TAKANORI I,et al.Application of magnetic energy recovery switch(MERS)to improve output power of wind turbine generators[J].IEEJ Trans IA 2006,126(5):599-604.
[7]郜登科,杨喜军,雷淮刚,等.基于磁能恢复开关的单相串联补偿器的研究[J].华东电力,2008,36(3):47-49.

