等差数列项数N的计算
☉吴东武
等差数列项数N的计算
☉吴东武
吴东武 男,广东省五华县人.1966年毕业于华南工学院化工系无机物工学专业.广州石油化工总厂退休高级工程师,曾从事化工工艺及化工设备技术工作.
前言
等差数列n项和公式Sn,是德国数学家C.F.高斯少年时发现的,此公式人们已经学习了200多年.直至今日,全世界中学数学只教C.F.高斯的等差数列n项和Sn,学生只会计算整数的项数n,而不会计算带小数的项数N.我们的化工专家学者面对等差数列前N项和SN,同样也不会计算带小数的项数N,只好按自己的思维习惯,建立接近实际的计算公式,以解决设计、计算之需.
在上世纪30年代,传热工程出现了一种高效换热设备——螺旋板换热器(如右图),它是由两张厚度为δ的平行钢板卷成,有两条宽度(板间距)为b1和b2的螺旋通道,分别与中央直径为d11与d21的空心半圆柱相通,d11=d21+b1-b2,冷热介质在各自的通道中流动换热,广泛应用于化学工业、制药和食品等领域.螺旋板由里往外各圈长度组成一个等差数列,在螺线长度即等差数列n项和Sn计算中,螺旋圈数即数列的项数
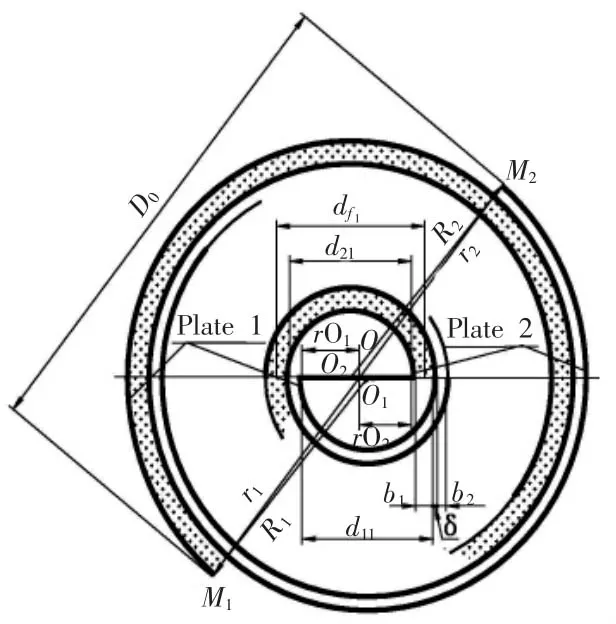
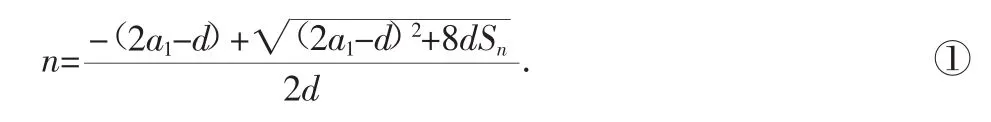
式中的n必须是整数.但是,在设备设计和实际计算中,往往需要用螺旋通道的长度L准确计算带小数的螺旋通道圈数N,准确计算公式是怎样的?
等差数列N项和
在公式导出前,我们先来看看螺旋板长的等差数列是怎样形成的.
螺旋板换热器的卷板过程:当两根不同直径(d11和d21)的半圆柱状的卷辊牢固夹住隔板时,启动卷床,卷辊转动,卷板过程开始.对螺旋板长度而言,长度是从零开始由小至大的过程,是一个程积分过程,也是等差数列的形成过程.首圈长度从0开始,慢慢增长至第一圈长度a1,又从0开始再慢慢增长至第二圈长度a2,…,如此增长至an,此时,由各圈长度构成的等差数列为
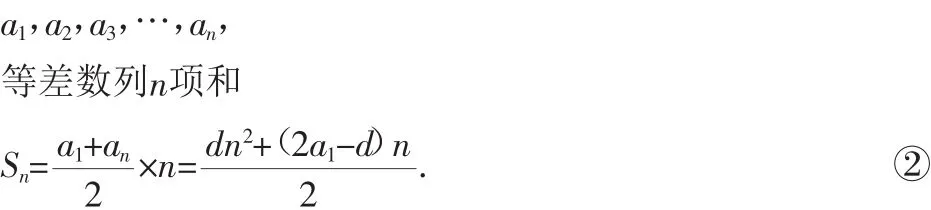
式中a1为等差数列首项,an为整数项,d为公差.
当螺旋板长度增至an后,又继续从0慢慢增长至aN而未到a(n+1),卷床停止.此时,螺旋板圈数由第一圈,第二圈,…,第n圈直至第N圈而未到第(n+1)圈,各圈长度构成的等差数列为
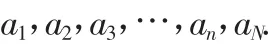
等差数列N项和
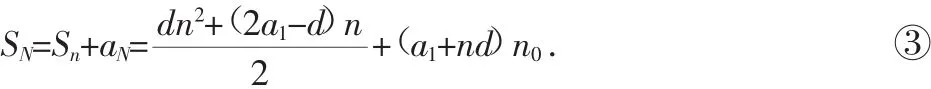
式中n为正整数,0≤n0<1,aN为带小数项.aN在螺旋板换热器中的几何意义是不足一圈的螺线长度.
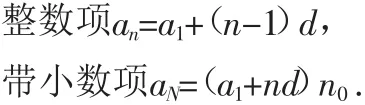
当n0≠0时,等差数列项数N通过下述方法计算:
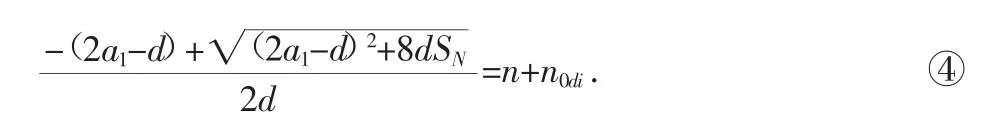
式中n是整数,0≤n0di<1.以式④中的整数n代入③式,计得n0,项数N=n+n0.
我们依据等差数列N项和公式③,可以找出螺旋板换热器螺旋通道长度计算公式:

式中n是整数,0≤n0di<1.以式⑥中的整数n代入⑤式,计得n0,项数N=n+n0.
公式⑤在特定条件n0=0,b=b1=b2,t=2(b+δ),d=d21下,变为

也有文献[1]采用公式⑦计算螺旋通道圈数N.
当n0=0时,N=n,公式⑤的螺旋通道圈数
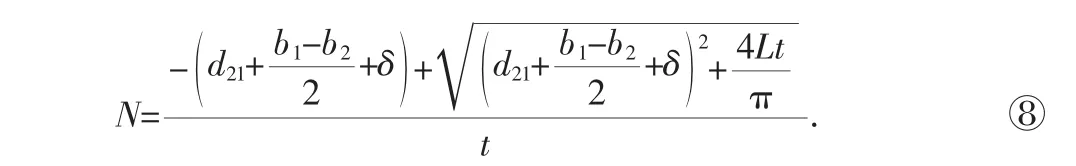
以前,多数文献[2][3][4][5]采用下列公式计算螺旋通道圈数N,其首先使用者是日本学者[6].

同样是不可取.
计算实例(选自参考文献)
设计一台将3000kg/h的煤油从140℃冷却至40℃螺旋板换热器,冷却水入口温度为30℃,冷却水量为15m3/h.
由传热计算得到传热面积A=7.15m2,其中,螺旋板宽H=0.3m,螺旋板2初始内径d21=0.110m,板厚δ=0.0023m,螺旋通道宽b1=0.0093m,b2=0.0042m.
计算螺旋通道圈数N.
解:因为二螺旋通道初始直径df1相等,二通道长度L相等.螺旋通道长度

结论:通过对等差数列的形成过程分析和实例计算可以看出,等差数列n项和Sn是神圣的自然规律,不能更改.Sn是基础,公式③④是由SN计算等差数列项数N的完整而准确的方法,公式⑤⑥是螺旋板换热器由螺旋通道长度L计算螺旋通道圈数N实用、准确的方法,不论N是整数还是带小数.
1.王松汉.石油化工设计手册.北京:化学工业出版社,2002.
2.尾花英朗(日).热交换器设计手册.徐中权.北京∶石油工业出版社,1982.
3.毛希澜.换热器设计.上海:上海科学技术出版社,1988.
4.时钧,汪家鼎,余国琮,等.化学工程手册.北京:化学工业出版社,1996.
5.余国琮.化工机械工程手册.北京:化学工业出版社,2003.
6.化学装置编辑部.螺旋板式热交换器的设计[J].化学装置(日本),1966,8(7):43-49.
7.钱颂文.换热器设计手册.北京:化学工业出版社,2002.
8.董其伍,张垚,等.换热器.北京:化学工业出版社,2009.

