构造函数证明函数背景下的不等式的策略

☉云南省玉溪第一中学 武增明

构造函数证明函数背景下的不等式的策略

☉云南省玉溪第一中学 武增明

纵观近几年高考数学试题，可以看出，在函数背景下考查不等式的证明成为一种新的命题趋势.我们知道，证明函数背景下的不等式的通法，是构造函数法.要解决好此类问题，关键是要构造好相应的函数.从哪里入手，怎么构造，如何构造出适当的、合理的、可行的、易操作的函数，许多同学找不到突破口，甚至感到无所适从.下面就此问题作一些探讨，同时希望能帮助同仁把握这类试题的特点及规律，进行有针对性的复习，供参考.

一、转化为f（a）+g（a）≥f（b）+g（b）型

寻找待证不等式的等价不等式，把等价不等式转化为f（a）+g（a）≥f（b）+g（b）型，观察此等价不等式左右两边的结构，构造函数h（x）=f（x）+g（x）.

例1 （2010年高考辽宁卷·文21）已知函数

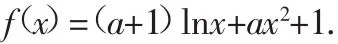
（Ⅰ）讨论函数f（x）的单调性；

（Ⅱ）设a≤－2，

证明：对任意x1，x2∈（0，+∞），|f（x1）－f（x2）|≥4|x1－x2|.

分析：（Ⅰ）略；（Ⅱ）不妨设x1＞x2＞0，由（Ⅰ）知，当a≤－2时，f（x）在（0，+∞）上是减函数，所以f（x1）＜f（x2），即f（x1）－f（x2）＜0，于是|f（x1）－f（x2）|≥4|x1－x2|⇔f（x2）－f（x1）≥4x1－4x2⇔f（x2）+4x2≥f（x1）+4x1.观察此不等式左右两边的结构特征，就会想到构造函数g（x）=f（x）+4x，接下来的工作只需证明函数g（x）=f（x）+4x在（0，+∞）上是减函数就可以了，这时只需要证明g′（x）≤0.

限于篇幅，具体证明过程在这里不再赘述.

点评：找到待证不等式的等价不等式f（x2）+4x2≥f（x1）+4x1，观察此等价不等式左右两边的结构特征，就想到构造函数g（x）=f（x）+4x，然后利用导数就可以轻松获解.这是破解此类问题行之有效的思维途径之一.

（Ⅰ）讨论函数f（x）的单调性；

解答略，留给感兴趣的读者朋友去解答.

二、转化为f（x）≥0（≤0）型

寻找待证不等式的等价不等式，使等价不等式的一端为0，形如f（x）≥0（≤0），由此构造函数g（x）=f（x）.

例3 （2011年高考辽宁卷·理21）已知函数

点评：（1）此种方法，直接移项作差构造函数，利用导数研究函数的单调性或极值进行证明，是常用的一般方法.（2）在这里，若出现g（0）≠0，而是g（0）=m＞0，也可以.同理，若要证明g（x）＜0，而g（0）≠0或g（n）≠0，而是得到g（n）=M＜0，亦即得到g（x）＜g（n）=M＜0，也得到圆满获证.

例4已知函数f（x）=ex－2x+2a.

（Ⅰ）求f（x）的单调区间与极值；

（Ⅱ）求证：当a＞ln2－1，且x＞0时，ex＞x2－2ax+1.

解答略，留给感兴趣的读者朋友去解答.

三、转化为f（x）≥g（x）型

寻找待证不等式的等价不等式，把等价不等式转化为f（x）≥g（x）型，由此构造两个函数h（x）=f（x），u（x）=g（x）.接下来的工作是利用导数判断函数h（x），u（x）的单调性，进而求出函数h（x），u（x）的最值或临界值.具体证明过程略.

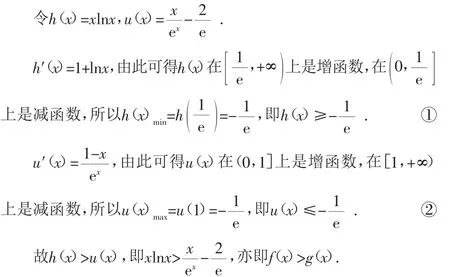
证明略，留给感兴趣的读者朋友去证明.

通过上述几道例题，我们可以看出，函数背景下的不等式证明对学生来说有两个主要的挑战：一是要善于观察待证不等式的等价不等式的结构特征，由等价不等式的结构特征去构造出相应的、适当的、合理的函数，将不等式证明的问题转化为对函数的有关性质研究的问题；二是要掌握有关函数性质研究的知识，掌握对有关函数性质研究的方法，积累对有关函数性质研究的经验.可以说，掌握好上述列举的三种类型问题的探究思维途径及思想方法，对函数背景下的不等式证明的问题就能很好解决了.