待定系数法在解题中的应用

☉浙江省诸暨市湄池中学 宋健红

对于某些数学问题，若得知所求结果具有某种确定的形式，则可研究和引入一些尚待确定的系数（或参数）来表示这样的结果，通过变形与比较，建立起含有待定字母系数（或参数）的方程（组），并求出相应字母系数（或参数）的值，进而使问题获解，这种方法称之为待定系数法.应用待定系数法解题的必要前提是正确判断解的形式结构，对此必须结合其他知识，其他方法综合考查.由于它的应用的广泛性和它在中学数学与高考中的突出作用，它已经成为一种重要的解题思想.

一、在不等式中的应用

分析：求函数的表达式，实际上就是确定系数m、n的值.

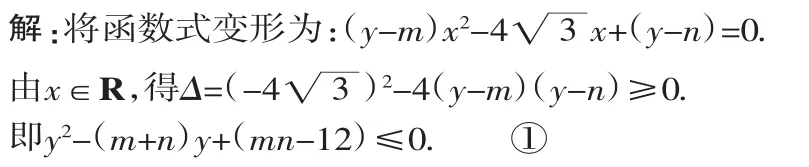
要使函数有最大值7，最小值-1，亦就是-1≤y≤7，显然（y+1）（y-7）≤0.

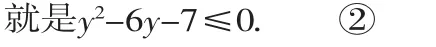
比较①、②的系数得方程组：

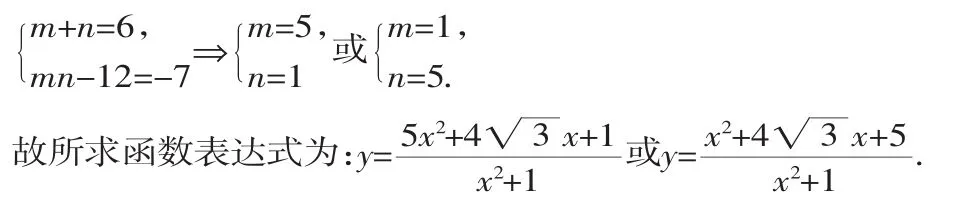
评注：从上述求解过程可以看出，待定系数法可以整体使用已知条件，简化运算过程，避免错解.

二、在数列中的应用

例2 是否存在这样的等差数列{an}，使它的首项为1，公差不为0，且其前3n项中，前n项的和与其后2n项的和的比值对于任意自然数都等于常数？若存在，求出数列{an}的通项公式及该常数；若不存在，说明理由.

解：设存在这样的等差数列{an}，其公差为d，前n项的和记为Sn，则其后2n项的和为S3n-Sn.

评注：有些数列问题，通过引入或研究一些尚待确定的系数转化命题结构，经过变形与比较，建立起含有待定字母系数的方程组，由此求出相应字母系数的值，进而使问题获解.

三、在三角中的应用

例3已知f（θ）=sin2θ+sin2（θ+α）+sin2（θ+β），其中α、β适合0≤α＜β≤π，试问：α、β取何值时，f（θ）的值恒为定值？

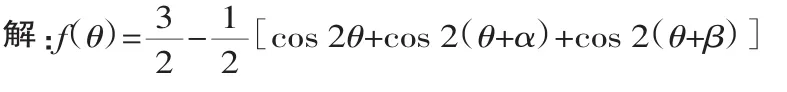
评注：对于恒为定值的三角函数求参问题，可以通过分离主变量，视主变量的系数为0，这样就可以求出参数值.

四、在圆锥曲线中的应用

解法1：因为椭圆的焦点位置不确定，故可考虑两种情形.（1）当椭圆的焦点在x轴上时，设椭圆的标准方程为：

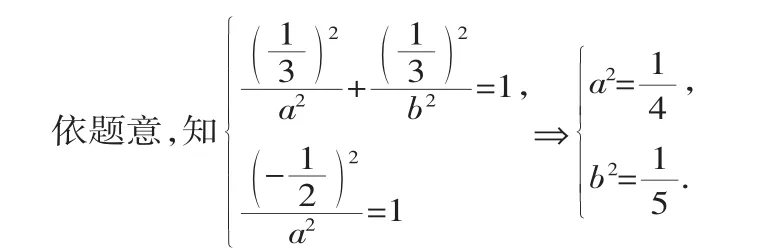
故所求椭圆的方程为4y2+5x2=1.

解法2：设所求椭圆的方程为Ay2+Bx2=1（A＞0，B＞0）.依题意，可得：

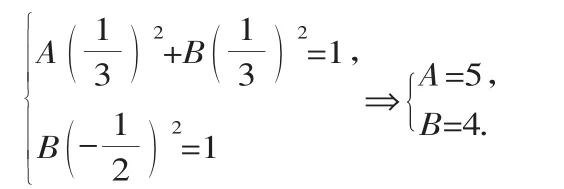
故所求椭圆的方程为4y2+5x2=1.

评注：确定椭圆的方程包括“定位”和“定量”两个方面.“定位”是指确定与坐标系的相对位置，在中心为原点的前提下，确定焦点位于哪条坐标轴上，以判断方程的形式；“定量”则是指确定a2、b2的具体值，常用待定系数法.