算法框图问题的几个切入点

☉河北省滦平县第一中学 张艳利 李连海

算法框图问题的几个切入点

☉河北省滦平县第一中学 张艳利 李连海

通过分析全国及各省市高考试题发现，算法问题的考查多集中在对程序框图的理解上，读懂图意是解题成功的关键.题型往往是选择题或填空题，难度较小，主要考查学生读图、识图、解图的能力和相关数学知识.下面就此类问题提出几点建议.

一、循环结构应重点掌握

在算法涉及的顺序结构、选择结构、循环结构这三种常见的结构中，高考命题以考查循环结构居多，因此应重点掌握.

例1 阅读如图1所示的程序框图，运行相应的程序，输出的结果S=_________.

解析：由程序框图可知：

第一次循环：a=1，S=0，n=1，S=S+a=1，a=a+2=3，n=1＜3满足判断条件，继续循环；

第二次循环：n=n+1=2，S=S+a=1+3=4，a=a+2=5，n=2＜3满足判断条件，继续循环；

第三次循环：n=n+1=3，S=S+a=4+5=9，a=a+2=7，n=3不满足判断条件，跳出循环，输出S的值.

综上，输出的S值为9.

点评：高考命题中多以考查考生阅读框图的能力为主，只要能读懂框图，就能顺利解答．本题考查程序框图及递推数列等知识.对于循环结构的输出问题，一步一步按规律写程序结果，仔细计算，一般不会出错，属于基础题.

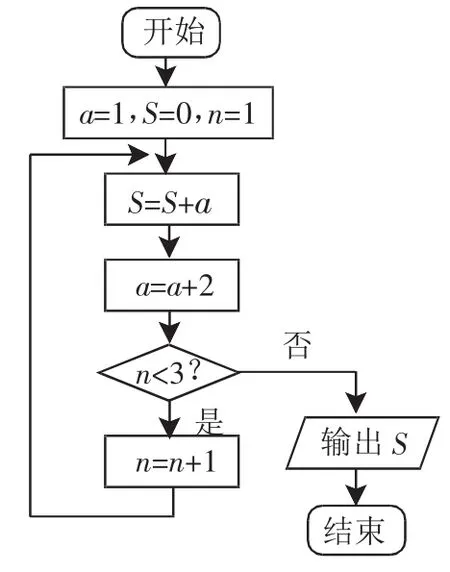
图1

二、与数列知识相结合的算法问题是重中之重

与数列知识相结合的问题是框图问题的重要形式之一，其中以等差或等比数列的求和尤为常见.

例2 如图2所示的程序框图输出的结果是________．

图2

点评：此类问题的解答，只要熟练等差、等比数列的求和公式，准确把握项数即可.

三、与函数的交汇常考常新

算法与框图因其内容单一，所以在高考中对此部分内容的考查与相关知识的交汇不可避免，其中与函数的交汇居多.

例3 图3为某算法的程序框图，则程序运行后输出的结果是________.

图3

解析：由程序框图可知：

点评：本题与函数相交汇，考查循环结构问题.解题的关键是确认何时循环终止，以体现考纲中要求理解输出语句、了解算法的含义与思想.

图4

四、条件的判断与结果的输出同等重要

解析：初始条件：S=0，n=2，i=1.

故选B.

点评：算法与框图问题的设问多以两种情况出现：一是输出结果的计算；二是循环条件的判定.因此教学中对这两种形式应同等重视.

总之，对于算法的考查重点是对程序框图各个步骤的理解，其中蕴含的数学内容往往不难.通法常常是使用代入法依次求出前几项，得出所需的结果或发现某种规律.一般来说，对于算法的考查实际上是“借算法之形”对其他数学知识点进行检测.故解答这一类题目不仅需要清楚了解算法的基本思想和结构，并注重与相关知识的交汇性.