重视数学课堂参与，提高教学有效性

☉江苏省江阴市长泾高级中学 孙福元

重视数学课堂参与，提高教学有效性

☉江苏省江阴市长泾高级中学 孙福元

富兰克林说：“告诉我，我会忘记；教给我，我可能记住；让我参与，我才能学会．”所以，要使学生真正地获得知识、发展智能、提高素质，就要采取合理的教学策略，让学生主动参与到课堂教学中来．而在目前的课堂中，很多教师的教学方式以“满堂灌”为主，找不到更有效的教学模式与方法，学生在课堂中消极等待思想严重，自主参与意识淡薄，如此教学效率低下的课堂既影响了学生的身心健康，又妨碍了学生的个性发展．针对以上问题，在教学实践中，就如何提高学生课堂参与度，笔者进行了如下探索．

一、设计情景引领，激发参与兴趣

孔子说：“知之者不如好知者，好知者不如乐之者．”兴趣是最好的老师，当学生对这门科目产生了兴趣之后，自然会学得比别人好．所以教师要特别注重课堂引入时情景的设置，可以寻找一些符合学生身心特点的、立意新、有趣味、构思独特的情景，通过情景的引领，激发学生的学习兴趣，提高学生参与课堂的热情．

案例1：在上“函数与方程”第一课时，笔者先给出以下图片（如图1）.

学生看了都很激动，议论纷纷，一会儿就有学生看出了这幅图中的奥妙：既可以看成两个人在对视，也可以看成一个酒杯，由关注的是白色还是黑色决定．从不同的角度看这些图，所看到的是不一样的景象，这与人的知觉选择性有关．由此，教师引出本节课所要学习的知识点：函数的零点，并和学生解释这其实就是以前所学的方程的根，一个是从函数的角度来研究，另一个是从方程的角度来研究的．这样，学生就很容易的理解了新的知识，也都很积极地参与到课堂之中，整节课学生都表现的很有激情，兴致盎然．

案例2：在讲《中心投影与平行投影》时，教师在上课时先用多媒体技术为学生播放生动、活泼的手影图《逗趣》和皮影戏《三只老鼠》，此前大多数学生会在电视中看过这种表演，所以学生看的很开心，特别当看见三只小老鼠互相调皮逗趣时，同学们更是看的乐不可支，教师随即提出问题：同学们，你们在感受这些小老鼠的调皮时，是否思考一下，这些图形形成的原理是什么呢？这些原理还有哪些重要用途呢？继而引出投影的定义．这样在创设轻松愉快学习情景的同时，让学生感受数学从生活中抽象出来的．

图1

以上两案例借助于多媒体技术，利用生动、直观的情境有效地激发联想思维，激发学生学习数学的兴趣与好奇心.通过共享多媒体信息，改变了传统教学中粉笔加黑板的单一、呆板的表现形式，增强了教学内容的表现形式，能将抽象、生涩、陌生的知识直观化、形象化，活跃课堂气氛，激发学生学习兴趣，加深巩固教学内容，使学生感受到学习的喜悦，调动了其主动学习的积极性，多媒体技术在贯彻教学的直观性原则上发挥了其独特的优势．情境认知理论认为：“情境是学习发生与进行的必要条件，而且情境具有线索指引的功能，有助于学习知识的保留．”教师要善于结合教材内容和学生的实际状况，选择贴近生活实际的或者有趣味性的问题情景进行导入，以此激发学生学习和探究的兴趣，学生的课堂参与度将会有很大的提高．

二、重视动手操作，亲历知识形成

笔者多年的教学实践表明：数学课若一味地讲授，学生很容易产生抽象乏味的感觉，从而产生厌学情绪并养成惰性．因此在教学过程中，教师应尽可能地创设各种动手操作的情景，优化教学手段，让抽象的数学知识更加形象具体．通过动手操作，使学生亲身感受知识的形成过程，激励学生去努力成为一个发现者、研究者、探索者，使学生的心理活动处于积极主动地学习状态，这样不仅提高了学生学习数学的兴趣，而且可以使学生更牢固地掌握知识．

整节课上学生都在积极地动手、动嘴、动脑，这部分活动的安排，主要体现了数学知识的产生和发展过程，也体现了数学的应用价值，提高了学生分析问题、解决问题的能力.动手操作是一种发展学生思维和创新能力的重要教学活动，是让学生主动探索，获取知识的重要方法.在数学教学中，应重视通过观察、操作、猜测等方式，培养学生的主动参与意识和勇于探索的学习能力，让学生去体验数学知识的形成过程，从而使学生对知识的理解将更加深刻.

三、关注个性差异，实施分层教学

目前我们一个班级的教学对象一般50人左右，学生的知识基础、智力水平、学习能力有着很大的差异，如果对每个学生的训练都同一标准，则必然是优秀者兴趣过剩，学困生畏难扫兴.所以在教学中，教师应该针对教学内容，关注不同层次的学生，实施分层教学.让不同认知水平的学生从自身实际出发，有适合自己的内容可听，有题可做，从而促使不同层次的学生都参与到课堂中来，通过自己的智力活动提高运用知识的能力.

首先，在课堂提问上，要关注个体差异.教师应该根据学生身心发展和课程学习的特点，给每一个学生提供思考、创造、表现及成功的机会，设置不同层次的问题给不同层次的学生，让学生觉得自己可以在课堂上回答出问题来，就有了学习的动力.

其次，在课堂练习上，要改变“一刀切”的模式.教师可根据学生数学已有水平及智能结构的独特性，将学生分成“学困生、中等生、学优生”三层，依据学生分层情况匹配每一层的练习题，从而满足不同层次学生的需要，让不同的学生能获得不同的需要，使不同个体活力得以彰显.

案例4：向量数量积的概念教学之后，可设置以下三个课堂练习题.

让三个层次的学生各选对应的（1）、（2）、（3）题做，学困生在做好题（1）后，也可以去尝试做题（2），这样让每个学生都有自我表现的机会，有“够得着”的成就感.

另外在布置课后作业时也要注意学生的层次，客观看待学生身上的差异，采取分层练习的方式，使每个学生在自己原有的基础上得到最优发展，真正让作业对每个学生都适合并且发挥其最大的效益，教师在课堂中还要注意维护学生的人格尊严，宽容学生的缺点和错误，以发展的眼光看待学生，及时赞赏学生所取得的任何进步，充分肯定学生的成长和发展，这样才能使学生的参与意识得以持久，给每个学生成功的喜悦.

四、挑起认知冲突，强化参与动机

学生的参与欲望是一个不容忽视的因素，而学生的认知冲突是学生学习动机的源泉，也是学生积极参与思维学习的原因.所以，教师在教学中要不断设置认知冲突，锻炼学生思维，提高学生的认知水平，激发学生的参与欲望.让学生带着疑惑去探究，他们参与课堂的积极性无疑会更加高涨，从而强化参与动机.

案例5：已知函数f（x）=x3－3x，过点P（2，－6）作曲线S：y=f（x）的切线，求切线方程.

生1：由f′（x）=3x2－3，求得过点P的切线斜率k=f′（2）=9，再由点斜式得直线方程，得过点P的曲线S的切线方程为y=9x－24.

师：是否可从图像直观分析出我们需要进一步考虑其他因素呢？（这时有部分学生在画图，作好图（如图2）他们举手提问）

生2：老师，点P（2，－6）不在曲线y=f（x）啊，上述方法是点P在曲线上的求切线方法，正确吗？

这时刚才算的不亦乐乎的同学恍然大悟：是的啊，我怎么没想到呢，那肯定有问题，应该怎么做呢？教师就此引导学生分析，以前我们都是利用导数的几何意义，求在某点处的切线.在此题中，点P恰恰不在曲线S上，求过点P的切线方程，这两个问题该如何区分呢？通过学生热烈的讨论，同学慢慢理解了过点P的切线，只是说明切线经过点P，切点很有可能就不是点P，然后教师再鼓励学生探索该如何求解，学生想到应该先设切点，得出切线方程，然后将点P代入即可求解.

通过上述解法的不断深入求解，学生思维被调动起来，当这几个问题解决后，整个解题过程清晰明了，问题也就迎刃而解了.通过这样设计，层层深入，不断设置认知冲突，使学生始终处于一个不断发现问题和解决问题的过程之中，有助于激发学生的求知欲望和参与动机.

北京师范大学曹才翰教授指出：“数学学习是再创造再发现的过程，必须要主体的积极参与才能实现这个过程.”因此，教师应该时时注意学生在课堂上的参与情况，及时帮助那些在课堂上参与程度不高的同学，充分调动学生学习的自觉性和积极性，从而培养学生课堂参与意识，引领学生努力探索，不断创新，以激发其学习热情，让所有的学生都积极参与到课堂中来.

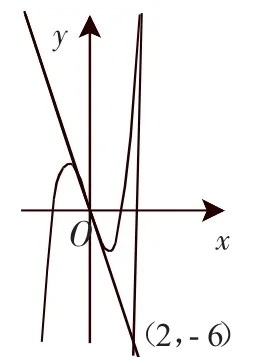
图2

1.周智才．论培养学生课堂参与意识的途径［J］．科技信息（科学教研），2009，7.

2.郑烨.谈提高中数学课堂中学生参与度的方法［J］.学科教学，2009，7.