对数不等式的源与流

☉浙江省温州中学 林庆望

对数不等式的源与流

☉浙江省温州中学 林庆望

含对数的不等式常用构造函数求导数的方法证明，但这种方法并不是放之四海而皆准的，有时会遇到导数越求越麻烦的情况，使思路陷入僵局.下面介绍一个基本对数不等式，用它可以证明一些含有对数的不等式问题，以此说明它在解决含对数不等式问题中的优越之处.

一、基本对数不等式

评注：对于ln（1+x）＜x，从几何意义上来说，y=x为y=ln（1+x）在x=0处的切线方程， 即当x＞－1时，函数y=ln（1+x）的切线图像始终在y=ln（1+x）的图像上方.如图1所示.

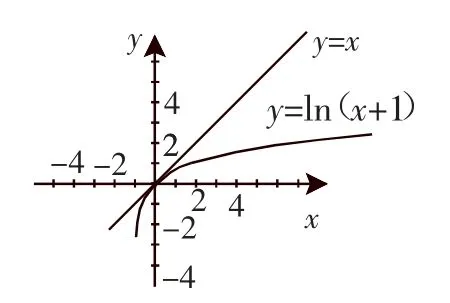
图1

二、应用举例

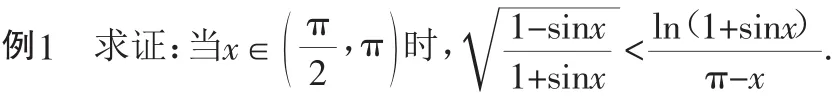
证明：令t=π－x，原不等式等价于：

评注：第（2）问中先分析结论an＜e2，两边取对数后原问题相当于要证明lnan＜2，而原题中给出的是an与an+1的递推关系式，因此想到采用“插项”的手法来证明（lnan－lnan－1）+（lnan－1－lnan－2）+…+（lna2－lna1）+lna1＜2，而这里的关键是要用到第（1）问的结论和ln（1+x）＜x.

例3（2010年全国卷一理20）已知函数f（x）=（x+1）lnx－x+1.

（1）若xf′（x）≤x2+ax+1，求a的取值范围.

（2）证明：（x－1）f（x）≥0.

证明：（1）略.

（2）由基本对数不等式ln（1+x）＜x，可得lnx≤x－1.

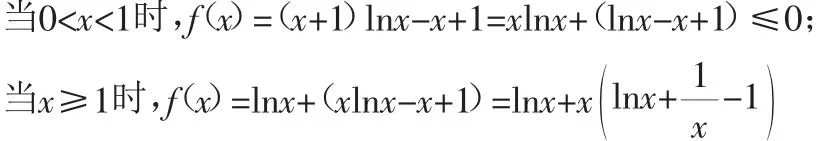
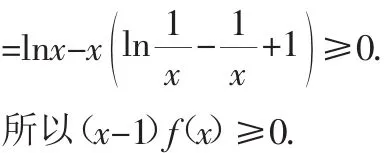
评注：第（2）问采用“分解”的眼光将原不等式的证明转化为对f（x）符号的讨论，分0＜x＜1和x≥1进行讨论，而这里f（x）符号的确定是ln（1+x）＜x这一不等式在起关键作用.