为学生的思维打开一扇窗

☉江苏省东海县青湖中学 高桂霞

为学生的思维打开一扇窗

☉江苏省东海县青湖中学 高桂霞

数学教学的目的之一是培养学生的思维品质，提高学生的思维能力，使学生在学习数学基础知识的同时，不断发现数学的思维过程，学到其思维方法，从而学会独立探索，有所发现，有所创新，以便更好地掌握和应用知识．数学思维训练通常是以解题教学为中心展开的．没有一定量的题练，固然达不到练就过硬解题本领的要求，但“题海之战”也未必培养出高素质、高能力的学生，反而加重他们的负担，带来负面影响，这与素质教育是相悖的．

一、一题多练，拓展思维空间

集中思维通常称为求同思维，主要是依靠已有的知识体系，展示现成解决方案和答案的一种思维方式． 根据集中思维的特点，如果给出一道题不变换其意境，使学生在领会题意的基础上，发挥记忆和合乎逻辑的推理功能，可以拓展学生的集中思维空间． 一题多练是训练学生拓展集中思维的有效方法，从中可以进行同中求异，异中求同的思维训练，达到触一题，通一类之功效．

例1 根据下列条件，求出抛物线的解析式.

适当处理以上例题，可以拓展学生数学学习的思维空间，给他们以较大的思想范围，并引导学生根据已有的知识、经验和方法，对数学问题广泛联想，积极探索，不“墨守成规”，追求“标新立异”.

二、一题多解，拓展发散思维空间

数学教学不仅要准确地传授知识，而且也要注意对学生的思维加强训练，尤其是发散思维训练.训练发散思维，着眼于探索未知事物，鼓励学生大胆地去追求事物间的新关系，解决问题的新方法，寻找问题的新答案.

不少习题，有多种解法，因而解完一道题后，应反思一下是否还有更好的解题途径.这样既能加强知识间的联系，又培养了学生周密的思考能力.

例2 如图1，在△ABC中，∠BAC=90°，AB=AC，D为AC的中点，AE⊥BD，垂足为E点，延长AE交BC于F.求证：∠ADB=∠CDF.

分析1：证明两个角相等，首先考虑证两个三角形全等.由于∠ADB在△ABD中，故可设法构造一个与△ABD全等的三角形，并使这个三角形中含有一个锐角等于∠CDF.

解法1：过点C作AB的平行线与AF的延长线相交于点H.

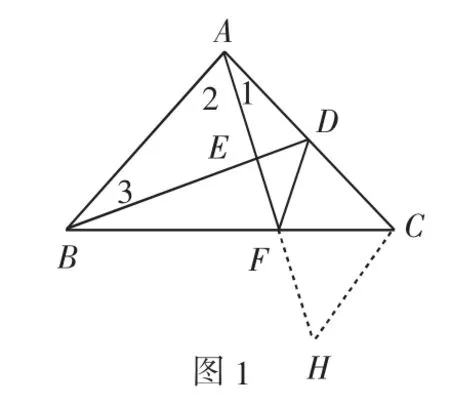
分析2：从另一个角度分析.因为∠CDF在△CDF中，并有条件AD=DC，故可设法构造一个与△CDF全等的三角形.考虑到∠C=45°，所以可作∠BAC的平分线AM.

解法2：如图2，过点A作∠BAC的平分线AM交BD于M.

因为∠BAC=90°，

所以∠DAM=∠BAM=45°.

因为AE⊥BD，

所以∠BAE+∠3=90°.

又∠1+∠BAE=90°，所以∠1=∠3.

因为∠BAC=90°，所以AB=AC.

所以∠C=45°，所以∠DAM=∠BAM=∠C.

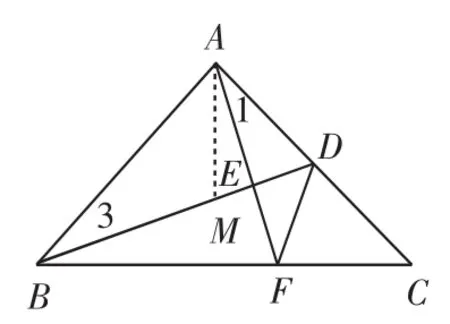
图2

在一题多解后，可分析各种解法的合理性，用对比的方法，选出最佳解（证）法.从而不仅拓展了学生的解题思路，而且培养了他们的创新意识，开拓了学生的发散思维的空间.

三、一题多变，是发散思维与集中思维相互转化的两个方面

一个创造思维活动的过程，要经过从发散思维到集中思维，再从集中思维到发散思维多次循环才能完成.在创造思维品质的发展中，发散思维和集中思维中思维处在不同的地位，起着不同的作用.所以教师在培养学生集中思维的同时，必须重视发散思维的训练，因此可提供一些一题多变的题目，使学生在寻求各种结果中，表现思维的创造性.

上面的例2，我们可以把原题的条件和结论交换一下，得到下题：

例3 在△ABC中，∠BAC=90°，AB=AC，D为AC的中点，点F在BC上，∠ADB=∠CDF，连接AF交BD与E.求证：AF⊥BD.

分析：证明两线段垂直，只需证明交角是90°.因为这个角在△ABE中，所以只要证明∠EAB+∠EBA=90°，而题中∠1+∠EAB=90°，所以只要证∠1=∠3即可.

证明：如图2，过点A作∠BAC的平分线交BD于M.

又因为∠1+∠BAE=90°，所以∠3+∠BAE=90°，所以∠AEB=90°，即AF⊥BD.

总之，数学解题教学中，应就题目的目标、内容、结构、特征等采用一题多解、多题一解、一题多变、一题多用、一题多联，进行不同方面、不同角度、不同层次的分析、探索，其效果必胜于“宁多勿缺”的大运动量的机械重复.