课堂中暴露思维过程是数学教学的灵魂

☉江苏省南通中学 杨建楠

课堂中暴露思维过程是数学教学的灵魂

☉江苏省南通中学 杨建楠

一、什么是课堂中的暴露思维过程

数学课堂中暴露思维过程指：在课堂中向学生展示数学家的思维、教师的思维以及学生的思维三种思维活动.具体地说，就是将知识的形成过程、结论的探索过程、问题的深化过程、分析问题和解决问题的过程展现出来.数学教学大纲指出：“数学教学中，发展思维能力是培养能力的核心.”“数学的学习过程不仅是知识的接收、贮存和应用的过程，更重要的是思维的训练和发展过程.”在课堂上暴露思维过程，是为了潜移默化地培养学生的数学能力，数学是思维的体操，数学课堂以思维的训练和发展为主线与目标，而思维的训练和发展又是以暴露思维过程为前提的，数学能力是在暴露思维的过程中得到锤炼和提高的.数学课堂活动中，师生双方都应该充分暴露思维过程，一方面：教师将教材安排的意图，自己处理问题的想法表现出来，展现给学生，便于学生深层次的理解与思维方法的借鉴；另一方面：学生将自己对问题的认识，如何思考与研究问题的思维过程暴露出来，便于教师及时反馈评价与有针对性的纠错.这样数学课堂活动就沟通了师生间思维路线，形成“教”与“学”的回路，这样的数学教学才有助于优化学生的思维品质，发展学生的思维能力，因此可见课堂中暴露思维过程是数学教学的灵魂．

二、课堂教学中暴露思维过程的原则

暴露数学思维过程的目的是使学生在原有知识和经验的基础上，在主动参与中，通过操作与实践，由外部活动逐渐内化，完成知识的发展过程和“获取”过程，突破学生思维障碍，所以在数学教学中，暴露思维发生发展过程是符合学生认识规律的．暴露数学思维过程教学中要坚持：（1）主体性原则，课堂教学中，要求体现学生是思维活动的主体．遵循学生的思维规律，课堂教学活动中要求教师与学生的思维同步，必须按照思维活动过程的规律进行教学，使学生能形成良好的认知结构，优化的思维品质．（2）对应性原则，课堂教学中，要注意二个方面的对应，一是暴露思维过程应当与教材结构和教学内容相对应，二是必须要围绕着教学难点去分析和设计暴露的程序与思考的对策．（3）启发性原则，课堂教学中，要尊重学生的思维特点，不能置学生的心理状态和思维状态于不顾，超前指路，也不可强制学生按自己提出的途径和方法去思考问题，越俎代庖选取优化的启发策略，课堂活动中当学生思维受阻时，教师应遵循学生思维的途径和规律启发学生，应当善于因势利导、层层设疑、步步深入，朝着有利于学生思维发展的方向去启发与引导．（4）过渡性原则，课堂教学中，暴露思维过程要适时、恰当，把握好“过渡”契机，使得课堂教学中的暴露过程具有“过渡”的合理性．（5）双方性原则，课堂教学中，思维的暴露不仅仅是一方面的，它必须是师生双方共同在教学活动中充分暴露思维的一个过程．

三、课堂教学中暴露思维过程的时机

1．在探索中暴露

教材因为篇幅的关系许多内容省略了知识的发展、探索过程，数学中的定理性质是如何发现的，解决问题的方法是如何构想的和研究的，学生对它们的发现和探索过程有种神秘感和疑惑感．在课堂活动中，教师去模拟知识形成的原始思维，暴露探索知识的过程，为学生创设问题情景，教会学生去发现问题与研究问题的思维方式以及方法．

2．在反思中暴露

学生在学习数学过程中，往往注重数学的结论，轻视获得结论的思维过程中，轻视反思问题，轻视深化知识的过程．而学习中的反思是思维发展的重要手段，所以在课堂活动中要善于去启发、引导学生去反思思维过程，以达到暴露思维的目的．

案例2：以原点O和点A（5，2）为顶点作等腰Rt△OAB使∠B=90°，求点B的坐标．

由于解析几何的思维习惯性，学生意识不到向量方法的应用，这三种方法的层层推进，计算的优化只是表象，思维的变化才具有更多的价值．

3．在延伸中暴露

教师指导学生解题、证题，常有这种现象，题解完了，但学生的思维过程并没有结束，教师若能抓住这个理想的思维机会，把学生想要延伸或想要表达出的的思维过程揭示出来，这不仅仅拓宽了思维空间，延长了思维的时间，而且加大了思维的力度，促使了思维的“上升”．例如：解后审视解题过程，评价原认识过程，检查解题过程是否准确，讨论或论证是否严密，方法是否恰当，有没有更简捷更高明的方法，对所得的结果能否进一步引申推广，能否总结出规律来等等，通过延伸思维引导学生自我总结和领悟解题中的数学思维与数学方法，积累对数学知识联系的整体感知，

案例3：解析几何复习课.

例题 已知：点P在椭圆x2+4y2=4上运动，求定点A（0，2）到动点P的距离AP的最大值．（讲解完以后，师生共同对问题的条件、结论等进行改变以及拓展）

变题1：将求AP的最大值改为求AP的最小值．

变题2：将椭圆改为双曲线x2－4y2=4，结论改为求AP的最小值．

变题3：将椭圆改为抛物线y2=2x，结论改为求AP的最小值．

变题4：已知点P在椭圆x2+4y2=4上运动，定点A（0，a）（a＞0），求AP的最大值．

变题5：动点Q在圆x2+y2－4y+3=0上运动，动点P在椭圆x2+4y2=4上运动，求PQ的最大值．

变题6：求三角式（cosα－2cosβ）2+（2+sinα－sinβ）2的最大值．

4．在铺垫中暴露

数学解题教学是数学教学的重要手段，因此教师在解题时要充分暴露思维的过程．解题方法的优劣、速度的快慢都取决于思维能力的高低，而思维的提高与发展又依赖于解题过程中所创设的问题情景，所以解题教学中暴露思维过程是培养思维能力的良田沃土．一般来说，综合性能愈强，知识跨度愈大的数学题，要求解题的思维层次愈高、方法的技巧性愈熟练，思维训练的价值愈大，学生就愈难以理解．这就要教师精心设计，做好中介铺垫，减小问题的坡度，从未知顺利的引渡到已知．铺垫思维暴露，就是把架桥铺路的思维过程暴露出来，给学生架起思维的“梯子”，促使学生思维上“台阶”．

案例4：由数列递推关系求数列通项.

例题 已知数列{an}中，a1=1，an+1=an+1，求通项an．

（学生齐声）：因为an+1－an=1，所以{an}是等差数列，所以an=1+（n－1）·1=n．

T：很好．若将an+1=an+1改为［变式1］an+1=an+2n－1，此时由an+1－an=2n－1推不出{an}是等差数列，我们如何去求解？

T：（启发）思维受阻时不妨“特殊探路”——譬如求a4．

S2：a2－a1=1，①⇒a2=2，a3－a2=2，②⇒a3=4，a4－a3=4，③⇒a4=8．

T：那么求a100呢？难道也是这样一项一项求？能否直接求出a4呢？

S3：有了，只要把①、②、③式相加即得a4－a1=1+2+4，所以a4=8．

T：对，这叫做“设而不求”，这个解法我们取名为“累加法”．现在你们会求an了吗？

学生很快地求出了an=2n－1．

T：那位同学能对上述问题做一个小结．

S4：形如an+1=an+f（n）的递推关系式，常用累加法转化为等差（比）数列求和．（T：我们把这样的方法叫做累加法）

T：下面，再将an+1=an+2n－1变为［变式2］an+1=an·2n－1怎么求an？

S5：类比［变式1］的解法我们可以知道可以用累乘法

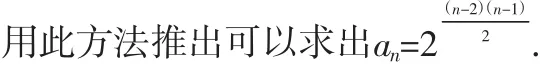
T：你能给这样的题型做一个小结吗？

S5：形如an+1=an·f（n）的递推关系，常用累乘法求通项．

T：再将前面问题中的an+1=an+1改为［变式3］an+1=2an+1（其他不变），如何求an？

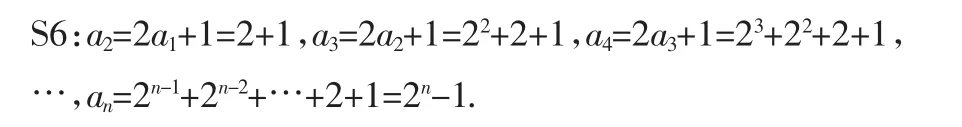
T：很好，答案正确，但这仅仅是猜想，还需要用数学归纳法加以证明．这也是一种方法，这叫“先猜后证法”．请大家思考有无更简便的方法？能否转化为等差（比）数列？{an}本身是等差（比）数列吗？

n+1n数）．

T：很好，他们由an+1=2an+1能转化成一个复合型{an+c}，然后说明复合型{an+c}是等比数列，an就可求了，能把这一方法推广到一般性？

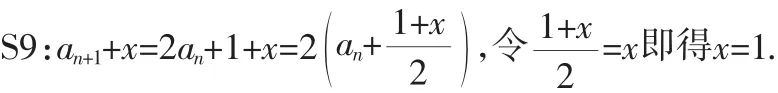
5．在设计中暴露

课堂教学中精心设计的诊断性题目，通过题目的设计达到暴露思维的目的．如何设计好有诊断性的题目呢？首先要了解学情：了解学生可能产生的错误想法，设计在学生思维和方法上容易出错的地方设计，其次在实施过程中，要使学生的观点充分暴露后，再提出矛盾，抓住它做剖析治理．从暴露学生失误思维入手，启发学生自悟、自救．面对学生的失误不要过早的点明，而应在暴露学生思维失误的过程中，让学生自我发现，在教师的正确思维的引导下自我纠正．

6．在讨论中暴露

在课堂教学中，为了充分的暴露学生的思维过程，在教学中教师要有意识的设置疑难，有组织的展开讨论，把疑难问题引人深思，常常选择一些学生不易理解的概念，不能正确运用的知识或容易混淆的问题让学生讨论，从错误中引出正确的结论，给学生留下深刻的印象．

7．在细微中暴露

课堂教学中教学中，有许多细微部分往往具有十分丰富的思想内含，存在着很大的思维训练价值，因此在教学活动中教师要善于“小题大做”，促使在“细微”中充分暴露思维过程．例如：在等比数列求和公式教学中，教会学生识记、应用公式固然重要，但更重要的是推导公式过程中所涉及的思维方法和求数列前n项和的思维策略．所以讲授时对公式的推导过程应采用慢镜头的思维剖析，挖掘“错位相减法”的思维过程，为后面学习数列求和打下了坚实的基础．讲指数函数、对数函数概念时，应暴露底数a范围规定的原因，强调a的区域，通过“假设”反问，反复暴露，反复强刺激学生，给学生留下深刻印象，为后面研究其性质埋下伏笔．对教材细微之处的挖掘有助于学生的进一步学习，有利于培养学生思维的深刻性和严密性．

1．薛茂芳．数学概念及其教学［M］.郑州：河南教育出版社，1994．

2．涂荣豹．谈提高对数学教学的认识［J］.中学数学教学参考，2006（1-2）．

3．吴松娇．浅析高中生数学思维障碍［J］．中国科教创新导刊，2008（21）．