一道《中学数学》“新题征展”题的探究

☉甘肃省天水市第一中学 宫前长

一道《中学数学》“新题征展”题的探究

☉甘肃省天水市第一中学 宫前长

一、问题提出

《中学数学》杂志2010年第3期（上）的“新题征展”（113）中的一道创新应用题：

如图1，设P是⊙O：x2+y2=2上的一点，定点A（－1，0），过原点O作直线PA的垂线交直线x=－2于Q点.

（1）若点P的坐标为（1，1），求证：直线PQ与圆O相切.

（2）试探究：当点P在⊙O上运动时（除去圆与x轴的交点），直线PQ与⊙O是否保持相切的位置关系？若是，请证明；若不是，请说明理由.

题目特点：题目是以圆的标准方程给出，“定点”的出现与“直线PQ与⊙O是否保持相切的位置关系”的出现，给题目增加了亮点.第二问又以存在性问题的形式展示，进一步增强了题目的可读性与探究的魅力，步步为营，层层诱导解题者坚定信心，促使持之以恒地进行探究，是一道考查直线与圆的位置关系的好题.

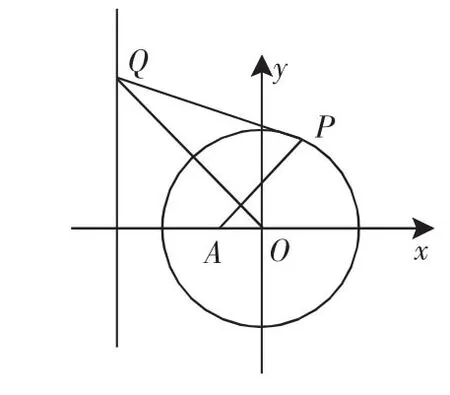
图1

二、问题探究

1.解法赏析

又kPQ·kOP=-1，所以PQ⊥OP.故直线PQ始终与⊙O相切.

点评：上述解法是通性通法，自然具有一般性，有利于对本题进一步的探究.

2.剖析原题的“数”与“形”的关系

经过认真的思考，以逆向思维的方式将题目的“结构”与“数据”中潜藏的关系显化出来，其思考的过程是：

从题目的“结构”（包含图形）看，题中有“直线PQ与⊙O是否保持相切的位置关系”的结构，图形中出现“双垂直图”（PQ⊥OP与PA⊥OQ）的结构；从题目的“数据”（包含等式）看，题中有“⊙O的方程：x2+y2=2”、“定点A（－1，0）”、“直线x=－2”的数据，解法中可归纳出斜率等式：kPQ·kOP=kPA·kOQ=－1.这些结论的出现，就会启发对此题的进一步思考.

反思：从上述题解题过程中，凭直觉思维和对此题的感悟，通过反思题意和解题过程，提出问题：对所涉及的定点与给定的直线之间是否存在什么关系？定点、直线与圆之间是否也有某种关系？能否将其进一步一般化？等等.

感悟：从解决问题的特殊性进行思考：既然“直线PQ始终与⊙O相切”，自然就会将问题特殊化，过定点A（－1，0）作x轴的垂线与圆的交点的坐标为（-1，1），其切线方程是：－x+y=2，这时令y=0，就会得到切线与x轴的交点的横坐标是－2，结合题目可知，此－2应该是题目给出的直线x=－2与x轴的交点的横坐标.这就说明，定点与给出的直线方程之间是有一定联系，而且也与圆之间存在一定的关系.依据上述的剖析和解法，可以将其第二问进一步一般化.

3.原题的探究——变式设计

思路：当点P在⊙O上运动时，直线PQ与⊙O保持相切，只需证明出kPQ·kOP=－1，或直线PQ的斜率与⊙O上在点P处切线的斜率相同即可.

综合变式1、2，可以得到下面结论

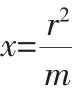
三、原题的推广——类比设计

大家知道，圆中的许多性质可以通过类比到椭圆、双曲线中仍然是正确的，为此，对原题的条件进行适当地改变，从而得到椭圆中的类似问题.

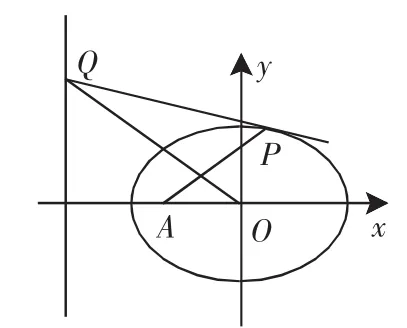
图2

思路：当点P在椭圆上运动时（除去椭圆与x轴的交点），直线PQ与椭圆始终保持相切的位置关系，只需要说明椭圆在点P的切线与直线x=－的交点Q恰好与原点O的连线经过直线PA被椭圆所截弦的中点即可.

1.宫前长.考题无独有偶理念蕴藏厚重［J］.中国数学教育（高中版），2011（4）：24-27.