合情化归 探求创新试题

☉江苏省阜宁中学 丁敏春

合情化归 探求创新试题

☉江苏省阜宁中学 丁敏春

由于创新试题有很好的区分和选拔功能，所以在2012年高考数学试题中具有创新意识和创新思维的新题精彩纷呈.数学创新试题具有以下鲜明的特点：背景新颖，内涵丰富，数学本质深刻，设问方式灵活等.高考数学创新试题主要题型有：（1）新定义型试题；（2）图形信息型试题；（3）实际应用型试题；（4）类比归纳型试题；（5）综合知识型试题；（6）能力探究型试题.本文尝试运用合情化归探求解答2012年高考中的部分数学创新试题.

所谓“化归”，就是转化和归纳.在解决数学问题时，人们常常将待解决的问题甲，通过某种转化过程，归结为一个已经解决或者比较容易解决的问题乙，然后通过问题乙的解答返回去求得问题甲的解答.化归就是问题的规范化和模式化.

一、化归的基本要素

（1）化归对象；（2）化归目标；（3）化归途径.

二、化归的基本原则

1.熟悉化原则

将待解决的陌生问题化归为一个比较熟悉的问题，就可以充分调动已知的知识和经验运用于面临的新问题，从而有利于问题的解决.

2.简单化原则

将一个复杂的问题化归为一系列比较简单的问题，可以通过分类、割补、特殊化、换元等具体方法使问题变得简单.

例 （2012·新课标理·11）已知三棱锥S－ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC=2，则此棱锥的体积为（ ）。

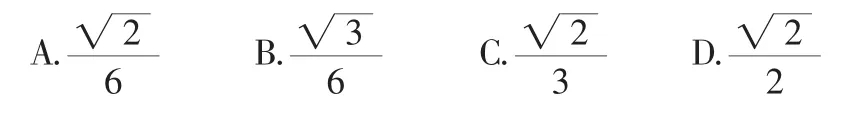
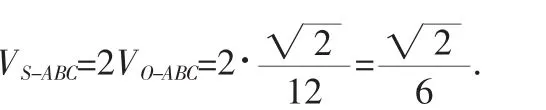
3.直观化原则

具体化就是把比较抽象的问题转化为比较具体直观的问题，以便形象地把握问题涉及的各个对象之间的关系.

A.当a＜0时，x1+x2＜0，y1+y2＞0 B.当a＜0时，x1+x2＞0，y1+y2＜0 C.当a＞0时，x1+x2＜0，y1+y2＜0 D.当a＞0时，x1+x2＞0，y1+y2＞0分析：先绘画四图：

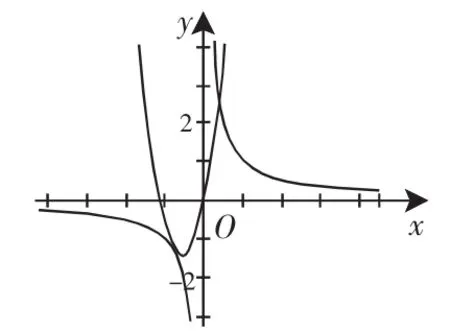
图1

图2

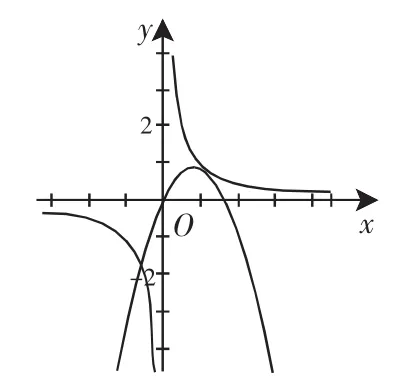
图3

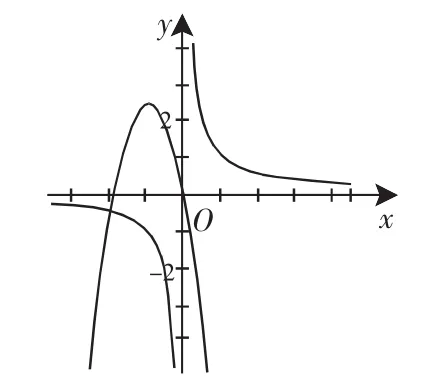
图4

观察图1（当a＞0，b＞0时），图3（当a＜0，b＞0时），两个图像各有两个不同的公共点.

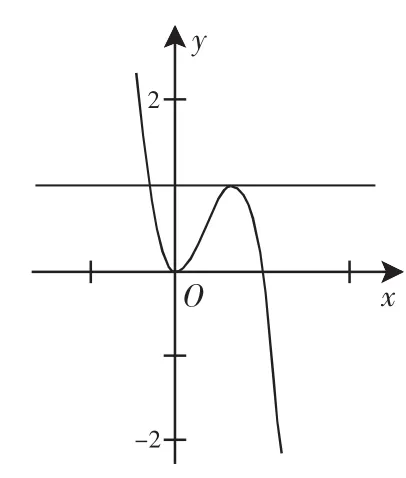
图5

由φ（x）x=1，推得4b3=27a3.

故答案为B.

4.本源化原则

我们应善于从数学问题的条件和结论中概括出问题所蕴含的数学知识、数学思想，回归数学问题的源泉和本质.

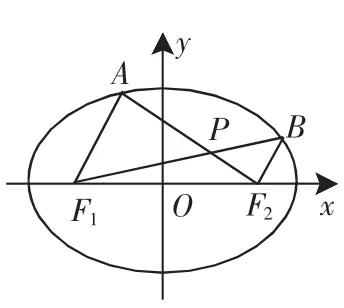
图6

设A，B是椭圆上位于x轴上方的两点，且直线AF1与直线BF2平行，AF2与BF1交于点P.

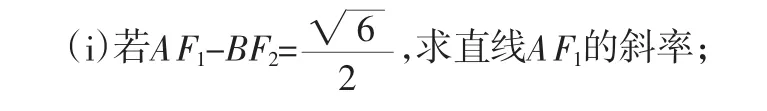
（ii）求证：PF1+PF2是定值.

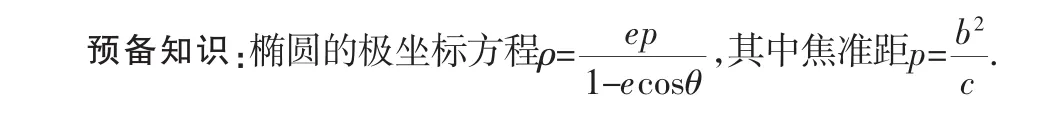
如图7，设∠xF1A=θ，C点极角为π+θ.

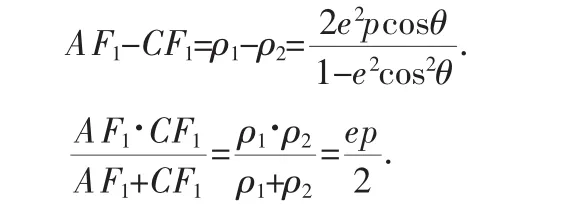
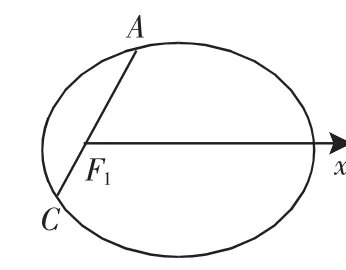
图7

化归：设点C与B关于原点O中心对称，由条件AF1平行于BF2，知A，F1，C三点共线，且CF1与BF2平行且相等.

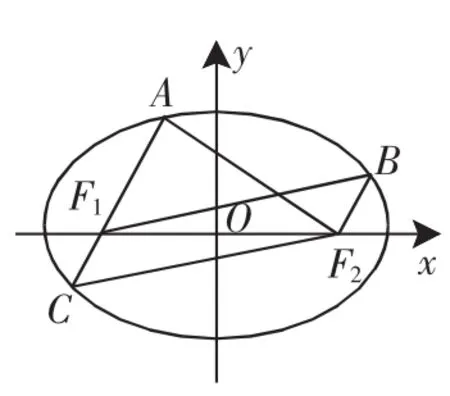
图8

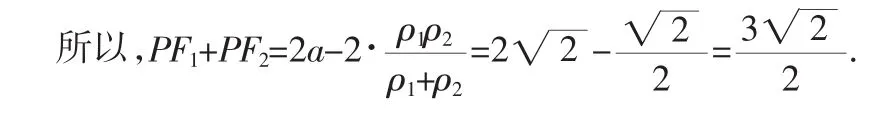
5.和谐化原则

这里的“和谐”是指对偶与匀称，是指把条件和结论的表现形式转化为更具有数与形内部固有的和谐统一的特征.

观测横轴：求解二元变量的取值范围常用方法.

观测纵轴：线性规划知识.

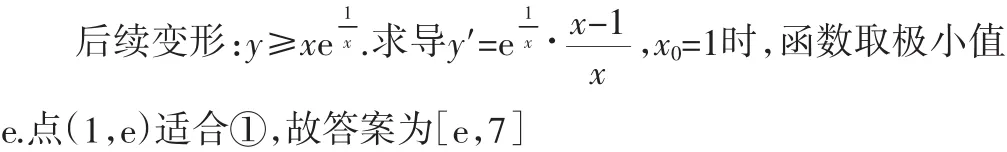
6.正难则反原则

当正面讨论问题遇到困难时，可设法从问题的反面去探求，使问题获得解答.如反证法，求参数范围时的补集思想，概率问题中的对立事件等.

三、化归的基本途径

1.等价转化

将原题转化为与之等价的命题.

例（2012·北京理·14）已知f（x）=m（x－2m）（x+m+3），g（x）=2x－2，若同时满足条件：

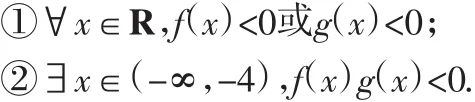
则m的取值范围是_______.

分析：①p∨q为真等价于p，q有一真，所以，当∀x∈［1，+∞）时，f（x）＜0；

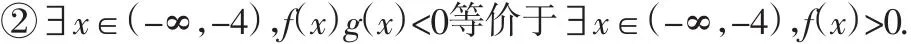
结合二次函数图像，列式f（1）＜0，f（－4）＞0，解得－4＜m＜－2.

2.数形结合

将问题中的数量关系（解析式）与空间形式（图形）关系互相转化.

3.退化处理

常用的方法为降元降维降幂.

4.构造法

“构造”一个合适的数学模型.

总之，解题者的“兵力”是数学基础知识，解题者的“兵器”是数学基本方法.成功解题的基本要素是：知识结构，思维能力，经验题感，情感态度.化归是解决数学问题的一种重要思想方法，善于使用化归是数学思维方式的一个重要特点.合情化归是有效解题的强力引擎，我们期待合情化归一定会创造更多数学文化价值.

1.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，1997.

2.赵小云，著.数学化归思维论［M］.叶立军，译.北京：科学出版社，2006.