相似三角形等积式问题证明“三部曲”

☉广东省深圳市南山区第二外国语学校 何小波

等积式证明问题是初中平面几何的重要内容，它涉及的知识内容广泛，有利于培养学生综合运用知识的能力.等积问题综合性强，类型繁多，涉及面广，难度大，加之许多学生由于基础知识不牢，不善于归纳总结，结果在解决等积问题时不能灵活运用，感觉问题的分析困难，甚至是无从下手，望而生畏.为此，笔者总结提出了等积式问题证明的“三步曲”.所谓“三步曲”是指在证明等积问题时，首先考虑把等积问题化为等比问题，然后证明相关的三角形相似.其次，在无法证明三角形相似时，可用问题中所蕴含的与等比中某一线段相等的线段或相等的比值来代替.最后，若无法找到相应的等线段或等比时则通过平行线成比例线段这一相关性质找相应的比值.下面结合一些具体的实例进行分析.

1.等积式化比例式，横找竖找找相似

遇到等积问题时，首先把等积化为等比的形式，然后考虑证明两个三角形相似.

例1 如图1所示，在△ABC中，高线AD、CE交于点O.求证：OC·BD=AB·OD.

证明：因为AD，CE是△ABC的高线，

所以∠EAO+∠AOE=∠DCO+∠COD.

因为∠AOE=∠COD，

所以∠EAO=∠DCO.

因为∠ADB=∠ODC，

所以△OCD∽△BAD.

评注：由于比例的性质——比例的内项或外项可以交换位置，所以在根据比例式寻找相应的相似三角形时，需横找或竖找（从比例式的分子线段或分母线段中找相应的三角形）.

2.相似若是不好找，等量代换试一试

若在化成比例式后，不能通过直接找两个三角形相似来实现等积的证明，此时可通过查找问题中所隐含的相等的线段或相等比值的条件，用等线段或相等的比值来代替比例式中的相关量，再在此基础上通过找三角形相似来证明等积问题.

例2 如图2，▱ABCD中，E为边AD延长线上的一点，BE交CD于F.试证明：CD·BC=AE·FC.

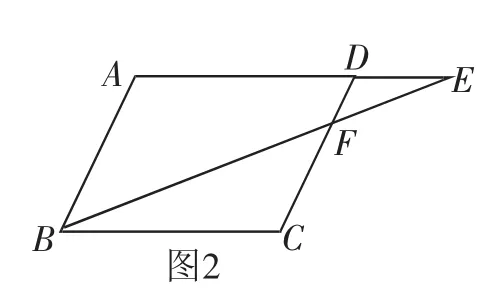
证明：因为四边形ABCD是平行四边形，

所以∠A=∠C，AB=CD，AD∥BC.

所以∠CBF=∠AEB.

又因为AB=CD（已证），

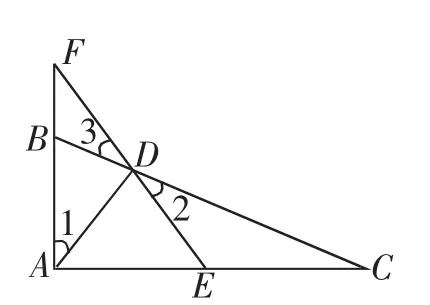
图3

例3 如图3，已知在△ABC中，∠BAC=90°，AD⊥BC，E是AC的中点，ED交AB的延长线于点F.求证：AB·AF=AC·DF.

证明：（略）.

评注：在证明比例式时，如果直接证明或等量代换有困难时，则可以考虑等比代换或等积代换，利用中间比（积）过渡.

3.平行线段转比例，两端各自拉关系

证明等积时，在无法证明两个三角形相似且又无法找到问题中所蕴含的等线或相等的比值时，可进行观察，看看问题中是否含有平行的条件，可借助平行线成比例的有关性质来查找问题所含的相等的比值.

图4

例4 如图4，梯形ABCD中，AB∥DC，E是AB的中点，直线DE分别与对角线AC，直线BC相交于M和N求证：MD·NE=ME·ND.

由图中无法直接找到相关的三角形相似，也没有相等的线段.

这时需要考虑用第三个比例式来过渡搭桥.紧扣条件中的AB∥DC，由平行线分线段成比例定理发现两式中唯一不同之处仅在于AE、BE，而已知条件中明确了E是AB的中点，即AE与BE是相等的，从而再借助这一等价关系可得进而证明

评注：“等积式化比例式，横找竖找找相似；相似若是不好找，等量代换试一试；平行线段转比例，两端各自拉关系”的解题思路，仅仅是等积问题众多证明思路中的一种.等积问题千变万化，不同的等积问题仍需要进行具体的分析，选择恰当的方法.相信只要在等积问题的证明过程中不断摸索，不断总结，就能找到一种比较适用的证明方法和证明技巧.