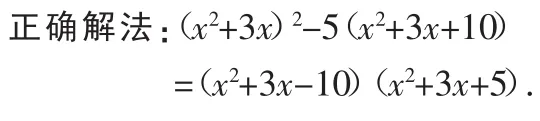因式分解常见解题误区

☉河南大学附属中学 桑静华

因式分解是初中学习的重要内容，也是每年中考的必考内容，同时是同学们学习中的一个难点.同学们在遇到因式分解问题时，总会出现这样或那样的错误.现把常出现的错误归纳如下，望引起同学们的注意.

一、符号处理不当导致错误

1.符号未改变.

例1 因式分解：2x－2y＋y2－x2.

分析：提公因式后，剩余的因式为多项式，但括号前为负号时，括号内应改变符号，此题的解法中忽略了这一点.

2.符号未作处理.

例2 因式分解：（1）－a2＋b2；（2）－a2－2ab－b2.

分析：上面的两题都没有构造公式，而是直接运用公式分解，但因符号处理不当而导致错误.

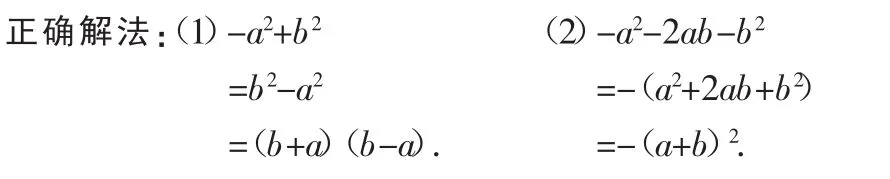
二、分解不彻底导致错误

1.错用公因式.

例3 因式分解：4xy2－6x2y.

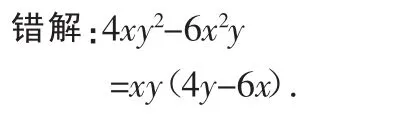
分析：此题在找公因式时，忽略了数字系数，错把公因式当成xy，正确的公因式为2xy.

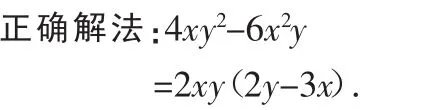
2.用公式不彻底.

例4 因式分解：（1）a3b－2a2b＋ab；（2）x4－1.

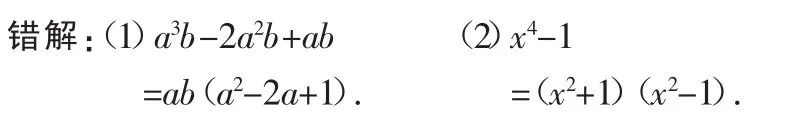
分析：上面分解因式的结果还能再分解，但由于对公式的运用不熟而导致分解不彻底.

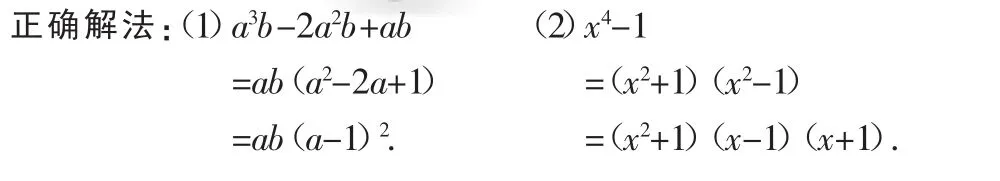
三、不能正确运用公式导致错误

1.理解公式错误.

例5 因式分解：4x2－y2.

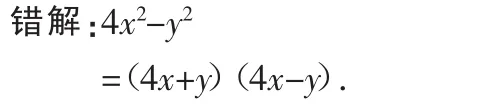
分析：没有完全理解平方差的公式，公式中的a对应于题中的2x，并不是4x.

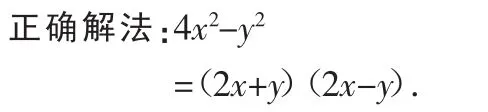
2.公式的特点不明确.

例6 因式分解：x2－5x－6.

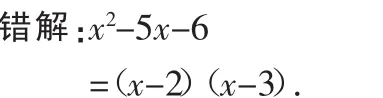
分析：对公式的系数特点分析不透彻，只注意了一次项系数，而忽略了常数项，虽然（－2）＋（－3）＝－5，但（－2）×（－3）≠－6.

3.运用公式不当.

例7 因式分解：（1）x2＋2x＋4；（2）x2－4y.

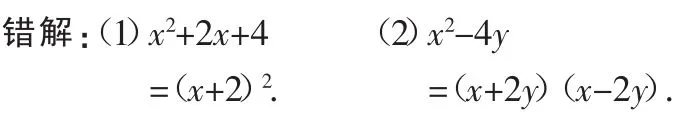
分析：错误的原因是没有仔细观察多项式的形式，没有认真判断是否符合公式的特点，凭感觉分解因式.实际上，题目所给的两个式子都不可分解.

四、没有整体观念导致错误

例8 因式分解：（x2＋3x）2－5（x2＋3x+10）.

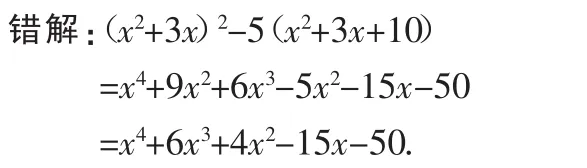
分析：没仔细观察多项式的特点，急于展开合并同类项，把简单的问题复杂化，导致无法进行因式分解，应把x2＋3x看做整体，利用公式来分解因式.