浅析解直角三角形的应用问题

☉山东省莒南县筵宾镇初级中学 徐淑杭

浅析解直角三角形的应用问题

☉山东省莒南县筵宾镇初级中学 徐淑杭

解直角三角形的应用是初中数学的一个很重要的知识点，在历次中考中所占的分值基本都在10分以上，主要考查在物高测量、建筑设计、坡角、坡比、堪测矿藏、图案设计、气象预报、工程技术、物理学、医学、航海航空等诸多领域应用，这些知识需要学生根据已知条件解直角三角形的方法，运用解直角三角形的知识解决问题.具体做到：1了解某些实际问题中的仰角、俯角、坡度等概念；2将实际问题转化为数学问题，建立数学模型；3涉及解斜三角形的问题时，通过作适当的辅助线构造直角三角形，使之转化为解直角三角形的计算问题而达到解决实际问题的目的.关于解直角三角形应用有如下知识点和考点.

一、知识点与技能扫描

1.课程内容解读

（1）通过实例（梯子的倾斜程度）认识锐角三角函数的含义.

（2）知道3 0°、45°、60°角的三角函数值.

（3）会使用计算器由锐角求它的三角函数值，由已知三角函数值求锐角.

（4）熟悉利用解直角三角形对物高进行测量的方法.

（5）掌握运用三角函数解决与直角三角形有关的实际问题.

2.中考考题的共同点

（1）均考查了运用三角函数解决与直角三角形边角有关的实际问题.

（2）都要借助辅助线完成.

（3）都能分解为含3 0°、45°、60°的特殊直角三角形.

（4）结果都有限制条件.

二、中考典例剖析

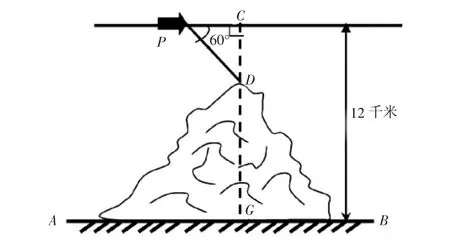
图1

例1 如图1，一架飞机在空中P处探测到某高山山顶D处的俯角为60°，此后飞机以3 00米/秒的速度沿平行于地面AB的方向匀速飞行，飞行10秒到山顶D的正上方C处，此时测得飞机距地平面的垂直高度为12千米，求这座山的高（精确到0.1千米）.

答案提示：延长CD交AB于G，则CG=12千米.

依题意得PC=3 00×10=3 000米=3千米.

在Rt△PCD中，

答：这座山的高约为6.8千米.

考点剖析：本题是一道较简单的实际应用题，只需要作出辅助线构造直角三角形，然后在直角三角形中利用锐角三角函数的知识，就可以轻松解决问题.

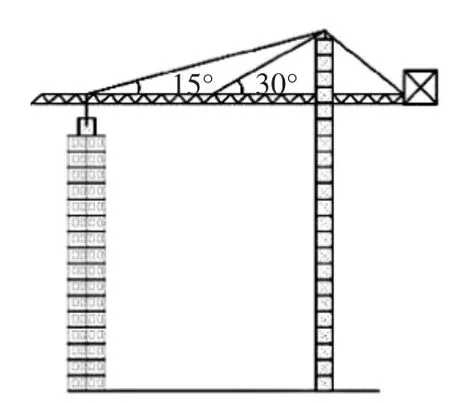
图2

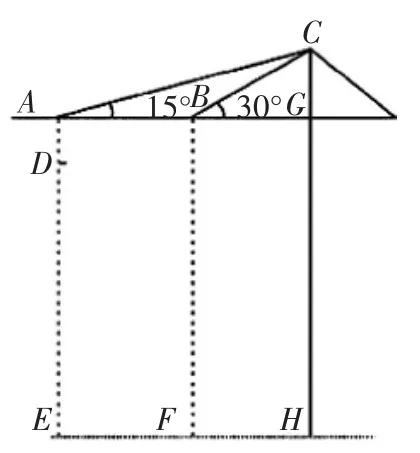
图3

例2 图2为已建设封顶的16层楼房和其塔吊图，图3为其示意图，吊臂AB与地面EH平行，测得A点到楼顶D点的距离为5m，每层楼高3.5m，AE、BF、CH都垂直于地面，EF=16m，求塔吊的高CH的长.

答案提示：根据题意得：DE=3.5×16=56，AB=EF=16.

答：塔吊的高CH的长为69m.

考点剖析：本题是一道关于生活中塔吊的题目，乍看图形比较复杂，但是静心看一下图形解决起来是比较简单的.主要考查了将实际问题转化为数学问题的能力，只要正确地运用锐角三角函数的知识就可以得到正确答案.

例3 在一个阳光明媚、清风徐来的周末，小明和小强一起到郊外放风筝﹒他们把风筝放飞后，将两个风筝的引线一端都固定在地面上的C处（如图4）.现已知风筝A的引线（线段AC）长20m，风筝B的引线（线段BC）长24m，在C处测得风筝A的仰角为60°，风筝B的仰角为45°.

（1）试通过计算，比较风筝A与风筝B谁离地面更高.

（2）求风筝A与风筝B的水平距离.

图4

（精确到0.01m；参考数据：sin45°≈0.707，cos45°≈0.707，tan45°=1，sin60°≈0.866，cos60°=0.5，tan60°≈1.732）

答案提示：（1）分别过A，B作地面的垂线，垂足分别为D，E.

即风筝A与风筝B的水平距离约为6.97（m）.

考点剖析：本题是同学们比较感兴趣的放风筝问题，主要是应用直角三角形的边角关系来解决本题，首先构造直角三角形，分别过A，B作地面的垂线，垂足分别为D，E.第（1）问是已知角和斜边，利用正弦求角的对边，求出两个对边就可以比较；第（2）问已知角和斜边，利用余弦求角的邻边.

三、复习方法建议

（1）精——将考点、考向、方法、技巧、题例等呈现给学生，所呈现要精而又精.

（2）准——做到不偏离航线，使复习与中考接近起来，提高命中率，也使学生感受提前进入中考，这就做到了“准心复习”.

（3）全——作为中考前的复习，一定要做到全面系统，不遗漏任何一个复习点不给学生造成遗憾，这要求我们对初中知识点做出全面的串接.

（4）实——在复习中不能只享受教师整理得如何，更要将复习过程和结果实实在在地落实到每一位学生身上.

解直角三角形应用的学习要全面落实“三基”，教师重视提炼教学思想，发展理性思维.注意学生阅读理解能力和书面表述能力的培养，关注学生观察问题、分析问题、处理问题的方法与能力，应加强运算的合理性和科学性的教学，解直角三角形的应用所涉及的知识点主要是“勾股定理”和“锐角三角函数”，扎实、牢固地掌握好这两部分内容是正确解直角三角形的基本前提，只要掌握好这两部分内容，就等于掌握了解直角三角形的有力工具，只要能够灵活运用，就能游刃有余地解决问题.