因式分解切记四个“必须”

☉江苏省泰兴市黄桥初级中学 段圣凤

把一个多项式写成几个整式的积的形式叫做因式分解.因式分解的基本思路：首先考虑是否有公因式可以提取，其次考虑能否运用公式进行分解，最后要检查每一个因式是否已经完全分解.下面对因式分解的结果与同学们谈几个基本要求：

一、必须是恒等变形的结果

分析：有些同学误用等式的性质，把多项式各项都乘以4，得到a3b2+4ab3c，再分解成ab2（a2+4bc）.显然，该解法没有遵循恒等变形这一原则，所得结果是错误的.

正确解法：

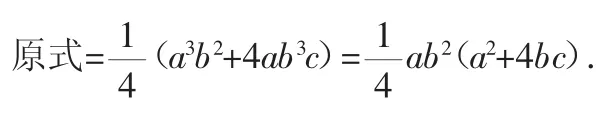
二、必须是若干因式的乘积

例2 分解因式：6mx－6mx2－24m3.

分析：有些同学注意到前两项可运用提取公因式法，于是将其分解因式结果为6mx（1－x）－24m3，这个结果虽然是恒等变形，但不是几个因式的乘积形式，所得结果是错误的.

正确解法：

原式=6m（x－x2－4m2）.

三、结果形式必须是最简化的

结果中的每个多项式因式不能有同类项，相同因式应写成幂的形式.

例3 分解因式：（1）（a－b）2+2a（a－b）；（2）（x2+3x）2－（x+3）2.

分析：有些同学分解结果不符合要求：（1）（a－b）［（a－b）+2a］；

（2） （x+3）（x+1）（x+3）（x－1），结果不是最简形式，应进一步化简.

正确解法：

（1）原式=（a－b）（3a－b）.

（2）原式=（x+3）2（x+1）（x－1）.

四、必须分解到不能再分解为止

例4 分解因式：3mx－6my.

分析：有些同学直接提取公因式字母m，忽视了常数，所得错解为m（3x－6y）.

正确解法：

原式=3m（x－6y）.

例5分解因式：（x+y）2－（xy+1）2.

分析： 有同学分解为（x+y+xy+1）（x+y－xy－1），这个结果是不正确的，因为最后的结果还可以继续分解.

正确解法：

原式=（x+y+xy+1）（x+y－xy－1）=（x+1）（y+1）（x－1）（1－y）.

例6 分解因式：a4－8a2b2+16b4.

分析： 有些同学直接运用公式法得到（a2－4b2）2，这个结果是错误的，因为在有理数范围内，还可以将（a2－4b2）继续分解.

正确解法：

原式=（a2－4b2）2=（a+2b）2（a－2b）2.

点评：因式分解的结果必须是几个因式的乘积，且每个因式必须都是不能再分解为止，特别是观察积中有二次或二次以上的因式时，看看能不能再分解.