数形结合思想在中学数学的应用
☉湖北省武汉市旭光学校 张东林
一、数形结合思想的概述
数与形是数学中两个最古老、最基本的元素,是数学大夏深处的两块基石.在解决数学问题时,常常根据数学问题的条件和结论之间的内在联系,将数的问题利用形来观察,揭示其几何意义;而形的问题也常借助数去思考,分析其代数含义,如此将数量关系和空间形式巧妙地结合起来,并充分利用这种“结合”,寻找解题思路,使问题得到解决的方法称之为数形结合的思想方法.
数形结合是一个数学思想方法,包含“以形助数”和“以数辅形”两个方面,其实质是将抽象的数学语言与直观的图像结合起来,关键是代数问题域图形之间的相互转化,它可以使代数问题几何化,几何问题代数化.下面结合具体实例谈谈数形结合思想在解题中的应用.
二、以形助数
几何图形具有直观易懂的特点,所以在谈到“数形结合”时,更多的老师和学生更偏好于“以形助数”,利用几何图形解决代数问题,常常会产生“出奇制胜”的效果,使人愉悦.几何直观运用于代数主要有以下几个方面:
(1)利用几何图形帮助记忆代数公式,例如:
a)正方形的分割图可以用来记忆完全平方公式;
b)将两个全等的梯形拼成一个平行四边形可以用来记忆梯形面积公式等.
(2)利用数轴或坐标系将一些代数表达式赋予几何意义,通过构造几何图形,依靠直观帮助解决代数问题,或者简化代数运算.比如:
a)绝对值的几何意义就是数轴上两点之间的距离;
b)数的大小关系就是数轴上点的左右关系,可以用数轴上的线段表示实数的取值范围;
c)互为相反数在数轴上关于原点对称(更一般地:实数a与b在数轴上关于对称,换句话说,数轴上实数a关于b的对称点为2b-a).
(3)利用函数图像的特点把握函数的性质:一次函数的斜率(倾斜程度)、截距,二次函数的对称轴、开口、判别式、两根之间的距离等.
(4)一元二次方程的根的几何意义是二次函数图像与x轴的交点.
(5)函数解析式中常数项的几何意义是函数图像与y轴的交点(函数在x=0时有意义).
(6)锐角三角函数的意义就是直角三角形中的线段比例.

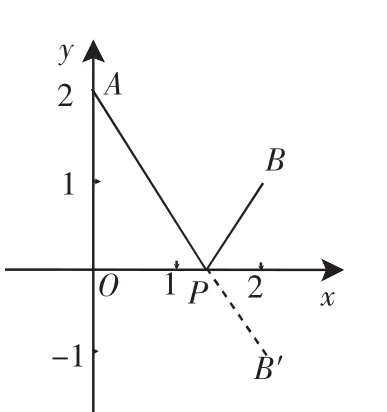
图1
即看做是坐标系中一动点(x,0)到两点(0,2)和(2,1)的距离之和,于是本问题转化为求最短距离问题.
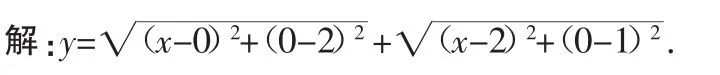
令P(x,0)、A(0,2)和B(2,1),则y=PA+PB.
作B点关于x轴的对称点B′(2,-1),则y的最小值为AB′=
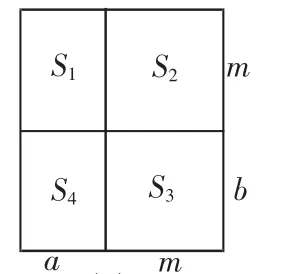
图2
分析:本例证法虽有很多,但若用几何图形面积去证,则更能看清问题的实质.
证明:利用a,b,m构造矩形(如图2).S1=ma,S3=mb,因为a 所以S1+S4 例3 已知:0 图3 证明:如图3,作边长为1的正方形ABCD,在AB上取点E,使AE=a;在AD上取点G,使AG=b,过E,G分别作EF∥AD交CD于F;作GH∥AB交BC于H.设EF与GH交于点O,连 接 AO,BO,CO,DO,AC,BD.由题设及作图知△AOG、△BOE、△COF、△DOG均为直角三角形,因此 小结:在求证条件不等式时,可根据题设条件作出对应的图形,然后运用图形的几何性质或者平面几何的定理、公理去建立不等式使结论获证. 分析:根据正切函数的意义不难构造出满足条件的角α、β(如图4),怎样构造这两个角的和是解决这个问题的关键.将图4中下面的图翻转到上图的下面,就形成了如图5的图形,角α+β也就构成了. 证明:如图5,连接BC,易证:△ABD≌△CBE,从而△ABC是等腰直角三角形,于是:α+β=45°. 图4 图5 要在解题中有效地实现“数形结合”,最好能够明确“数”与“形”常见的结合点,从“以数助形”角度来看,主要有以下两个结合点. (1)利用数轴、坐标系把几何问题代数化(在高中我们还将学到用“向量”把几何问题代数化). (2)利用面积、距离、角度等几何量来解决几何问题,例如:利用勾股定理证明直角、利用三角函数研究角的大小、利用线段比例证明相似等. 例5 如图6,过正方形ABCD的顶点C任作一直线与AB、AD的延长线分别交于E、F.求证:AE+AF≥4AB. 分析:这是“形”的问题,但要直接从“形”入手很棘手.引导学生将结论变为 图6 从此式形式上看,联想起一元二次方程根的判别式,从而把“形”的问题转化成“数”的问题来解决. 证明:设AB=a,AE=m,AF=n.连接AC,则 所以mn=a(m+n).设m+n=p,mn=ap.所以m,n是方程x2-px+ap=0的两根,而m,n为实数,故△=p2-4ap≥0,又p>0,所以p≥4a,即AE+AF≥4AB. 例6 如图7,在正△ABC的三边AB,BC,CA上分别有点D,E,F.若DE⊥BC,EF⊥AC,FD⊥AB同时成立,求点D在AB上的位置. 分析:先假设符合条件的点D,E,F已经作出,再利用已知条件,寻找线段与角之间的数量关系,列出含有待求量的等式(方程),以求其解. 解:设AB=1,AD=x. 因为△ABC为正三角形,且DE⊥BC,EF⊥AC,FD⊥AB, 故 AF=2x,CF=1-2x,CD=2CF=2-4x,BE=1-CE=4x-1,BD=2BE=8x-2. 而AD+BD=1,即x+(8x-2)=1. 小结:几何中存在着这样一类问题,即几何图形中的某些点的位置或线段的长度或角度的大小不能依题意画出来,只有根据已知条件求出某一些量时,图形才能画出.而求那些量的方法,常常是通过列方程(组),即转化为代数方程求解. 总之,数形结合思想是数学中基本而又重要的思想,是解决数学试题的一种常用方法与技巧,特别是在解决选择、填空题中发挥着奇特功效.数学家华罗庚曾指出:“数缺形时少直观,形少数时难入微;数形结合百般好,隔裂分家万事非.”可见数形结合的思想可以使某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维,有助于把握数学问题中的本质.在中考复习时,同学们必须随时注意运用数形结合思想,复习中要以熟练技能、方法为目标,加强这方面的训练,以提高解题能力和速度. 1.程旷主.巧学初中数学80法.农村读物出版社 2.九年义务教育初中数学课本.北京:人民教育出版社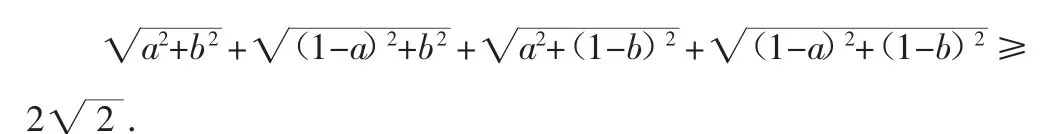
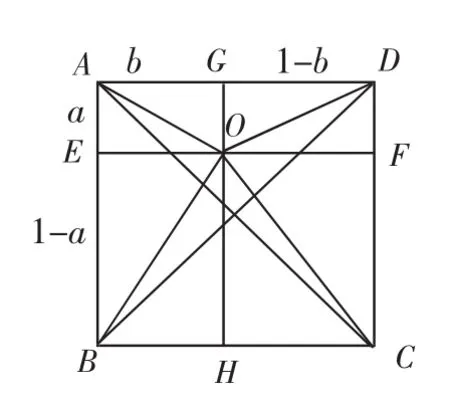

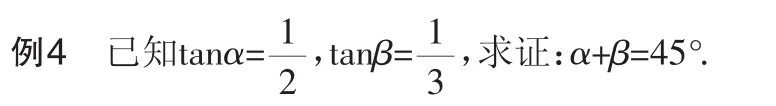
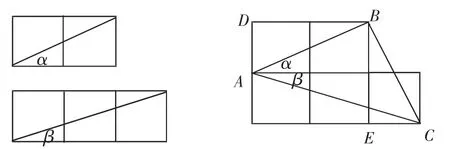
三、以数解形