对初中数学“求值问题”的解题方法探究

☉湖北省郧西县夹河镇金銮山中学 王家平

一、用主元法求值

例1 已知a+b+c=0，a2+b2+c2=4，求：a4+b4+c4的值.解：（视a，b为主元）

由已知得，a+b=-c，a2+b2=4-c2.

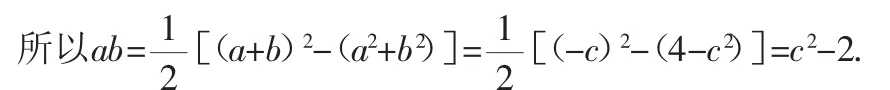
所以a4+b4=（a2+b2）2－2a2b2=（4-c2）2-2(c2-2)2=8-c4.

所以a4+b4+c4=8.

二、用设参数法求值

例2 设m，n，p均为正实数，且m2+n2-p2=0，求 p m+n的最小值.

解法2：利用4mn≤（m+n）2这个结论，仿“解法1”的手法也可处理.

三、用构造法求值

解法1：由绝对值的几何意义知，本题就是要在数轴上求一点M（x），使它到点A（－6）的距离的2倍与到点B（5）的距离之和最小.

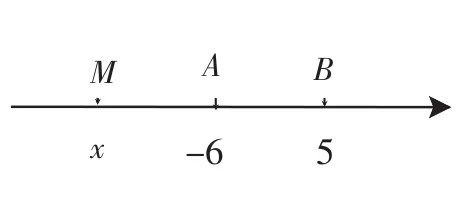
⑵当x=-6时，y=MB=AB=11；

⑶当-6AB=11；

⑷ 当 x=5时 ，y=2MA=2AB=22；

⑸当x>5时，y=2MA+MB>2AB=22.

解法2：用“找零点分段讨论法”也可处理.

四、用倒数法求值

五、用倒数式求值

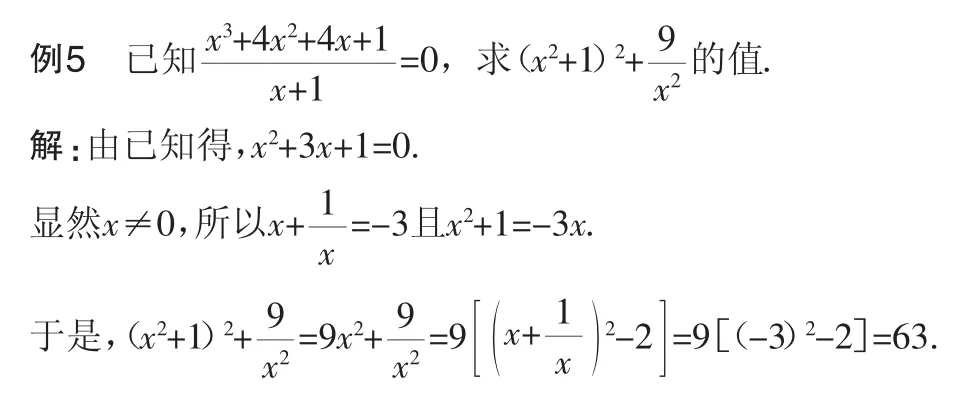
六、用整体代入法求值

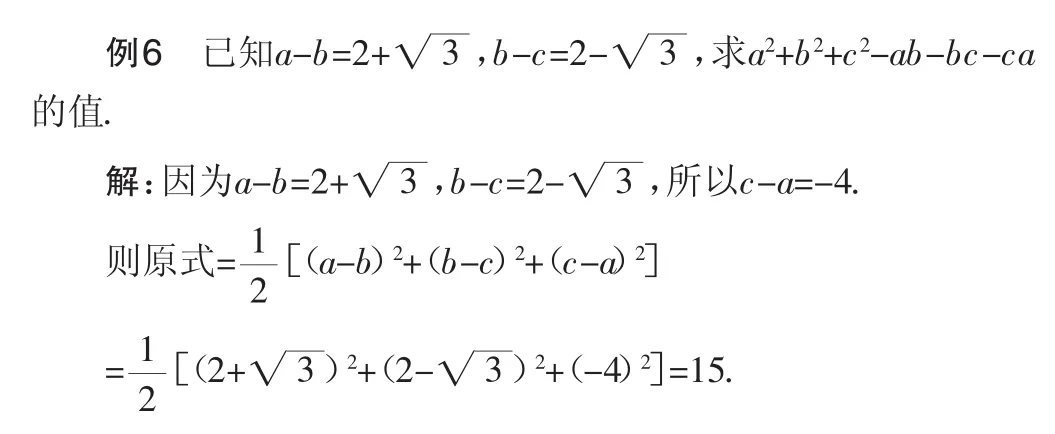
七、用升幂法求值

八、用放缩法求值

而n为正整数，

所以解不等式组得：1

于是取n=2，它恰能满足原方程.

九、用非负数的性质求值

所以（2008a+5.12b）14.28c=［2008×（±2）+5.12（-3）］14.28×0=1.

总之，初中数学“求值问题”的解题方法很多，我们在平常的练习中，一定要善于归纳小结！