三角板穿插引出的一则面积最值问题

☉浙江省台州市黄岩区沙埠中学 赵晓华

☉浙江省台州市黄岩区高桥中学 蔡历亮

三角板穿插引出的一则面积最值问题

☉浙江省台州市黄岩区沙埠中学 赵晓华

☉浙江省台州市黄岩区高桥中学 蔡历亮

三角板是中学生学习数学时不可或缺的工具，通过操作三角板，可以发现许多有趣的、有意义的数学问题.如：多付三角板拼多边形，用三角板进行平移、翻折、旋转变换.而比较新颖的是利用三角板进行穿插，三角板中间都挖有圆孔或三角孔，如果用其中一块三角板去穿插另一块三角板，那会形成怎么有趣的数学问题呢？

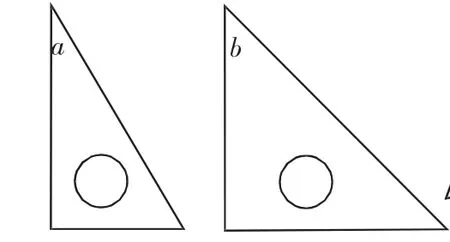
图1

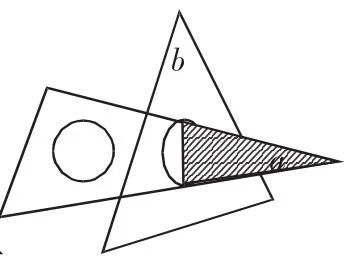
图2

今有一副三角板（如图1），中间各有一个直径为2cm的圆洞，现用三角板a的30°角的那一头插入三角板b的圆洞内（如图2），求三角板a通过三角板b的圆洞的那一部分的最大面积（不计三角板的厚度）.

这是由三角板穿插引出的面积最值问题，本题难度较大，分析难度成因，主要有两点：

（1）“三角形a的30°角的那一头插入三角板b的圆洞内”需要较强的空间想象能力，问题抽象，学生不易理解，难以确定何时面积最大.

（2）即便知道穿插成何种位置时面积最大，计算相应面积也很困难.

笔者与学生进行交流、研究，发现本题的解答方法较多，现归纳3种解法供读者参考.

先将本问题转化为“解三角形”.已知：如图3，△ABC中，BC=2，∠A=30°，求△ABC面积的最大值.

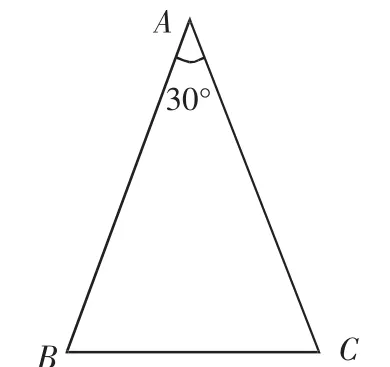
解法一：

（1）当△ABC面积最大时，△ABC的形状不可能为钝角三角形.否则，不妨设∠ACB＞90°（如图4）.过B作BD⊥AC于D，延长CD到C1，使C1D=CD，则△ABC1中，BC1=2，∠A=30°，S△ABC1＞S△ABC，与△ABC面积最大矛盾.

图4

图5

（2）当△ABC面积最大时，△ABC是∠A为顶角的等腰三角形.

证明：如图5，设△ABC面积最大时，AB=xcm、AC=ycm，过B作BD⊥AC于D.在Rt△ABD中，∠ADB=90°，∠A=30°.

当x=y时，S△ABC的面积最大，此时△ABC是等腰三角形，且∠A为顶角.

（3）当△ABC是∠A为顶角的等腰三角形时，

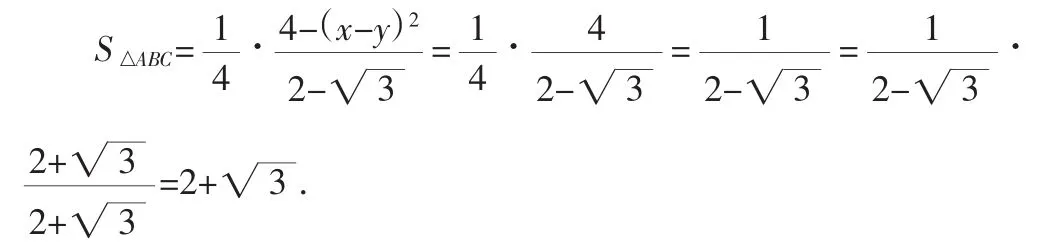
答：当△ABC是等腰三角形时，△ABC的面积最大，即三角板a通过三角板b的圆洞的那一部分的最大面积为（2+）cm2.

解法二：

图6

图7

（1）△ABC中，让BC=2cm位置固定不动，变换∠A的位置，保证∠A=30°不变，即点A在以BC为弦，所含圆周角等于30°的两段弧（不含端点B、C）上运动（如图6）.易知，当A是在圆弧中点时，△ABC的面积最大，此时△ABC是等腰三角形，∠A是顶角.

（2）当△ABC是∠A为顶角的等腰三角形时，过B作BD⊥AC于D（如图7），设AB=2xcm.在Rt△ABD中，∠ADB=90°，∠A=30°.

图8

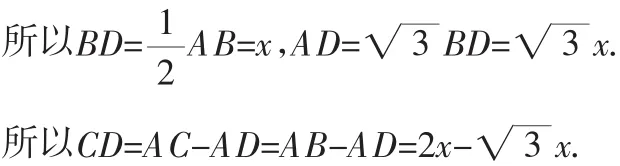
答：当△ABC是等腰三角形时，△ABC的面积最大，即三角板a通过三角板b的圆洞的那一部分的最大面积为（2+）cm2.

解法三：

（1）由解法2第（1）问知：当△ABC是顶角为∠A的等腰三角形时，△ABC的面积最大.

（2）当△ABC是顶角为∠A的等腰三角形时，过A作AD⊥BC于D（如图8）.

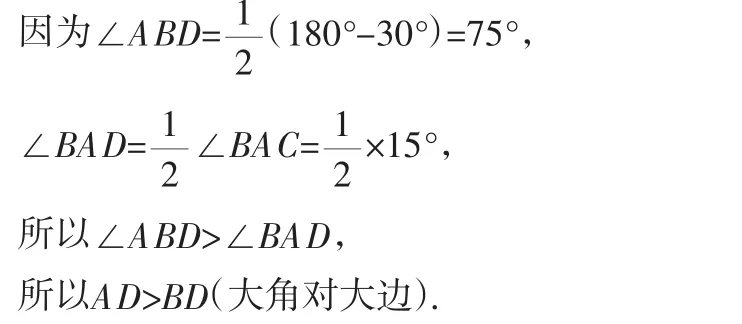
当D沿DA方向运动时（运动到点A时停止），BD会不断变大，AD会不断变小，则在线段AD上存在一点E，使D运动到E时，BD=AD，即在线段AD上存在一点E，使BE=AE.

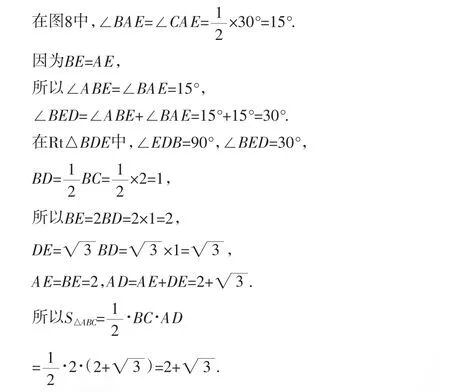
答：当△ABC是等腰三角形时，△ABC的面积最大，即三角板a通过三角板b的圆洞的那一部分的最大面积为（2+）cm2.

解法二的第（1）部分的证明方法，对于∠A的度数并没有限制，因此可对本题结论进行推广得到如下结论：如果已知一个三角形的一角θ及该角的对边，那么当该三角形是顶角为θ的等腰三角形时面积最大.