关于等腰三角形解题的探讨

安艳菊

等腰三角形的有关知识点，一直备受中考命题者的青睐，在历年各省中考试题中频繁出现.特别是等腰三角形的有些题目经常需要分类讨论才能作出解答，这使得等腰三角形在同学们面前又多了一层神秘的面纱.其实，解此类问题还是有规律可循的.下面是笔者归纳的几种有关等腰三角形的分类讨论题，希望对学生的学习有所帮助.

笔者以为解等腰三角形类题型一般要考虑以下几种情形.

一､考虑哪一条边是底边，哪一条边为腰

例1已知等腰三角形的两条边长分别为4和6，那么它的周长为( ).

A.14B.18C.18 D.14或16

解:当腰长为4，底边为6时，周长为14.

当腰长为6，底边为4时，周长为16.

且都满足三角形两边之和大于第三边的关系.

所以答案为D.

例2在平面直角坐标系xOy中，已知A(2-2)，在y轴上确定点P，使△AOP为等腰三角形，则符合条件的点P 共有().

A.2个 B.3个 C.4个 D.5个

答案:C

分析:注意:若△AOP为等腰三角形，则已知边OA为既可为腰亦可为底边.

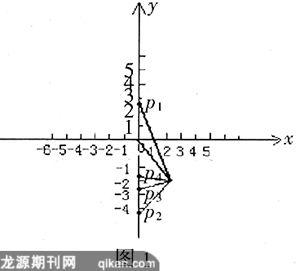
分情况讨论，如图1，当OA为等腰三角形的腰时，有△OP1A(OA=OP1)，△OP3A(OA=OP3)，△AOP2(OA=AP2);当OA为等腰三角形的底时，有△P4OA(P4O= P4A).

二､考虑哪一个角是顶角，哪一个角为底角

例3(1)有一个角是80°的等腰三角形的另外两个角分别是____.

(2)如果等腰三角形有一个外角等于140°，那么它的顶角度数是____.

解析:(1)当80°为顶角时，另外两个角为底角，度数分别为50°，50°;

当80°为底角时，另外两个角为一个顶角一个底角时，度数分别为20°､80°.

(2)当140°为顶角的外角时，顶角为40°;

当140°为底角的外角时，顶角为100°.

三､因等腰三角形的高的特殊性，需考虑等腰三角形类型(锐角､直角还是钝角三角形)

例4等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为().

A.60°B.120° C.60°或150°D.60°或120°

分析:当为锐角等腰三角形时，如图2，顶角为60°.

直角三角形不符合题意.

钝角三角形时，如图3，顶角为120°.

答案:D.

类题:已知△ABC中，AB=AC，CD是AB边上的高，且△ACD恰为等腰三角形，则∠BCD=____.

答案:22.5°或67.5°.

例5已知BD 是△ABC一腰上的高，且∠ABD=50°，求△ABC的几个内角的度数.

分析:因为涉及到等腰三角形的高，而等腰三角形的高有其特殊性，所以要充分考虑所涉及的等腰三角形的类型.

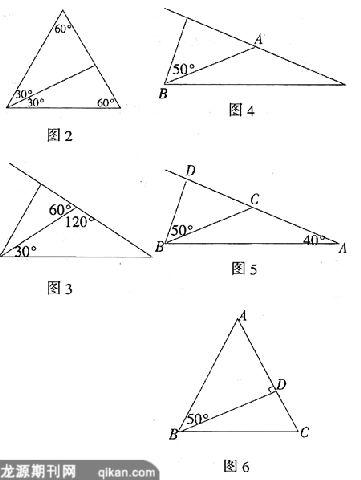
解:(1)当△ABC为钝角三角形时，∠A既可以作顶角也可以作底角.

①当∠A作顶角时，如图4，△ABC的三个内角分别为140°，20°，20°.

②当∠A作底角时，如图5，△ABC的三个内角分别为100°，40°，40°.

(2)当△ABC是锐角三角形时，∠A只可能做顶角，如图6，△ABC的三个内角分别为40°，70°，70°.

(3)△ABC不可能是直角三角形.

因此△ABC的三个内角度数分别为140°，20°，20°或100°，40°，40°或40°，70°，70°.

由以上归纳我们可以看到:(1)首先要认清等腰三角形，在求解涉及等腰三角形的题目中，若没有明确哪一条是底或腰，哪一个为顶角或底角时，要分情况讨论，才能使所得的答案完整.(2)其次要明确等腰三角形的特殊性，凡是联系到需要做等腰三角形的高的题目时，则要分别考虑三角形是锐角，直角或钝角三角形，确定高的位置后求解.只要你看清了等腰三角形的真面目，以后解题也就不怕了.