正弦定理惹的祸?

☉湖南科技学院数学与计算科学系 周宇剑

一、问题的引出

刚学完正弦定理，小明先后做了以下几道题：

小明第（1）题填了60°，同桌说他错了.小明想了想，发现自己丢掉了和60°正弦值相等的120°角.

小明接着做第（2）题时，很得意地填了30°或150°.但同桌又说他错了.小明疑惑了，这次考虑到和30°正弦值相等的150°角，怎么又错了呀？仔细一想，发现150°不符合题目要求.

小明更仔细地计算完第（3）题，说“这下总该对了吧？”，与同桌一对照，两人的答案不同，仔细对比了一下，求c边的结果一样，之后的解法不一样，他俩的具体解法如下.

故B=75°或105°.

当B=75°时，A=180°-B-C=75°.

当B=105°时，A=180°-B-C=45°.

仔细看完解题过程和步骤后，小明和同桌都茫然了，真看不出来到底谁的解法有问题？小明拍拍脑袋说：“哎，都是正弦定理惹的祸！到底怎么做才能对啊？”

二、问题探究及解决策略

对刚学完正弦定理的学生来说，很容易出现上述错误.这几道题目涉及到已知两边和一角解三角形的问题.这类问题又分为两种类型：已知两边及一边的对角和已知两边及它们的夹角.现就这两种类型的问题分析如下：

1.已知两边及一边的对角.

在△ABC中，已知BC=a，AC=b，A（0°＜A＜180°），求B.

该问题需分三种情况讨论.

（1）当a>b时（已知角的对边大于所求角的对边）.

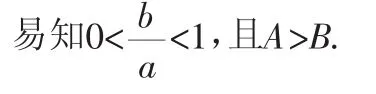
（2）当a=b时（两已知边相等）.

若90°≤A＜180°，由B=A，知原题无解；若0°＜A＜90°，由B=A，知原题有一解.（3）当a＜b时（已知角的对边小于所求角的对边）.

教学过程中要提醒学生在实际解题中要注意判别已知条件中的两边之间的关系，依情况和是否具有实际意义而解.

2.已知两边及它们的夹角.

在△ABC中，已知BC=a，AC=b，C（设a＜b，0°＜C＜180°），求A和B.

这种类型的题目如果按照上种类型用正弦定理来求角，均要考虑A或B是否为钝角，如果为钝角时又要验证是否有实际意义，则解题既加大了计算量，又耽误时间.教学中要帮助学生理解判断三角形全等的方法中就有边角边（SAS）判定定理，因此，已知两边及它们的夹角时，能够唯一确定三角形.故此类型必定有唯一解.此类问题的解题思路：

方法1：用余弦定理求A或B（唯一确定解），再用三角形内角和定理求出另一角.这种计算免去了对所求角是锐角还是钝角的思考，但计算量稍微大一点.

方法2：用正弦定理求A或B，再用三角形内角和定理求出另一角.这种方法计算量相对简单些，但一些初学的同学理不清头绪，现剖析如下.

（1）当90°≤C＜180°时.

此时，A、B均为锐角，可用正弦定理任意求A或B的值，原题有一解.

（2）当0°＜∠C＜90°时.

求出c后，比较a、b、c的值.

若c值最小，即c＜a＜b，则用正弦定理求出a、b中较小边a所对的角A，因为a＜b，所以A不能为直角或钝角，原题有一解.

若c值处于中间位置，即a＜c＜b，则A＜C＜B.先用正弦定理求最小边a所对的A，由于A最小，故A不能为直角或钝角，原题有一解.

若c最大，即a＜b＜c，则A＜B＜C.A、B均为锐角，原题有一解.

前面小明与同桌做的第3题表面上解得很好，但都存在问题.在已知条件中包含一个隐含条件：a＜b，所以，在△ABC中，A＜B.因此，小明的解法中A=135°、B=15°这个结果要舍去；小明同桌的解法中A=75°、B=75°这个结果要舍去.

已知三角形的两边及它们的夹角，求其余两角的问题解题策略：求出第三边c的值后，比较三条边a、b、c的大小，可用正弦定理求出已知边a与b中较小的边所对的角，这个角就不可能是钝角或直角，可直接确定该角的值.这样就避免了用正弦定理时讨论各角是锐角还是钝角的烦恼.