吃透考纲精神,把握命题规律

☉湖北省武汉市黄陂区第一中学 卢 琼（特级教师）

《2012年普通高等学校招生全国统一考试湖北卷考试说明》数学科部分（以下简称《考纲》）终于与大家见面了，今年我省数学《考纲》的各项要求明确具体.解读《考纲》，关注其蕴含的信息，新课程高考第一年，平稳过渡，无缝对接，湖北省今年高考数学命题风格较往年变化不会太大；学习《考纲》，重点分析考试性质、命题指导思想、考核目标与要求、考试范围与要求层次；研究《考纲》，明确它在强化什么、淡化什么、回避什么，加深课程改革和高考改革一致性的认识，树立高三复习教学新理念.

笔者在文中将结合教学实例，以题源的呈现、题源的解析、题源的探究、题源的变式与拓展为主线，浅谈如何立足于课本，吃透考纲精神，把握命题规律这一主题.

一、领会《考纲》的命题思想，在回归梳理中寻找题源

《考纲》的命题指导思想是：命题遵循《普通高中数学课程标准（实验）》和《2012年普通高等学校招生全国统一考试大纲（课程标准实验版）》，试题在源于教材的同时又具有一定的创新性、探究性和开放性，既考查考生的共同基础，又考查考生的学习潜能，以满足选拔不同层次考生的需求.

课本是高考试题的重要来源，很多高考试题都是由课本例题和习题改进、改型、综合、引申、演变而来，翻开近几年湖北高考试卷，无论文理科均有100分左右的题目源于教材，兑现了《考纲》的承诺.因此，我们在复习教学中，引导学生回归课本，梳理教材，在课本的例题和习题中寻根探源，让学生跳出题海，不做题奴，走高效备考之路.

题源呈现设f（α）=sinxα+cosxα，x∈{n|n=2k，k∈N*}，利用三角变换，估计f（α）在x=2、4、6时的取值情况，进而对x取一般值时f（α）的取值范围作出一个猜想.

这是人教版数学教材《必修4》习题3.2B组中的第5题（第157页），主要考查三角函数的基本知识、三角恒等变形的基本技能和代数推理的基本方法，此题看似平凡，但设问方式不落俗套，既具开放性又具探究性，给人以无限想象的空间，留下进一步研究的接口，必然深受高考命题人青睐.如果我们在教学中，也能充分利用这些素材，开发这些资源，帮助学生理解掌握常规思维、常规解法，那必将引导考生走向高考成功.

二、明晰《考纲》的知识要求，在内化融合中落实目标

《考纲》的知识要求是：要求对所列知识的含义有初步的、感性的认识；对所列知识内容有较深刻的理性认识，知道知识的逻辑关系，能够对所列知识作正确的描述说明并用数学语言表达，能够利用所学的知识内容对有关问题进行比较、判别、讨论；系统地掌握知识的内在联系，能够利用所学知识对具有一定综合性的问题进行分析、研究、讨论，并加以解决.

明晰《考纲》的知识要求，敦促学生加强对课本知识的内化吸收，夯实基础，并牢固地掌握重要的数学思想方法；提醒学生加深对课本例题和习题内在联系的整理融合，形成更加完备的知识网络和方法体系，真正实现课程的三维目标（知识与技能，过程与方法，情感态度与价值观）.

本题从同角三角函数的基本关系式出发，在x=2、4、6时，借用代数公式，进行三角恒等变形，简化f（α）的表达式，再利用正、余弦函数的有界性，估计f（α）的取值情况，通过观察式子的结构特征，品味式子的数据特点，联想类比，合情推理，猜想得出f（α）的取值范围的一般表达，但问题的解决远未结束，猜想正确性的判定，还有待我们进一步探求，整个过程环环相扣、引人入胜.

三、理解《考纲》的能力要求，在探究分析中培养能力

《考纲》的能力要求是：高考考查空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识；强调探究性、综合性、应用性，突出数学试题的能力立意，坚持素质教育导向.

为此，我们在教学中，应强化解题过程的研究，解题方法的提炼，解题思想的渗透，精心设计一题多解、一题多变、多题一解等训练，引导学生观察、联想、讨论、对比、质疑等实践操作，积极探索解决问题的最佳途径，让学生在探究分析中提高应变能力，激发创新潜能.

题源探究 在α∈R、n∈N*的条件下，证明不等式

事实上，因为0≤sin2α≤1，所以当n∈N*时，sin2nα≤sin2α，同理cos2nα≤cos2α，由此可得，sin2nα+cos2nα≤1.

下面只需证明在α∈R、n∈N*的条件下，不等式

探究途径一、在初等数学范畴内，用数学归纳法求证.

当n=1时，命题成立.

由此可见，这道练习题的编制，专家是煞费苦心的，把题目的基础部分放在必修4，把深入探究的内容植入选修2-2，循序渐进，螺旋上升，体现出开放性、探究性的新课程理念，而数学归纳法是《考纲》中规定考查的内容，应引起我们高度重视.

探究途径二、在高等数学观点下，用凸函数性质解题.

当n∈N*时，构造函数F（x）=xn（x≥0），求其二阶导数，即得F″（x）=n（n-1）xn-2≥0，因此，函数F（x）=xn区间［0，+∞）上是一个下凸函数.

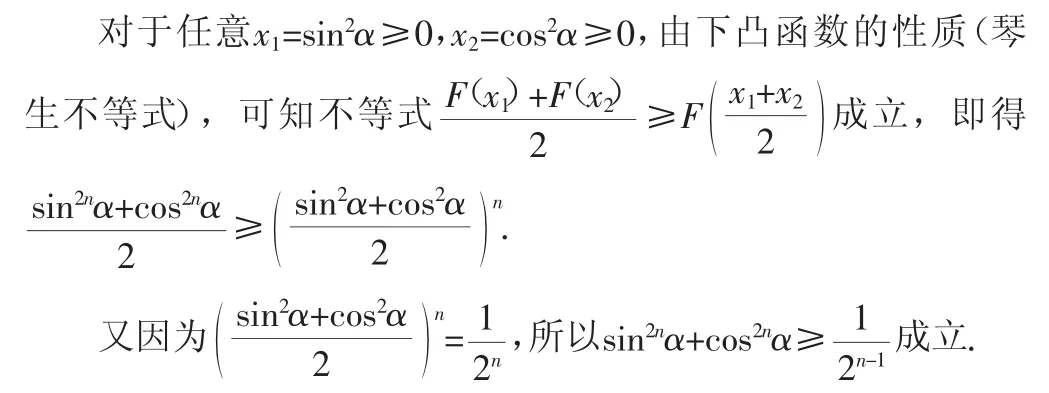
从对题源的探究分析，可知在不同的背景下，运用不同的知识，从不同的角度思考，得到不同的解法，体现出不同的能力要求.

四、体味《考纲》的考查要求，在变式拓展中增长见识

《考纲》的考查要求是：注重试题的基础性、综合性和层次性，坚持多角度、多层次的考查；对数学思想和方法的考查与数学知识的考查结合进行，考查时，从学科整体意义和思想含义上立意.

《考纲》的考查要求告诫我们：对于问题的探究，绝不能浅尝辄止，以得到答案为满足，而应为此作进一步挖掘、多方位求索、有机演变和拓展引申，求新求异，在变式中求拓展、在拓展中觅规律，提高学生分析问题和解决问题的能力，培养学生良好的思维习惯.

从式子sinρα+cosρα的结构看，与题源相似，而sin2α+cos2α=1，且因此转换思考角度，可令

该题源的探究也可另辟蹊径，构造函数g（x）=xn+（1-x）n（0≤x≤1），研究性质加以证明，这样一来，学生就会在问题的解决中，丰富思路、开阔眼界、增长见识.

题源拓展 若a>0，b>0，λ∈R，且λ≠0，λ≠1，满足aλ+bλ=m，那么：

这是《数学通报》第1792号数学问题，乍一看，aλ+bλ=m的结构与题源没有关联，但仔细观察结论，又似曾相识，经过转换，就现庐山真面目.

结合实例，研习《考纲》，我们更加明确高考试题是如何体现在数学知识网络的交汇点和能力层次的交叉区处命题的，也更加明确高考试题是如何多视点、多角度、多层次地考查考生的数学素养和潜能的，同时还知道高考试题的设计总是在想办法客观地反映考生的数学视野、审慎思维的习惯和坚忍不拔的科学态度的.