巧用数形结合思想的解题探究

☉浙江省三门县城关中学 牟雪珍

巧用数形结合思想的解题探究

☉浙江省三门县城关中学 牟雪珍

数形结合思想在新课程背景下，有其广阔的应用空间.数与形是数学中两个最基本的研究对象，每一个形都蕴涵着一定的数量关系，而数又常常可以通过图形做出直观的描述和反映.“数无形少直观，形无数难入微”，数形结合就是把抽象的数量关系和直观的几何图形有机地结合起来.这主要包括两方面的内容：一是“以形助数”，即数量关系借助于图形及其性质使之直观化、形象化，从而获得解题方法；二是“用数解形”，即将几何图形的问题经过数量化描述，借助代数计算获得解题方法.

数形结合 以形助数 用数解形

数形结合思想在新课程背景下，有其广阔的应用空间.“数”与“形”是数学中两个最基本的研究对象，每一个“形”中，即每一个几何图形中都蕴含着一定的数量关系，而“数”中又常常可以通过几何图形做出直观的描述和反映.“数无形少直观，形无数难入微”，数形结合就是把抽象的数量关系和直观的几何图形有机地结合起来.就初中数学而言，数轴建立起实数与数轴上点之间的一一对应关系，使得一元代数式与一元方程、不等式有了直观的几何意义；平面直角坐标系建立起有序实数对与平面上的点之间的一一对应的关系，使任何一个二元方程或不等式都与平面曲线或平面区域相对应，函数及其图像诠释了这种对应关系.另外线段的长度、平面图形的面积、角的大小以三角函数度量等又从另一角度勾勒了数与形的有机结合.在数与形转换的理论基础上自然地产生了数形结合的解题策略：一是“以形助数”，即数量关系借助于图形及其性质使之直观化、形象化，从而获得解题方法；二是“用数解形”，即将几何图形的问题经过数量化描述，借助代数计算获得解题方法.

一、以形助数

“以形助数”，即将代数问题转化成几何图形问题，由图形性质的启示抓住问题的本质，以达到解决问题的目的，从而提高分析问题、解决问题的能力.

1.利用数轴将代数问题转化成几何图形问题

例1 解不等式|x－3|－|x+5|＞2.

分析：题中抽象的数字－5，3用数轴上的点A，B来表示，|x－3|、|x+5|分别表示点X到点B、A的距离.设有一点X1，使X1B－X1A=2，由图1可知X1表示数－2，而|x－3|－|x+5|＞2表示X1B－X1A＞2，则X在X1左侧，所以原不等式的解集为x＜－2.

此类题利用绝对值在数轴上的几何意义，利用数形结合思想，省去了分段讨论的过程，达到以简驭繁的目的.

2.利用函数图像将代数问题转化成几何问题

利用函数图像求解方程及不等式，我们首先应该掌握函数图像（如y=kx，y=k/x，y=kx+b，y=ax2+bx+c）的几何意义，具体到k，b的几何意义.

例2 若方程x2+（m+2）x+3=0的两根均比1大，求m的取值范围.

图2

此类题是方程实根分布的图像解法，利用与已知方程相应的函数图像来确定实根的分布.用数形结合的方法沟通了方程、不等式、函数和函数图像之间的联系，融知识、思想、方法为一体，有利于培养学生的思维能力和综合运用知识的能力.

3.利用图形的边长、面积等将代数问题转化成几何问题

利用图形的面积相等关系，渗透数形结合思想，进一步验证数学公式.让学生体会代数和几何的内在联系，学会从不同的角度分析问题，培养发散思维.

分析：此题直接证明很困难，考虑到左边是两个因式乘积之和的形式，而两因式乘积通常与几何中面积的度量有关，因此考虑构造几何图形来解决.

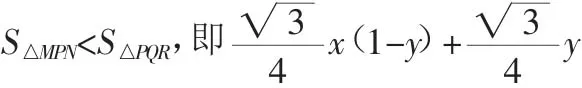
图3

此题是构造等边三角形来证不等式问题.等边三角形、等腰三角形、等腰直角三角形、直角三角形等一些特殊图形，有着特殊的性质，边和角之间具有一定的量化关系.解题时往往构造这些图形来解代数问题，使问题变得直观、形象.

阶梯法是一种结构访谈法，有硬阶梯法与软阶梯法两种形式。本文采用硬阶梯法，即通过编辑结构式问卷，通过特定的指令，让受访者选择产品属性再选择这些属性所能带来的结果，并进一步获得被访问者使用产品的最终目的，即个人价值观，形成“由下而上”的阶梯。

二、用数解形

“用数解形”，即通过“形”的外表，揭示其内在的数量特征，探讨“数”与“形”的本质联系和规律，将几何图形问题经过数量化描述，借助于代数变形获得解题方法.

1.利用坐标解决平面几何问题

此类问题要充分利用直角坐标系这个数形结合的重要载体，它使平面几何的点与坐标系中的一个有序实数对建立一一对应关系.使平面图形中的点加以量化，准确地反映出来.

例4 如图4，E是正方形ABCD内一点，且AE=DE，∠DAE=∠ADE=15°.

求证：△CBE是等边三角形.

证明：以B为原点，BC、BA所在直线为x轴、y轴，建立直角坐标系（如图），设正方形边长为a，可知△EBC各顶点坐标为：

图4

由两点间距离可求得EB=EC=a，所以△CBE是等边三角形.

此题利用直角坐标系，把图形中的点用准确的坐标来表示.

2.利用方程（组）解决平面几何问题

例5 如图5，在△ABC中，D为AB上点，DE∥BC，交AC于点E，设S△ABC=S，S△BDE=S′，求证：S≥4S′.

证明：设DE=x，BC=a，作EF∥AB交BC于F，则BF=x.

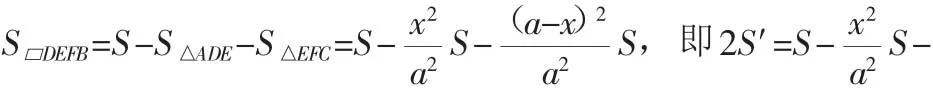
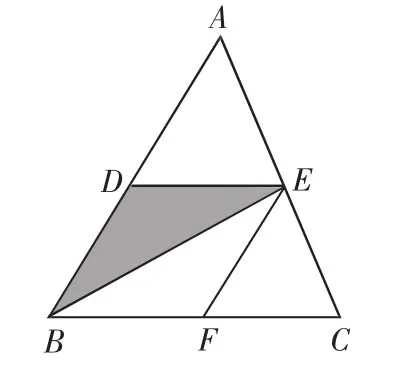
图5

又因为x为实数，所以Δ=4a2S2－16a2SS′≥0，即S≥4S′.

构造二次方程后，可利用违达定理和判别式等进行解题.许多平面几何问题可以通过设元转化成方程问题，比如直角三角形中，根据勾股定理和等积法列出方程.近几年的中考试题中，矩形的翻折问题已成为一个热点，实质上翻折问题是一个轴对称问题，根据翻折前后的对应线段和对应角相等，利用方程模式去解决.还可以利用相似图形的相似比和面积比等列方程，动态几何问题中的边长经常用未知数来表示，根据题目中的数量关系利用方程或函数建模来求解.

3.利用函数解决平面几何问题

例6 △ABC中，∠A=90°，∠C=30°，AB=1，两个动点P、Q，同时从点A出发，P沿AC运动，Q沿AB，BC运动，结果两个动点同时到达点C，求点Q在BC上运动时，△APQ的面积的最大值.

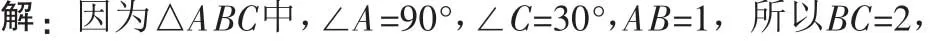
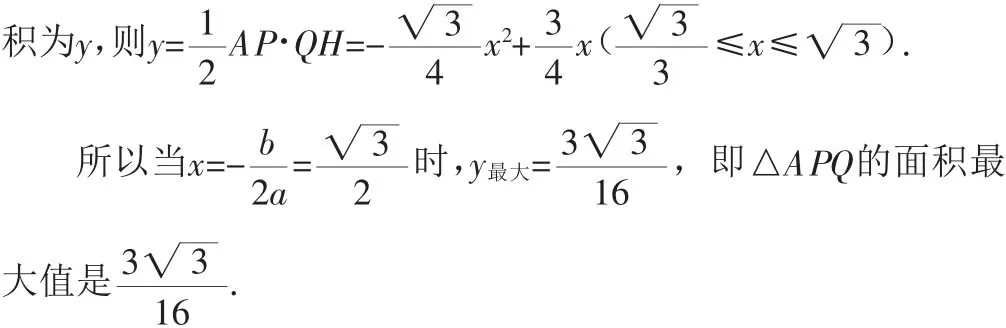
图6

此题是用代数方法解平面几何问题，把面积的最值问题转化成二次函数的最值问题，通过具体的数量关系确定点在图形中的位置，充分体现了数形结合思想.

“数”与“形”两者间是互为条件、互相渗透、互相促进的相辅相成的关系，分开是为了对某一方面的本质更深入的研究，结合是对两者更全面的认识.著名科学家拉格朗日曾经说过：“只要代数同几何分道扬镳，它们的进展就缓慢，它们的应用就狭窄，但是当这两门科学结合为伴侣时，它们就互相吸取新鲜的活力，从那以后，就从快速的步伐走向完善.”

1.吴宝莹.数无形少直观，形无数难入微.赵小云，主编.数学教学论文集.

2.卢建状.证明不等式的数学模型方法.中学数学研究，1995.

3.程时平.抛物线的位置关系符号相关的中考试题浅析.数学教师，1998（3）.

4.葛金良.浅谈构图法在三角函数中的应用.中学教研，1995（11）.