基于DSGA的航空作战平台作战联盟形成策略

张 磊， 姚佩阳， 侯春雷， 张杰勇

(1.空军工程大学信息与导航学院，西安 710077; 2.中国人民解放军71901部队，山东 聊城 252000)

0 引言

信息和网络技术的迅猛发展及其在军事领域的广泛应用，使得未来战场环境日趋复杂，作战平台日益多样。战争对抗双方为了获取体系对抗的整体优势，既要保证聚焦使用作战力量，又必须根据战场态势能够敏捷地调整配置作战资源。单个平台限于自身能力，往往难以独立完成复杂的作战任务，而传统的多平台作战编组限于体制编制模式、作战思维以及随机处置的权限设置等问题，不适合分布式网络化条件下实施敏捷作战的要求。因此，具备不同作战属性的多作战平台根据任务的需要，快速而有效地组成作战联盟将是未来分布式网络化战争一种重要的作战样式。多种作战平台根据作战任务如何形成“作战联盟”成为指挥控制领域一个新问题。

在多 Agent系统(Multi－Aagent System，MAS)中，许多学者对任务联盟形成方法和策略进行了系统深入的研究［1－7］，这为本文航空作战平台联盟形成(Aerial Combat Platform Coalition Formation，ACPCF)问题的研究提供了重要理论技术和方法参考。但是，MAS中任务联盟的形成与ACPCF问题存在几点差异:一是MAS中Agent多是自私或是理性自私的，任务联盟形成的本质是各Agent为获取更多的个体利益而采取的博弈策略，如果将航空作战平台(ACP)看成Agent，该类型Agent属于无私型的，为服务全局不计个体牺牲;二是MAS中Agent倾向于执行计算任务，任务一结束可立即加入下一任务中，任务联盟稳定性较差，随时可能进行联盟重构，而ACP型的Agent完成一项任务后会有一定损耗，同时所形成的作战联盟必须具备一定的鲁棒性。基于以上分析，本文在MAS任务联盟形成理论基础上，针对ACP的特点，分析建立ACPCF问题的数学模型，并针对该模型利用一种双串编码遗传算法(Double Strings Genetic Algorithm，DSGA)对问题进行求解。

1 问题描述

1.1 作战联盟的相关概念

为了更好地描述ACP作战联盟的形成问题，首先给出该问题相关概念的基本定义。

定义1 作战平台(Combat Platform):在该问题中是指航空作战平台，是资源能力的载体，为执行作战任务提供武器装备、通信设施、侦察监视设备等资源，主要包括预警机、歼击机、电子战飞机等。在本文问题中，假设形成作战联盟可使用的作战平台集合为:P={P1，P2，…，Pj，…，PK－1，PK}，K 表示作战平台集合中平台的数量;作战平台 Pj所拥有的资源能力向量PAj=(rj1，rj2，…，rjl，…，rjL－1，rjL)，rjl用于定量描述 Pj所具备的第l项类型的资源能力的大小。

定义2 作战任务(Combat Task):是由ACP作战的使命环境决定的，是作战联盟形成并进行所有活动的依据和目标，作战任务通常是需要一定资源能力才能完成的活动。在本文问题中，假设需要完成的作战任务为T;该作战任务T的资源能力需求向量为RA=(R1，R2，…，Rl，…，RL－1，RL)，Rl用于定量描述成功处理任务T所需第l项类型的资源能力的大小。

定义3 作战联盟(Combat Coalition):是根据ACP所需执行的作战任务需要，从可选择的作战平台集合中挑选一定的平台，按照一定的协议和规则组成的作战平台的联合体，该联合体可以通过有效的任务分配和计划协调完成作战任务中的各个作战目标。作战联盟因作战任务的存在而产生，也随着作战任务的完成而解散。在本文问题中，假设作战联盟C的资源能力向量为CA=(S1，S2，…，Sl，…，SL－1，SL)，Sl用于定量描述作战联盟CA所具备的第l项类型的资源能力的大小，其数值为

1.2 问题建模

为了准确描述ACPCF问题的数学模型，先对问题作如下假设。

假设1 假设作战联盟形成过程中，只考虑作战平台资源能力对作战联盟形成的影响，而忽略其他因素对其的影响。

假设2 假设作战联盟形成是在一个非超加性环境中(超加性是指对于任意两个独立的作战联盟，若将它们合并为一个作战联盟，其收益大于等于这两个作战联盟收益之和)，否则，最大的作战联盟(包括所有作战平台)将是最有益的［8］。

1.2.1 目标函数

ACP形成作战联盟的基本要求:1)确保能够完成作战任务(即满足作战任务的资源能力需求);2)作战联盟的成本尽可能小。联盟成本(OC)一般有两部分组成:资源能力成本(FC)和平台协作成本(CC)。

资源能力成本是组成作战联盟的所有作战平台总的资源能力折合的成本。资源能力成本通常也可以用作战联盟的资源能力的冗余来表示，即作战联盟所拥有的作战平台资源能力正好满足作战任务的资源能力需求时，该作战联盟的资源能力成本最小。即

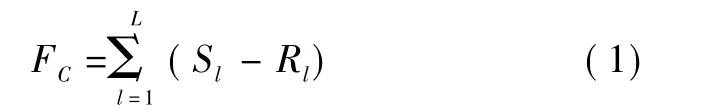
平台协作成本是在作战联盟形成过程中，期望减少作战联盟中作战平台在任务执行时不必要的协作，即如果某一作战平台的资源能力能满足作战任务的资源能力需求，就不用选择多个作战平台来协作完成这一任务。因此，作战联盟中的作战平台的数量越多，该作战联盟中作战平台之间的协作成本就越大。在本文问题中，假设作战联盟形成问题的平台协作成本与联盟中平台的数量的平方成正比。即

其中，N(C)表示作战联盟C中作战平台的数量。

因此，联盟成本OC为资源能力成本FC和平台协作成本CC的加权和。即:

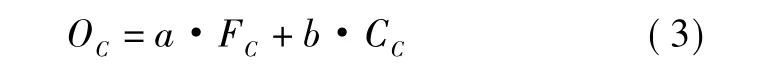
其中，a和b为权系数，表示对应成本对总成本的影响。

ACPCF问题的目标函数就是极小化联盟成本OC。

1.2.2 问题的约束条件

在本节假设条件的基础上，ACPCF的约束条件只有一个，即作战联盟的资源能力要满足作战任务的资源能力需求，也就是说作战联盟的每一项类型的资源能力必须大于等于作战任务对应项类型的资源能力需求，这也是作战联盟形成的必要条件。可以表示为

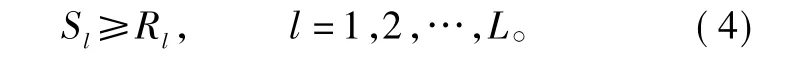
1.2.3 问题的数学描述

综合上述ACPCF问题的目标函数和约束条件，该问题的数学描述为

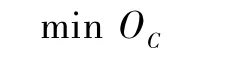
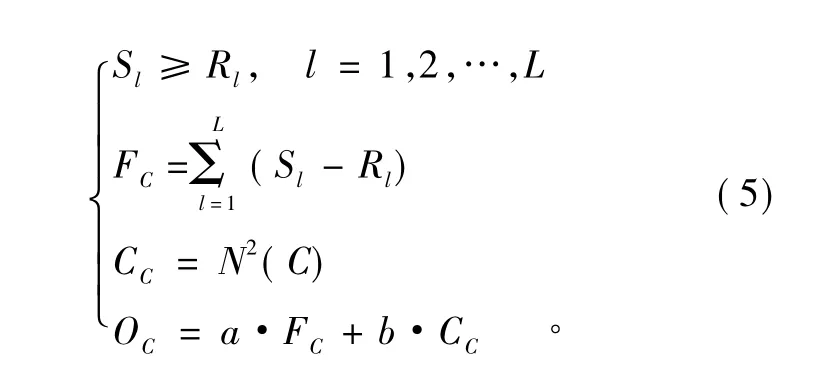
2 问题求解

由式(5)可知，该问题实质上是一个复杂组合优化问题，即是一个非确定性多项式时间(Nondeterministic Polynomial，NP)问题。本文采用遗传算法(GA)来求解以上问题模型。GA是由美国 Michigan大学的 J.Holland教授创建的一种概率搜索算法，它是利用某种编码技术和遗传运算机制来求解复杂的优化问题［9］。

2.1 染色体的编码和解码方式

为了简化使用GA求解带约束优化问题的难度，针对式(5)问题数学模型的特点，本文使用DSGA对染色体进行编码［10］。如图1所示。

图中:Z(i)(i=1，2，…，K)表示作战平台的标号，取值范围为{1，2，…，K}，对应可使用平台集P中的作战平台，而序列［Z(1)，Z(2)，…，Z(K)］为1～K 的一个随机序列;FZ(i)是标号为Z(i)的平台所对应的状态取值，取值范围为{0，1}。

这种双串结构的编码方式，特定的解码方式产生的原象总为可行解(在解码过程中考虑问题模型的约束条件)，从而可以提高GA的进化效率，以下为这种双串结构染色体的解码方式。

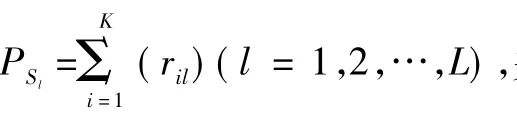
2) 设解码后产生的原象为(G1，…，Gj，…，Gk)(j=1，2，…，K)，Gj表示标号 j的作战平台的真实状态。

3)设i=1。

4)如果 FZ(i)=1，则 GZ(i)=1，执行 6);如果FZ(i)=0，执行5)。

6) 如果∀l∈{1，2，…，L} s.t.P'S≥Rl，则

l0;否则

7)i=i+1，假如 i＞ K，结束循环;否则，执行4)。

2.2 适应度函数

由式(5)可得，问题数学模型的目标函数为极小化作战联盟形成的联盟成本OC，因此，本文设计的DSGA的适应度函数为联盟成本OC的逆，即

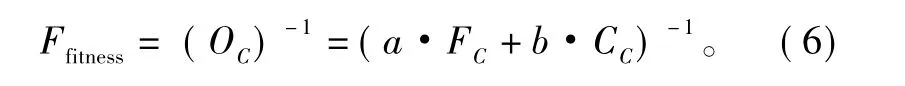
2.3 遗传算子

1)交叉算子。

对于这种双串结构的染色体编码方式，如果采用传统的单点或多点交叉方式进行交叉运算，在产生的子代染色体中的序列［Z(1)，Z(2)，…，Z(K)］一般不为1～K的随机序列(一般会出现相同的作战平台标号)，使得子代染色体的编码方式不可行。因此，针对双串结构的染色体编码方式，本文采用部分匹配交叉(Partially Matched Crossover，PMX)［11］进行交叉运算，以下为这种双串染色体编码方式使用PMX进行交叉操作的具体过程。

① 初始化，设种群规模为SD，并设i=1。

②从父代染色体种群中任意选择两个染色体X和 Y，同时令 X'=X，Y'=Y。

③ 产生一个随机数 ra，ra∈［0，1］，如果 ra≤Pc(Pc为交叉概率)，执行④ ;否则，执行⑨ 。

④ 从序列(1，2，…，K)中随机产生两个交叉点u和v(u≠v)，令 d=u，首先对 X'和 Y执行⑤ ～⑦的操作。

⑤ 令j=((d－1)%K)+1(其中(d－1)%K表示整数(d－1)除以整数 K的余数)，寻找 j'，使得ZX'(j')=ZY(j)，交换(ZX'(j)，FZX'(j))T和(ZX'(j')，FZX'(j'))T，d=d+1。

⑥ 如果u＜v，当d＞v时，执行⑦;当d≤v时，执行⑤;如果 u＞v，当 d＞(v+K)时，执行⑦;当 d≤(v+K)时，执行⑤。

⑦ 如果 u＜v，使 FZX'(j)=FZY(j)(u≤j≤v)，执行⑧;如果 u ＞ v，使 FZX'(j)=FZY(j)(1≤j≤v，u≤j≤K)，执行⑧。

⑧ 同样，对Y'和X执行⑤～⑦的操作。

⑨ 得到的X'和Y'就是两个父代染色体X和Y的子代。

⑩ i=i+1，假如 i≤SD，执行①;否则，停止。

初始种群通过交叉算子可以得到规模为2·SD的新的种群，称这个新的种群为交叉种群。

图2为PMX的一个例子，描述了X'和Y的交叉过程。

2)变异算子。采用均匀变异(Uniform Mutation，UM)的方法进行变异操作，具体步骤如下。

① 设i=1。

② 设j=1。

③ 产生一个随机数 ra，ra∈［0，1］，如果 ra≤Pm(Pm为变异概率)，执行④;否则，执行⑤。

④ 如果FZ(j)=1，则令 FZ(j)=0;如果 FZ(j)=0，则令FZ(j)=1。

⑤ j=j+1，如果j≤K，执行③ ;否则，执行⑥。

⑥ i=i+1，如果i≤SD，执行① ;否则，停止。

初始种群通过变异算子可以得到规模为SD的新的种群，称这个新的种群为变异种群。

3)选择算子。

常用的GA的选择算子较多，如精英策略(Elitism)、赌轮选择(Roulette Wheel Selection)、期望值选择(Expected Value Selection)等。本文将原始种群、交叉种群和变异种群中的个体合并为一个种群，这个种群的规模为4·SD，称这个种群为合并种群。采用2.2节中计算适应值的方法，使用精英策略和赌轮选择相结合的方法对合并种群进行选择操作。包括两方面:精英主义和赌轮选择。

精英策略:如果上一代种群中的个体的适应度大于这一代种群中的每一个个体，则将它保留到这一代种群中。

赌轮选择:个体的选择概率与其适应性成比例，对新一代种群中的另外SD－1个个体通过对合并种群进行SD－1次轮盘赌选择的方式产生。

4)停止准则。

本文的停止准则采用最大迭代数进行判断，即判断迭代的代数是否达到要求，如果群体进化已趋于稳定，则选择最优的染色体个体作为该问题模型的优化解输出。

2.4 算法步骤

DSGA的流程如图3所示。

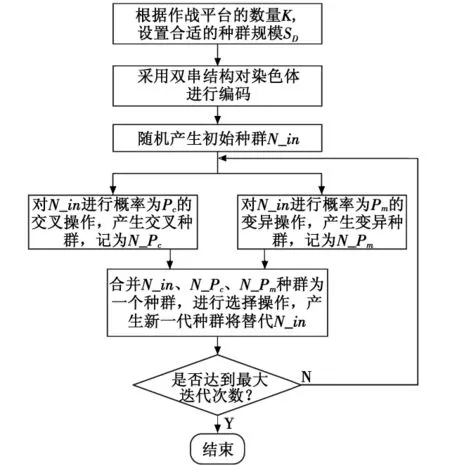
图3 DSGA的基本流程图Fig.3 Basic flow chart of DSGA

3 算例分析

本文以一个航空兵突击作战的想定为案例，在Inter(R)Pentium(R)4 CPU 3.00 GHz计算机上进行仿真实验。

案例想定中的假设作战任务T为航空兵突击任务，其所需的资源能力如表1所示。可使用的作战平台集P为{P1，P2，…，P15}，其资源能力属性如表2所示。其中，表1和表2中的8维资源能力分别为{预警监视，指挥控制，电子干扰，空中通信，空中掩护，压制防空，空中对抗，对地打击}。

表1 作战任务的属性Table 1 Attribute of combat task

表1中Rl的取值表示任务T的第l项类型的资源能力需求的大小，其数值越大，能力需求越大;表2中Pj的取值表示作战平台所具备的第l项类型的资源能力的大小，其数值越大，完成该项类型任务的能力就越强。

针对以上仿真案例，作了以下仿真实验。

仿真实验1 设置DSGA中的参数SD=10，Pc=0.7，Pm=0.05，迭代次数为50次，设置模型中的参数a=3和b=1。使用本文设计的DSGA求解以上案例，得到的DSGA的收敛曲线，如图4所示。

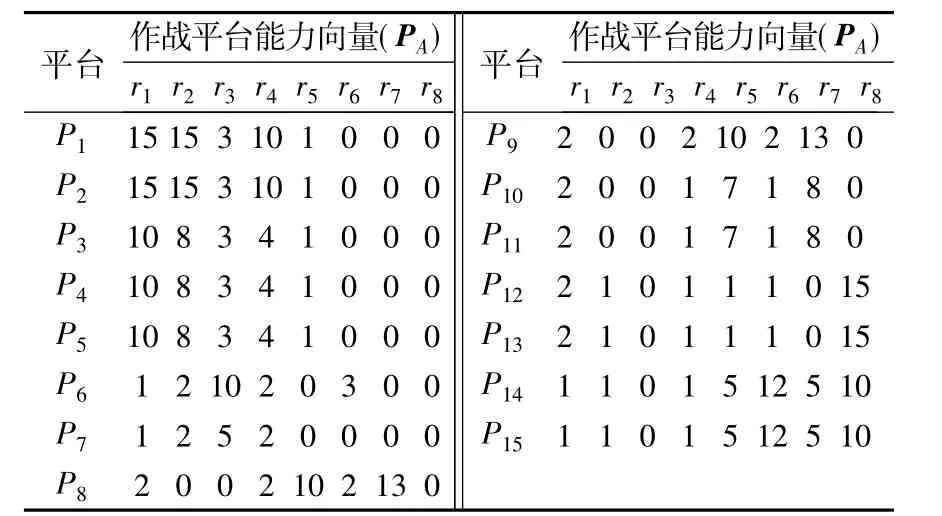
表2 作战平台资源的属性Table 2 Attribute of combat platform resources

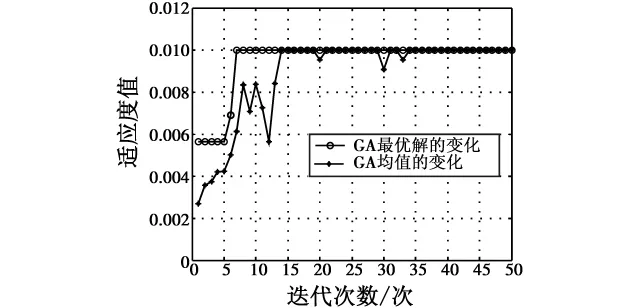
图4 DSGA的收敛曲线Fig.4 Constringency curve of DSGA

由图4可得，以上案例的最优的适应度值为Ffitness，best=0.0100。

对应的染色体的编码和解码方式分别如图5中a和b所示，由案例的求解结果可得，最佳的作战联盟为

图5 最佳的染色体编码和解码形式Fig.5 The optimum chromosome coding and decoding method

仿真实验2 设置循环次数为60次，得到的结果如图6所示;作战平台数量不同情况下的算法运行时间如表3所示。可以看出，算法具有较好的可靠性和时效性，实验的结果比较满意。

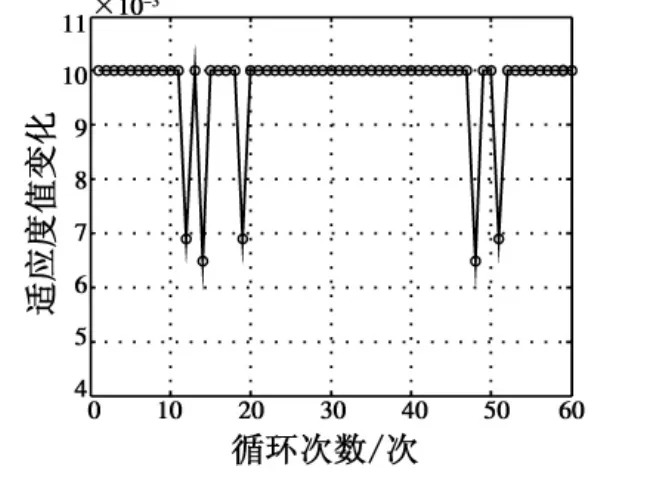
图6 最佳适应度值变化曲线Fig.6 Change curve of optimal fitness value

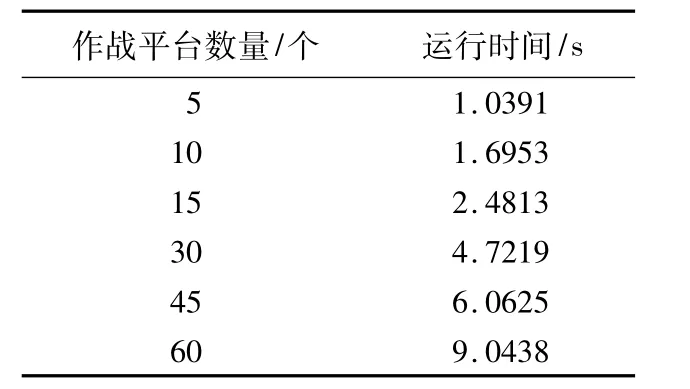
表3 不同作战平台数量情况下的算法运行时间Table 3 Time cost of the algorithm with different quantity of combat platforms

4 结论

本文针对分布式网络化战争中作战资源可以自由组合、柔性配置度高等新特点，提出作战联盟的新作战理念，并重点对联盟形成策略进行了研究。从任务资源能力需求与平台属性能力优化匹配的角度建立了作战联盟形成问题模型，并利用改进的遗传算法对模型进行求解。仿真实验结果证明了算法能很好地解决联盟形成问题，并且具有良好的可靠性和时效性。

［1］ 常勇，吴庆宪，张立珍，等.基于MAS的无人机纵向飞行控制［J］.电光与控制，2011，18(3):21－24.

［2］ 傅一峰，曹健，李明禄.面向复杂任务结构的Agent联盟算法［J］.小型微型计算机系统，2011，32(3):402－406.

［3］ 许波，余建平.基于量子遗传算法的多任务联盟并行生成算法［J］.计算机应用研究，2010，27(6):2100－2102.

［4］ 蒋建国，吴琼，夏娜.自适应粒子群算法求解Agent联盟［J］.智能系统学报，2007，2(2):69－73.

［5］ ZHENG S F，HU S L，LAI X W，et al.Searching for agent coalition using particle swarm optimization and death penalty function［C］//LNCS 4681，Springer－Verlag，Heidelberg，2007:196－207.

［6］ 蒋建国，李勇，夏娜.一种求解单任务Agent联盟生成的贪婪算法［J］.系统仿真学报，2008，20(8):1961－1964.

［7］ 夏娜，蒋建国，魏星，等.改进型蚁群算法求解单任务Agent联盟［J］.计算机研究与发展，2005，42(5):734－739.

［8］ HARSANYI J C.A simplified bargaining model for n－person in games and social situations［M］.Cambridge University Press，1997.

［9］ 王玮，程树昌，张玉芝.基于遗传算法的一类武器目标分配方法研究［J］.系统工程与电子技术，2008，30(9):1708－1711.

［10］ SAKAWA M，KATO K.Genetic algorithms with double strings for 0－1 programming problems［J］.European Journal of Operational Research，2003，144:581－597.

［11］ 王小平，曹立明.遗传算法——理论、应用与软件实现［M］.西安:西安交通大学出版社，2002:28－38.