基于微分进化的组合重采样粒子滤波算法

王龙生， 顾 浩， 余云智

(江苏自动化研究所，江苏 连云港 222006)

0 引言

近年来，粒子滤波(Particle Filter，PF)［1－2］因适用于任何能用状态空间模型表示的非高斯背景的非线性随机系统，精度可以逼近最优估计，是一种很有效的非线性滤波技术而备受关注，被广泛应用于计算机视觉、信号处理、定位导航及目标跟踪等诸多工业领域［3］。

粒子滤波的核心思想是通过从后验概率中抽取的随机状态粒子来表达其分布，是一种顺序重要性采样方法。该算法存在的最主要的问题是需要用大量的样本数量才能很好地近似系统的后验概率密度。另外，重采样阶段会造成样本有效性和多样性的损失，导致出现样本贫化现象［4－5］。如何保持粒子的有效性和多样性，克服样本贫化，一直是研究的重点。

为了解决多样性损失问题，文献［6］针对重采样算法的改进提出了遗传重采样粒子滤波算法，通过引入遗传交叉变异操作，在一定程度上解决了样本贫化问题，但是遗传算法实时性不好，在工程应用上还有待提高。微分进化(Differential Evolution，DE) 算法［7］，是一种采用浮点矢量编码的连续空间中进行随机搜索的优化算法，已被证明在许多优化问题中都表现出优于自适应模拟退火算法、粒子群算法、遗传算法的性能［8］。本文通过引入微分进化算法进行重采样，利用其交叉变异操作创造更多的粒子，增加样本多样性，抑制退化现象，并将微分进化重采样和残差重采样进化组合优化，解决算法实时性的问题，蒙特卡罗仿真表明此方法的有效可行性。

1 粒子滤波

粒子滤波是一种基于蒙特卡罗方法和贝叶斯估计的统计滤波方法，它首先依据系统状态向量的经验条件分布在状态空间产生一组随机样本(粒子)，然后根据量测不断调整粒子的权重和位置，通过调整后的粒子信息修正最初的经验条件分布。

为了得到正确的状态估计，通常希望粒子权值的方差尽可能趋近于零，然而，序贯蒙特卡罗模拟方法一般都存在权值退化问题。在实际计算中，随着滤波迭代次数的增加，粒子权值的方差随着时间增大，状态空间中的有效粒子数较少，即当滤波一段时间后，粒子的权值会出现两极分化，少数粒子具有很大的权值，对结果起主导作用，而其余大多数的粒子权值很小，对结果几乎没有影响，从而使得大量计算浪费在求解几乎不起任何作用的粒子的更新上，结果粒子集无法表达实际的后验概率分布，这就是粒子滤波算法的退化问题。一般通过引入重采样算法基本上消除了粒子滤波算法的退化现象，但是重采样算法带来的另一个问题是粒子样本枯竭。以上诸多因素严重贫化了样本支撑集，极大地影响了估计结果，不利于状态估计与跟踪，当估计那些在很长时间维持不变的量时，退化现象更为严重。因此，一个好的重采样算法应该在减少权值较小的粒子数目和增加粒子样本多样性之间进行有效折衷。

2 组合进化重采样算法

2.1 微分进化重采样

使用一般重采样算法，粒子多样性损失是不可避免的，本文通过引入微分进化算法进行重采样，经过交叉变异操作在一定程度上可以克服粒子滤波的样本贫化问题。微分进化算法具有高效性、收敛性、鲁棒性等优点［9］，相比于遗传算法，它保留了基于种群的全局搜索策略，采用实数编码、基于差分的简单变异操作和一对一的竞争生存策略，降低了遗传操作的复杂性。微分进化重采样算法中交叉、变异操作定义如下［10］。

1)交叉算子。

在DE中，执行交叉运算可以增加种群多样性。常见的有二项交叉和幂交叉。由下式计算交叉向量

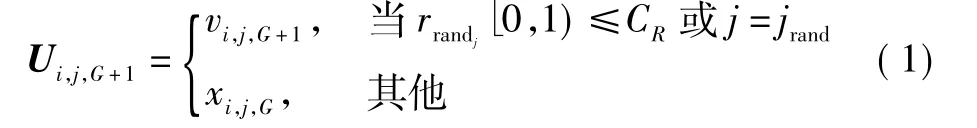
式中:CR∈［0，1］;jrand∈{1，2，…，N}，j=1，2，…，N。CR为交叉概率，CR越大，DE收敛越快;CR值越小，DE鲁棒性越好，但增加了执行时间。

2)变异算子。

目标向量表示为 Xi=(x0，i，…，xN－1，i)T;变异向量表示为 Vi=(v0，i，…，vN－1，i)T，i=0，1，…，NP－ 1;N 为目标向量的维数;NP为种群数。常用的变异操作为(下标G表示第G代)

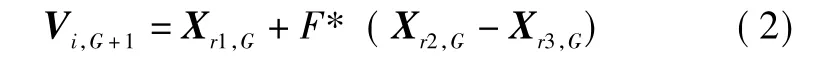
式中:r1，r2，r3∈{1，…，NP}，为互不相等的整数，且它们与i不相等;F∈(0，1)，用于控制变异比例。

微分进化粒子滤波流程如图1所示。

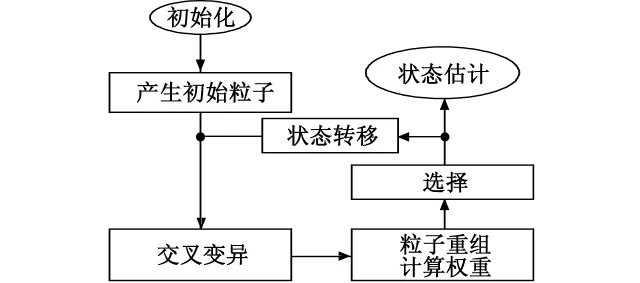
图1 微分进化粒子滤波流程图Fig.1 Flow chart of the different evolution particle filter

微分进化重采样算法步骤如下。

①初始化采样。

从初始分布p(x0)中采样N个粒子样本集xi0，i=1，2，…，N。

②微分进化操作。

将N个粒子作为粒子初始种群，利用式(1)和式(2)进行交叉变异处理，得到N个新样本，将原始样本集与新样本合并为大小为2N的候选集。

③状态估计。

将权值大于w0的样本组成一个集合，取其均值作为预测值。w0为常数。

④粒子重采样。

计算候选集中各样本的权值wi，并降序排序，选择前一半作为下一代种群。

⑤粒子更新。

进入下一时刻，粒子进行系统状态转移，然后转至步骤②。

2.2 残差重采样

针对标准粒子滤波算法存在的权值退化现象，文献［11］提出了自举粒子滤波算法，该算法在递推过程中引入了重采样的思想以克服退化问题。重采样的基本思想是:通过对用粒子和相应权值表示的后验概率密度函数重采样产生新的粒子集，即在满足条件下，将粒子集合更新为。在常用的重采样算法中，残差重采样法具有效率高、易于实现的特点。设其中为取整操作。残差重采样采用新的权值选择余下的个粒子。残差重采样的主要过程有:

3)对于每个μi，寻找归一化权值累计量大于或等于 μi的最小标号 m，即。当 μi落在区间［λm－1，λm］时，被复制一次。这样，每个粒子经重采样后的个数为步骤3)中被选择的若干粒子数目与Ni之和。

2.3 组合算法

样本贫化是粒子滤波算法的一个主要问题，微分进化算法重采样由于引入了微分进化算法的交叉变异操作，获得了更多的可选择粒子，使得粒子的多样性得到保障，从而抑制了粒子退化现象。但同时，由于交叉变异操作带来了一定的实时性问题，因此加大了滤波时间。常用的重采样算法具有简洁、实时性高的特点，其中以残差重采样算法效率最高，本文通过将微分进化重采样算法和残差重采样算法进行组合重采样，从而既保持了粒子的多样性又提高了算法实时性。

对于样本贫化现象，引入有效粒子采样尺度

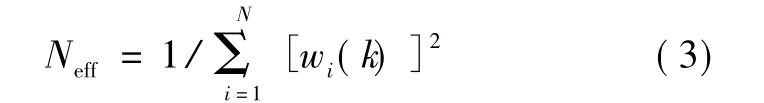
Neff变小，就意味着粒子存在退化现象。如果Neff=1，即一个粒子的权值为1，其他粒子的权值为0，说明粒子退化严重;如果Neff=1/N，则表示每个粒子的权值为1/N，粒子未退化。因此，为了克服样本贫化现象，当Neff低于某一门限值时需要进行多样性恢复。

组合算法流程如图2所示。

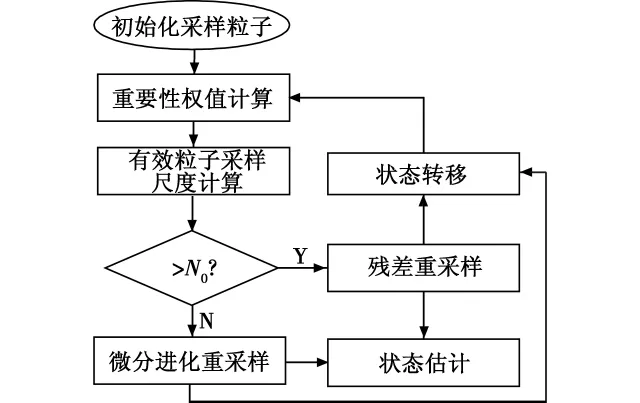
图2 组合算法流程图Fig.2 Flow chart of the combined algorithm

组合算法步骤如下。

1)初始化采样。

从初始分布p(x0)中采样N个粒子样本集xi0，i=1，2，…，N。

2)重要性权值计算。

在k时刻，更新粒子权值

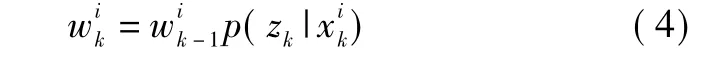
并且归一化

3)有效粒子采样尺度计算。

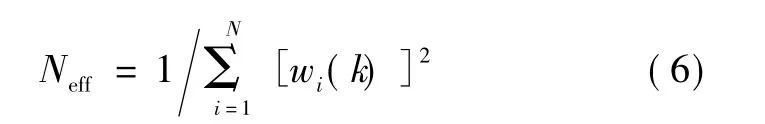
4)重采样算法选择。

设Neff门限值为 N0，当 Neff低于 N0时，转至步骤5);否则转至步骤6)。

5)微分进化重采样。

使用交叉变异操作，增加粒子样本数，进行状态估计和粒子更新，转至步骤8)。

6)残差重采样。

使用残差重采样算法，进行粒子重采样，并行重新分配粒子权值，所有粒子权值为1/N。

7)状态估计。

8)粒子更新。

进入下一时刻，粒子进行系统状态转移，然后转至步骤2)。

3 仿真结果及分析

本文选用粒子滤波器性能评测时常用的一个基准(benchmark)［7］进行仿真，即单变量的非静态经济增长模型，它是计量经济学中常见的问题。该系统具有高度非线性，似然函数呈双峰，使得用传统方法来解决非常困难。

该问题的过程模型和量测模型为

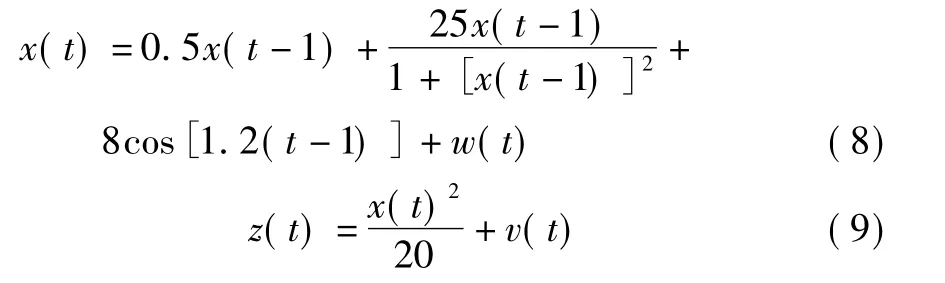
式中，w(t)和v(t)为零均值高斯噪声，方差分别为10与1，初始状态取x(0)=10。

粒子权值计算式为

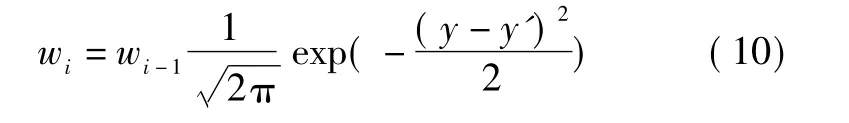
式中:y为观测值;y'为观测的估计。

对标准的基于残差重采样的粒子滤波算法和微分进化粒子滤波算法以及本文的组合算法进行实验，取粒子数目为1000个，采样时间序列为100，交叉概率和变异概率分别为0.95和0.85，种群数 NP为5。程序运行于Windows XP系统，电脑配置为酷睿双核Q8400处理器，2 G内存，运行环境为Matlab 2008。

表1为500次蒙特卡罗仿真结果，其中DE－PF为微分进化粒子滤波算法，RDPF为本文新算法，PF为残差重采样粒子滤波算法。由表1可知，本文算法在精度上要明显优于PF算法，相对于DE－PF精度也有所提高，而且在实时性上，要明显优于DE－PF算法。新算法使用300个粒子可以超过PF算法1000个粒子的精度，并且实时性更好。

表1 运行500次蒙特卡罗仿真的滤波效果对比Table 1 The tracking results of 500 times of Monte Carlo simulation

图3和图4分别为3种滤波算法的滤波效果图和误差对比图。

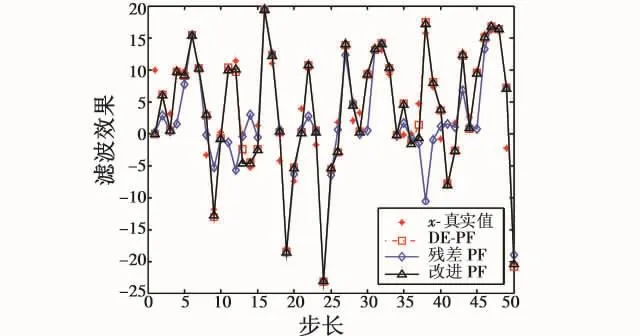
图3 滤波效果对比图Fig.3 The tracking results of different filter

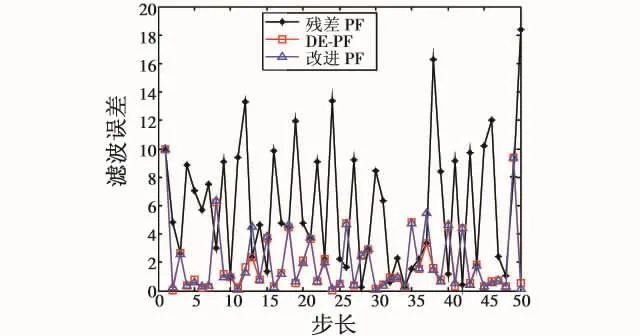
图4 滤波误差图Fig.4 The tracking error of filter estimation

由图可以看出，本文的新算法不仅继承了微分进化重采样算法在精度方面的优点，而且也获得了残差重采样算法的实时性优点，在一定程上产生了更多粒子，抑制了粒子退化现象。新算法具有精度高，实时性好的双重优点。

4 总结

本文的RDPF算法将微分进化重采样和残差重采样有机地结合起来，由于微分进化交叉变异操作创造了新的粒子，在一定程度上增加了粒子的多样性，抑制了粒子退化现象，因此滤波性能有所提高。同时，RDPF算法由于组合了残差重采样算法，算法的实时性得到了一定的提高。仿真结果表明，本文的算法具有精度高和实时性好的优点，应用前景乐观。

［1］ DOUCET A，DE FREITAS J，GORDON N.Sequential Monte Carlo methods in practice［M］.New York:Springer，2001.

［2］ DOUCET A，GODSILL S，ANDRIEU C.On sequential Monte Carlo sampling methods for Bayesian filtering［J］.Statist Computer，2000(10):197－208.

［3］ 姚智颖，刘冬，刘光斌.基于粒子滤波的INS/TAN组合导航［J］.电光与控制，2006，13(3):54－55.

［4］ 夏克寒，许化龙，张朴睿.粒子滤波的关键技术及应用［J］.电光与控制，2005，12(6):1－4.

［5］ 杨德贵，张长城，郑涛.粒子滤波算法的性能分析与改进［J］.电光与控制，2008，15(5):72－75.

［6］ 叶龙，王京玲，张勤.遗传重采样粒子滤波器［J］.自动化学报，2007，33(8):885－887.

［7］ STORN R，PRICE K.Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces ［J］.JournalofGlobalOptimization，Kluwer Academic Publishers，1997，11:341－359.

［8］ 冯琦，周德云.基于微分进化算法的时间最优路径规划［J］.计算机工程与应用，2005，41(12):74－75.

［9］ STORN R.Sytem design by constraint adaptation and differential evolution［J］.IEEE Transactions on Evolutionary Computation，1999，3(1):22－34.

［10］ 苏海军，杨煜普，王宇嘉.微分进化算法的研究综述［J］.系统工程与电子技术，2008，30(9):1793－1797.

［11］ GORDON N，SALMOND D J，SMITH A F M.Novel approach to nonlinear/non－Gaussian Bayesian state estimation［J］.IEEE Proceedings F Radar and Signal Processing，1993，140(2):107－113.