基于滚转角速率的无人机横侧向控制律设计
李春涛, 范淑娜
(南京航空航天大学自动化学院,南京 210016)
0 引言
小型无人机凭借其操作容易、经济实惠、维护方便等特点,受到越来越多人的青睐,近来对小型无人机飞行控制的研究也更加广泛。由于多数小型无人机存在一类似的特点:绕X轴的转动惯量较小,副翼的舵效高,受到扰动后滚转角速率变化非常快,使得其横侧向控制成为飞行控制的难点[1-2]。由于无人机存在这样的特性,使得常规的以滚转角为主要反馈信号、滚转角速率用来增加滚转阻尼的横侧向控制器很难满足设计要求。为解决这一问题,文献[1]采用了动态逆和H∞相结合的方法,设计了滚转角控制器,该控制器具有较强的鲁棒性,但是对模型精度的要求较高,具有一定的局限性,而且反馈线性化的过程相当繁琐,不利于工程上的应用。文献[2]采用神经网络的方法实现小型无人机横侧向航迹跟踪,但在设计过程中,使用多种类型的无人机状态反馈信号,限制了其在工程中的应用。本文在经典PID控制的基础上,利用鲁棒伺服LQR的方法,设计了一种以滚转角速率为内回路的小型无人机横侧向控制律。仿真研究结果表明,基于滚转角速率的控制律能很好地抑制各种干扰的影响,满足样例无人机横侧向控制的要求。
1 问题提出
由动力学方程和运动学方程[3]构成的无人机非线性数学模型,其状态空间描述式为
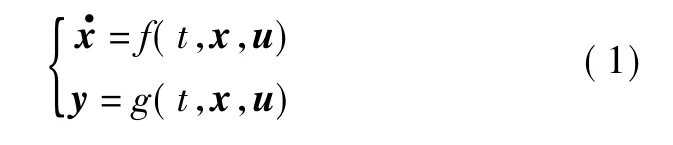
式中:t为时间;x为状态;u为控制输入;y为输出。状态量 x=[φ,θ,ψ,P,Q,R,U,V,W,Xe,Ye,Ze]T,分别为滚转角、俯仰角、航迹角、滚转角速率、俯仰角速率、偏航角速率、机体坐标轴上的速度分量、纵向位移、侧向位移、高度;控制量 u=[δe,δa,δr,δT]T,分别为升降舵偏角、副翼偏角、方向舵偏角、发动机油门开度。以无人机的直线定常无侧滑飞行作为基准运动,利用小扰动方法,得到横侧向线性运动模型为

其中

C 为单位阵;D 为零;状态量 x=[φ,ψ,p,r,v,ye]T;输入量 u=[δa,δr];输出量 y=[φ,ψ,p,r,v,ye]T。
从A阵和B阵中可以看出,样例无人机自身的滚转角速率的衰减率为-2.3(°)/s,而单位副翼引起的滚转角速率变化为-43.0(°)/s,这也表明了样例无人机横侧向转动惯量小、副翼效率高的特点。
2 控制律设计
控制系统一般由控制回路(内回路)和制导回路(外回路)构成。控制回路是外回路控制的基础,其性能优劣直接影响制导回路的控制结果,影响无人机的飞行性能。本文采用鲁棒伺服LQR优化方法设计控制增益,与一般线性二次型(LQR)方法相比,鲁棒伺服LQR方法将积分控制引入到状态反馈中,提高了系统跟踪、抑制扰动的能力[4-7]。
2.1 滚转角速率控制律设计
从样例无人机的线性化模型式(2)中抽取状态x=P,y=P,得到:Ac= -2.2643,Bc= -42.9697,Cc=1,Dc=0。
选取输出信号为滚转角速率P,则跟踪误差表示为

由式(3),将输出信号P跟踪转化为对跟踪误差e的调节。将跟踪误差e增广为系统的状态量,得到新的状态方程为

式(4)中,各变量定义如下

根据LQR优化控制理论,选取性能指标函数
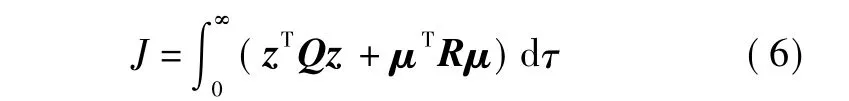
选取合适的性能加权矩阵Q与控制加权矩阵R,解黎卡提方程[6]即可求得控制增益
在选取性能加权矩阵Q与控制加权矩阵R的过程中,由于两者有相对比例关系,将R设置为1。给出性能加权矩阵Q=diag{q1,q2}与时频域控制品质性能的关系,由此确定加权矩阵Q。加权矩阵Q中各项与控制器的超调量、相位裕度、截止频率和回差矩阵奇异值之间的关系见图1,性能加权矩阵Q的选取流程如图2所示。
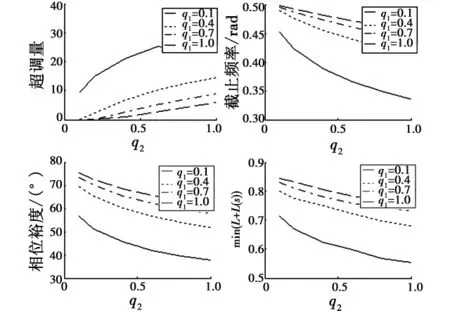
图1 Q与性能指标关系曲线Fig.1 Relationship between Q and performance
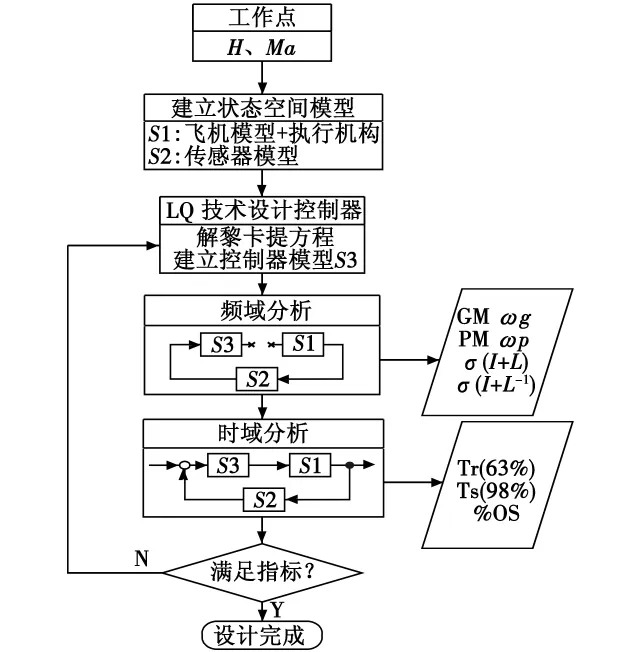
图2 性能加权矩阵Q选取流程Fig.2 Flow chart for selecting performance weighting matrix Q
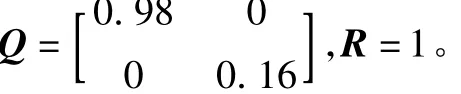
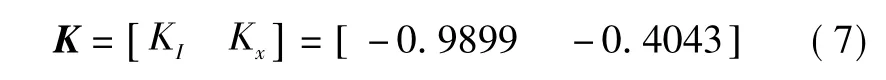
于是有
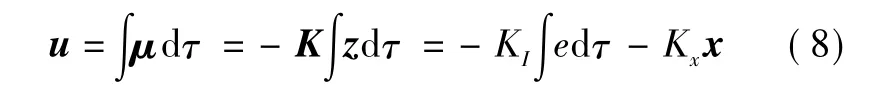
根据式(8)可以得到基于滚转角速率控制器的结构如图3所示。

图3 滚转角速率控制器结构示意图Fig.3 Structure diagram of roll rate controller
滚转角速率控制器的数学表达式为
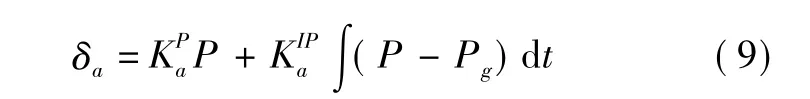
由式(2)~式(8)可知,鲁棒伺服LQR方法通过将控制指令误差增广为新的系统的状态量,利用状态反馈引入积分控制,提高系统型次,消除稳态误差。采用这种结构的滚转角速率控制器时,若无人机受到扰动,积分项的作用会使得滚转角速率迅速回到给定值。
2.2 滚转角控制器设计
图4为滚转角控制器的结构示意。

图4 滚转角控制器结构示意图Fig.4 Structure diagram of roll angle controller
滚转角控制器数学表达式为

由式(10)可得
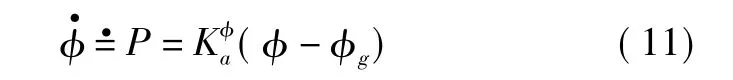
即
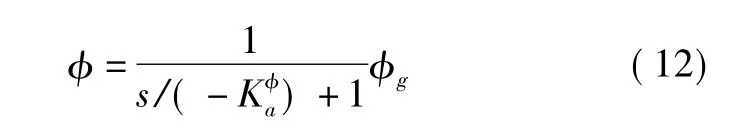

图5 滚转角控制器阶跃响应Fig.5 Step response of roll angle controller

图6 滚转角控制器伯德图Fig.6 Bode diagram of roll angle controller
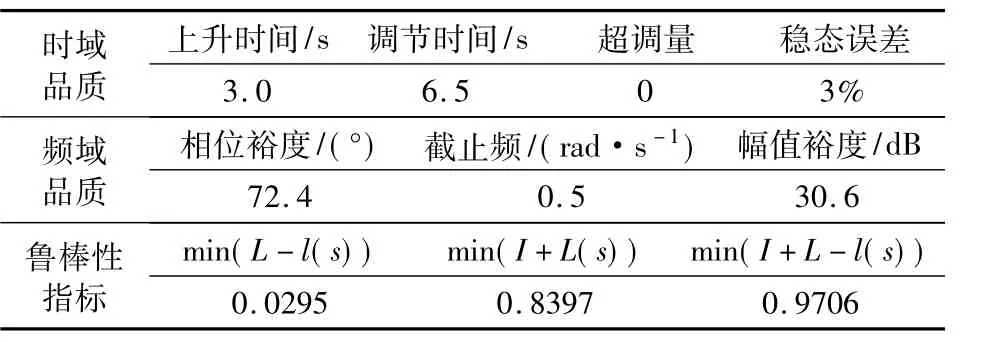
表1 滚转角控制器时频域控制品质Table 1 Control quality of roll angle controller in time-frequency domain
表1中的min(I+L(s))和min(I+L-l(s))分别为回差矩阵奇异值的最小值、逆回差矩阵奇异值的最小值。min(I+L(s))和min(I+L-l(s))越大,表明系统越稳定。
由图5可知,这种滚转角控制器存在稳态误差,图6的低频段也说明了这一现象。这一现象的物理意义是:无人机按某一滚转角滚转时,滚转角变化率偏航角变化率根据动力学方程

3 制导律设计
无人机横侧向制导回路的目标是使无人机以足够的准确度保持或跟踪预定的飞行航迹。若无人机偏离给定航迹,制导装置将测出其偏差,并以一定的控制规律控制姿态内回路,使无人机回到给定的航迹。本文采用控制律的结构如图7所示,数学表达式为
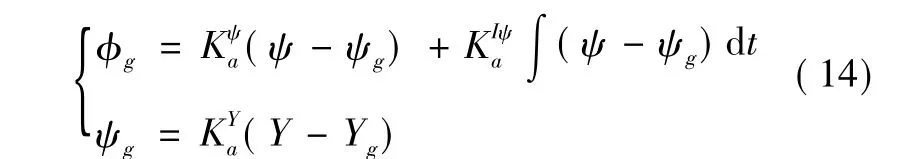
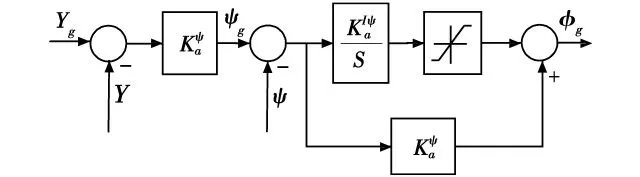
图7 航迹跟踪控制器结构示意图Fig.7 Structure diagram of path tracking controller
从飞机的横侧向动力学可知,飞机在横侧向的轨迹运动是基本没有阻尼的,如果仅采用侧偏的比例控制,势必形成轨迹运动的周期振荡,航迹角就是用来阻尼轨迹运动的,使轨迹运动形成良好的二阶环节特性,达到期望的轨迹控制指标。引入航迹角积分来消除系统的稳态误差。这种控制器结构在滚转角等存在测量误差时,可以无误差地跟踪航迹。无人机协调转弯时满足

其中,ay为侧向加速度。当 φ≤20°时,tan φ≈φ,则

由航迹角的定义可得

由式(14)得
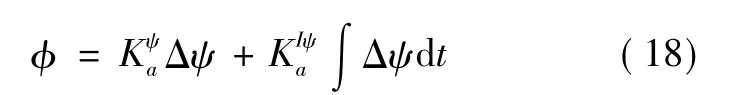
把式(16)、式(17)代入式(18)可得
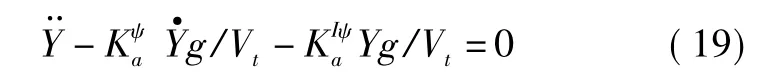
这是一个典型的二阶环节,写成
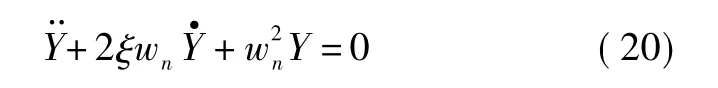
由式(14)得

即
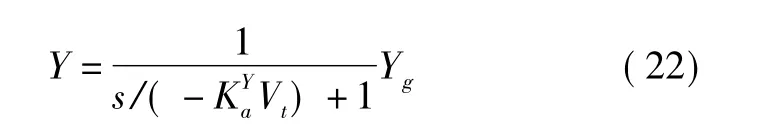
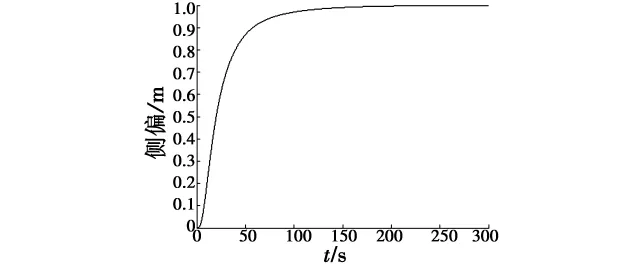
图8 航迹跟踪控制器阶跃响应Fig.8 Step response of path tracking controller
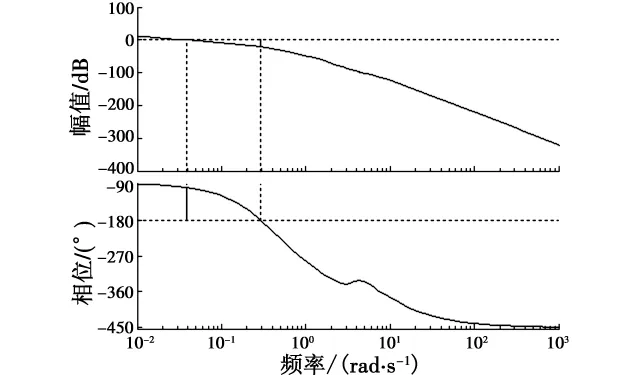
图9 航迹跟踪控制器伯德图Fig.9 Bode diagram of path tracking controller
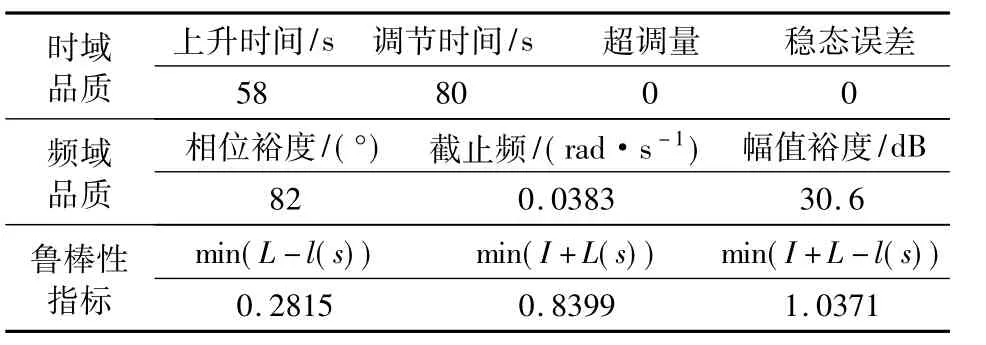
表2 航迹跟踪控制器时频域控制品质Table 2 Control quality of path tracking controller in time-frequency domain
4 仿真验证
选取样例无人机飞行状态为:海拔高度2000 m,速度40 m/s,迎角3.5°。在平飞状态下,分别在连续域和数字域下对样例无人机的滚转角控制器进行仿真,并与常规的滚转角控制器进行比较。常规滚转角控制器为
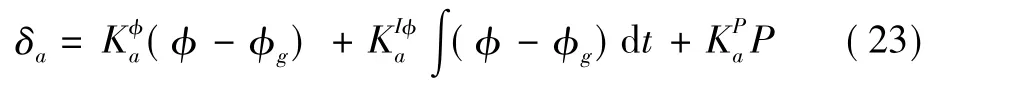
在连续域中给定滚转角为20°,两种滚转角控制器的响应曲线见图10,对应的滚转角速率的响应曲线如图11所示。
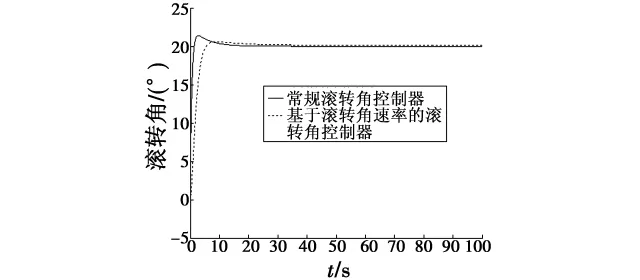
图10 滚转角响应曲线Fig.10 Response of roll angle controller
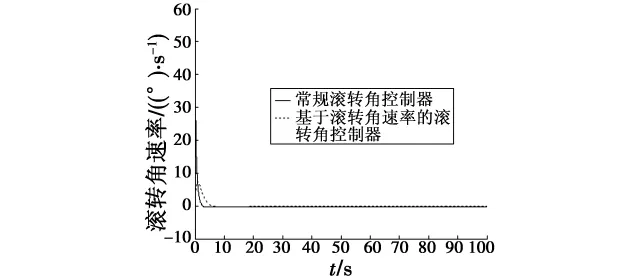
图11 滚转角速率响应曲线Fig.11 Response of roll rate controller
从图10和图11中可以看出,在连续域中,两种滚转角控制器都能满足控制要求。但常规的滚转角控制器在开始时有一个很大的滚转角速率冲击,这体现了样例无人机横侧向的特性,而用本文设计的基于滚转角速率的滚转角控制器就可以很好地抑制这种特性。由图10可以看出,本文设计的滚转角控制器的响应速度比常规滚转角控制器慢。对常规滚转角控制器而言,滚转角指令直接转化为舵面;而本文设计的滚转角控制器中,滚转角指令先转化为滚转角速率指令,通过滚转角速率的积分转化为舵面,这是一个相对较慢的过程,成功抑制了滚转角速率的变化速度,使得滚转角响应较平缓,超调很小。
现代无人机采用数字式飞行控制系统来完成各种飞行任务,对本文提出的滚转角控制律和式(23)控制律离散化后,仿真验证其控制品质。样例无人机控制律解算周期为20 ms、传感器采集频率为100 Hz。给定滚转角为20°,两种滚转角控制器的响应曲线见图12、图13,对应的滚转角速率的响应曲线如图14、图15所示。
由图12~图15可以看出,式(25)给出的基于滚转角的滚转角控制器在数字域中无法实现滚转角控制,对应的滚转角速率变化非常剧烈,而本文给出的基于滚转角速率的滚转角控制器的控制效果非常好,满足滚转角控制的要求。这种控制器在连续域中的调节时间为11 s,滚转角速率的最大值为5(°)/s;在数字域中的调节时间为10 s,滚转角速率的最大值为7.4(°)/s,该控制器在不同的环境中控制效果基本相同。
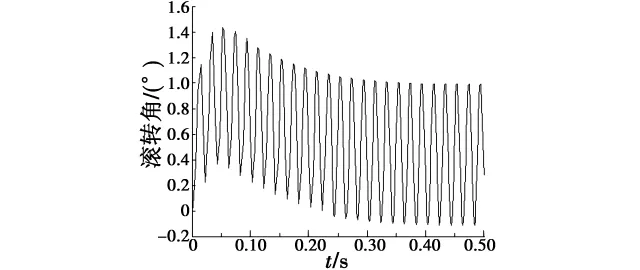
图12 常规滚转角控制器响应Fig.12 Response of conventional roll angle controller

图13 基于滚转角速率的滚转角控制器响应Fig.13 Response of roll angle controller based on roll rate
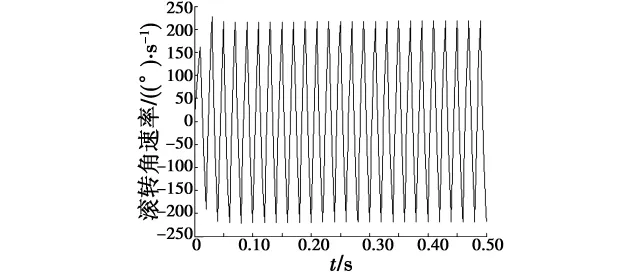
图14 常规滚转角控制器的滚转角速率响应Fig.14 Response of roll rate of conventional roll angle controller
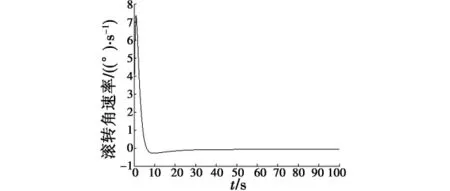
图15 本文中的滚转角控制器的滚转角速率响应Fig.15 Response of roll rate of roll angle controller in this paper
图16 、图17给出了常规滚转角控制器和本文设计的基于滚转角速率的滚转角控制器在连续域和离散域中的伯德图。
可以看出,离散化对系统稳定性的影响很小,可以忽略,这就说明了常规滚转角控制器在数字域中无法实现滚转角的控制不是系统离散化造成的。造成滚转角发散的主要原因是:在一个采样周期内,副翼保持为一定值,由于样例无人机绕X轴的转动惯量小、副翼效率高,会产生很大的滚转角速率,使得常规控制器中的成为主控项,进而无法实现滚转角的控制。而本文设计的滚转角控制器中的滚转角速率积分就可以抑制滚转角速率的快速变化。
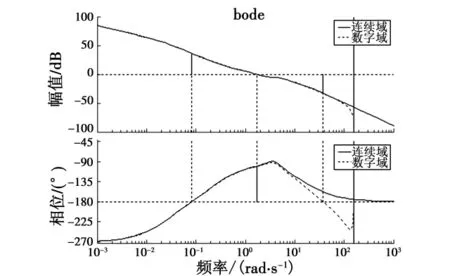
图16 常规滚转角控制器连续域与离散域伯德图Fig.16 Bode of conventional roll angle controller in s and z domain
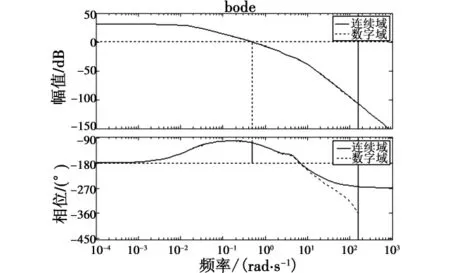
图17 本文中的滚转角控制器连续域与离散域伯德图Fig.17 Bode of roll controller based on roll rate in s and z domain
为了验证航迹跟踪控制器,本文在滚转角存在测量误差(2°)、样例无人机存在一个恒定的滚转力矩(100 N·m)和存在随机的滚转力矩(白噪声)的情况下对其进行仿真,如图18所示。
可以看出,这种航迹跟踪控制器在存在各种扰动的情况下,均可以实现无差的航迹跟踪。
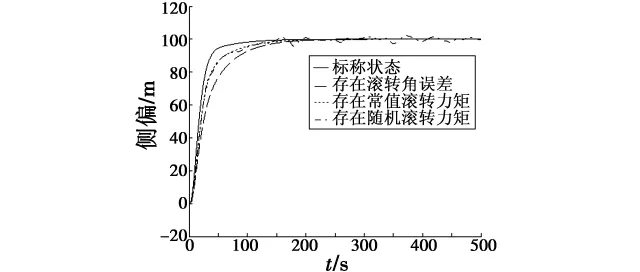
图18 基于滚转角速率的航迹跟踪控制器响应Fig.18 Response of path tracing controller based on roll rate
5 结束语
本文根据样例无人机的特点,给出了一种基于滚转角速率的横侧向控制方案,分别对姿态控制器和航迹跟踪控制器进行了研究,并与基于滚转角的姿态控制器进行比较。仿真结果表明,基于滚转角速率的控制器抗干扰能力强、鲁棒性好。
[1] WISE K A.Guidance and control for military systems:Future challenges[C]//AIAA-2007-6867,2007.
[2] SADRAEY M,COLGREN R.Tow DOF robust nonlinear autopilot design for a small UAV using a combination of dynamic inversion and H∞loop shaping[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit,15-18 August 2005,San Francisco,California,AIAA-2005-6402,2005.
[3] MATSUURA A,SUZUKI S.Lateral guidance control of UAV using feedback error learning[DB/OL].http://www.docin.com/p.205934369.html.2007.
[4] 吴森堂,费玉华.飞行控制系统[M].北京:北京航空航天大学出版社,2005:46-234.
[5] WISE K A,BRINKER J S.Linear quadratic flight control for ejection seats[J].Journal of Guidance,Control,and Dynamics,1996,19(1):15-22.
[6] WISE K A.A trade study on missile autopilot design using optimal control theory[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit,AIAA-2007-6673,2007.
[7] 吴受章.最优控制理论与应用[M].北京:机械工业出版社,2008.

