对新课程实施下分类讨论思想的再认识
罗树全
(黄骅市智美学校,河北 黄骅 061100)
对新课程实施下分类讨论思想的再认识
罗树全
(黄骅市智美学校,河北 黄骅 061100)
分类讨论是初中数学重要的数学思想方法之一。新课程实施下重新认识分类讨论思想,加强分类讨论思想在学生学习活动中的渗透,让学生获得数学知识、技能和活动经验的同时获得数学思想方法,发展学生的思维能力,更好地培养学生的创新意识和实践能力。
新课程;分类讨论;再认识
数学课程标准要求,“通过义务教育阶段的数学学习,学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验”。分类讨论作为最基本的数学思想方法之一,它既是一种重要的数学思想,又是一种重要的解题方法。在新课程实施中,教师根据学生的年龄特征、认知规律和知识积累,在遵循科学性前提下,采用逐级递进、螺旋上升的原则,向学生适时渗透分类讨论的数学思想,对于发展学生的思维能力,养成良好的数学思维习惯有着重要的意义。
一、什么是分类讨论思想
分类讨论是指当问题所给的对象不能进行统一研究时,需要对研究对象按某个标准进行分类,然后逐类讨论,最后综合各类结果得到整个问题的答案。像这种先分类再讨论,把问题“分而治之,各个击破”的解决问题的思想就是分类讨论思想。
二、分类讨论思想在新课程实施中的地位和作用
数学课程标准指出:“数学思想蕴涵在数学知识形成、发展和应用的过程中,是数学知识和方法在更高层次上的抽象与概括,如归纳、演绎、抽象、转化、分类、模型、数形结合、随机等。学生在积极参与教学活动的过程中,通过独立思考、合作交流,逐步积累数学活动经验、感悟数学思想”。分类讨论思想作为一种基本的数学思想,在学生基础知识的获得,基本技能的形成,数学素养的提高,思维能力的发展,创新意识和实践能力的培养方面占有非常重要的地位。按照数学课程标准的要求,在学生学习活动中,积极引导学生通过实践、思考、探索、交流等方式,让学生在获得知识、形成技能、发展思维的同时,借助数学知识的载体功能,将分类讨论思想向学生逐级渗透,螺旋上升,逐步积累,不断完善,对于培养学生思维的条理性、严谨性和完整性,养成缜密思考的良好品质,提高和发展学生的思维能力有着举足轻重的作用。
三、分类讨论的基本原则
分类讨论思想的核心是对问题进行合理分类,要做到合理分类,需遵循分类讨论的四个基本原则。
1.同一性原则
分类必须按确定的同一标准进行,不能同时使用几个不同的分类标准,否则会导致分类的混乱。
例如:

显然,以上对三角形分类时,既按边又按角同时使用了两个标准进行分类,造成了分类的混乱。
2.完备性原则
分类应当完整,即分类后子项的外延之和应等于母项的外延,而不能出现分类后母项外延的遗漏。
例如:若a为实数,则
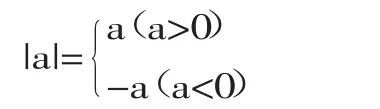
很明显,分类后丢掉了a=0的情况,造成分类后子项的外延出现了遗漏,导致分类不完整。
3.互斥性原则
分类后的每个子项都应当互不相容,相互排斥,不能出现分类后一些事物即属于这个子项又属于那个子项,造成子项外延的重叠。
例如:若a为实数,则
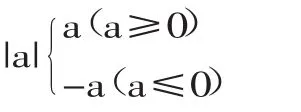
这里,分类后两个子项就出现了a=0在外延上的重叠,违背了子项外延互斥性原则。
4.逐级性原则
有些数学问题只需一次性分类,有些数学问题则需多次分类。多次分类是由于被讨论对象比较复杂,需把首次分类后的子项作为新的母项再进行分类,直至满足需要为止,进而达到解决整个问题的目的。
例如:求出方程(a-1)X+2X-6=0的实数根的情况。
解:当a-1=0即a=1时,方程为一元一次方程,其实数根为X=3

综上所述,
当a=1时,方程有唯一一个实数根。

四、分类讨论的一般步骤和结论归纳形式
分类讨论的一般步骤是:①确定分类讨论的对象及被讨论对象的全域。②确定分界点,统一分类标准,合理进行分类,并做到不重不漏,分层而不越级。③逐类讨论,分级进行。④综合归纳,得出结论。
分类讨论的结论归纳形式一般有三种:
①并列形式。格式为:当……时,有……;当……时,有……。
②并集形式。格式为:……或……。
③交集形式。格式为:……且……。
五、分类讨论的常见类型
引起分类讨论的因素较多,但常见的类型主要有以下几种:
①根据定义、性质、法则、公式、定理进行分类讨论。
②根据运算的要求进行分类讨论。
③根据图形的形状或位置变化进行分类讨论。
④当条件或结论开放时进行分类讨论。
⑤当问题中条件较少,需通过分类来补充条件时进行分类讨论。
六、学生在分类讨论中存在的问题
1.缺乏分类讨论的意识
例如:已知等腰三角形的两边长为8和6,求这个三角形的周长。
错解:等腰三角形的周长为8+8+6=22
分析:学生初解该类型题时,常因缺乏分类讨论的意识,仅考虑腰为8或腰为6中的某一种情况,而得出周长为22或20的单一性答案,造成问题丢解。
正解:当腰长为8时,等腰三角形周长为8+8+6=22
当腰长为6时,等腰三角形周长为6+6+8=20
所以,等腰三角形的周长是22或20。
2.存在盲目性
分类讨论的关键是确定分类标准,学生分类时常因不能准确找到分类标准的分界点,导致对问题盲目分类,出现求解上的失误。
例如:如图,一个等边三角形的边长和与它一边相切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直到回到原出发位置时,该圆自转了( )圈。
(A)2 (B)3 (C)4 (D)5
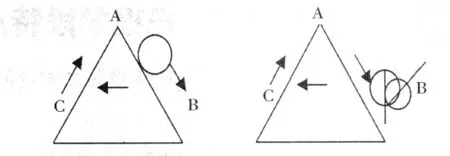
错解:选(B)
正解:选(C)
分析:因为圆与等边三角形相切且做无滑动旋转,很多学生盲目认为按圆在AB边、BC边、CA边上分类讨论即可,因为边长等于圆的周长,所以经过一条边刚好转了1圈,在三条边旋转当然转了3圈,故选(B)。然而却忽略了圆在顶点B、C、A处旋转的情况,由图(2)不难分析,圆经过一个顶点时旋转了120°,经过三个顶点共转了 120°×3=360°恰好为一圈,所以应选(C)。
3.存在主观臆断性
在分析数学问题时,一般当遇到数量的大小或符号不能确定以及图形位置或形状不确定时考虑分类讨论,但分类讨论绝不是凭主观臆断一开始就认为分类讨论,而是在计算或推理的过程中逢时而生,自然展开。
七、教师在新课程实施中渗透分类讨论思想的对策
在初中数学课程改革中,教师对分类讨论思想的渗透还存在一些不到位的地方,表现为:①在思想意识上,对分类讨论思想的重要性认识不足。②在教材运用上,对分类讨论思想挖掘不深。如对分类讨论思想在教材中的设置把脉不清,对分类讨论思想在教材中的层次缺少深度思考,对分类讨论思想的渗透缺乏整体规划与设计。③在教学过程上,对分类讨论思想渗透不强。教师往往关注知识的生成多,思想方法的渗透少;侧重就题论题多,思想方法的提炼少;注重知识系统多,思想方法的归纳少。④在实践应用上,对分类讨论思想提升不够。教师将分类讨论过多的停留在简单训练的层面上或训练模式的创新上,而忽视对思想方法的抽象与概括。那么,如何将分类讨论思想在新课程实施中有效地渗透呢?我觉得不妨从以下二个方面着手。
1.加强认识,明确目标要求
加强对数学课程标准的学习,充分挖掘教材中蕴藏的分类讨论思想,明确分类讨论思想在不同阶段的目标要求。数学课程标准把让学生获得适应社会生活和进一步发展所必需的数学思想方法作为教学的总体目标。人教版教材第一章【有理数】在学习了正负数后,以有理数的分类及绝对值的意义为载体最先拉开了分类讨论思想渗透的序幕。在以后的学习活动中,随着学习的深入,分类讨论思想由“隐性”向“显性”、由“方法”向“思想”逐步渗透,不断提升,最终实现由“思想”指导“方法”,达到水到渠成的功效。因此,教师在新课程实施中必须站在全局的高度统揽教学,对分类讨论思想的渗透既有整体规划和设计,又有明确而具体的目标和要求。
2.遵循原则,有效渗秀
在新课程实施中遵循逐级递进、螺旋上升的原则,将分类讨论思想有机渗透到每个阶段的教学之中。
(1)渗透“分类方法”,感知“分类思想”。由于初中生的数学知识比较贫乏,抽象思维能力较为薄弱,对数学思想方法还缺乏足够的了解,因此,在新课程实施中必须以知识的学习为载体,注重数学概念的生成过程、知识的发展过程和问题的解决过程,通过教师的启发引领,向学生逐步渗透“分类方法”,让学生在展开思维获取知识的同时初步感知分类思想。
(2)训练“分类方法”,领悟“分类思想”。教师在新课程实施中要充分挖掘教材中体现分类讨论思想方法的各种元素,根据学生年级的不同、知识的不同和认知能力的不同,对“分类方法”展开由浅入深、由易到难、由隐到显的层次性训练,使分类讨论思想在训练过程中多次孕育,不断领悟,初步形成。
(3)掌握“分类方法”,运用“分类思想”。学生对于“分类方法”的掌握,需经历一个学习、思考、训练、巩固的体验过程。同样,“分类思想”的形成也是在“分类方法”的渐进生成过程中逐步领悟、不断完善建立起来的。在新课程实施中,只有把分类方法提升到分类思想的高度加以认识,才能变知识的生成过程为数学思想方法的形成过程,从而把分类讨论思想进行有效迁移和灵活运用。
(4)提炼“分类方法”,完善“分类思想”。在学生自主探究学习中,教师要引导学生对分类讨论思想适时而恰当地进行提炼和概括,让分类讨论思想在概念教学中不断内化,在归纳总结中不断强化,在问题解决中不断深化。同时,教师还要锻炼学生对分类讨论思想进行自我提炼、自我揣摩和自我概括,使分类讨论思想不断提升和完善。
总之,在初中数学课程改革中,教师若只重视学生对知识的探究学习而忽视分类讨论思想的渗透,学生的知识水平就只能停留在肤浅的层面而难以提高;相反,教师若过于单纯地强调分类讨论思想而忽略对知识的探究学习,就会使教学变成无源之水,学生的学习也难以达到知识技能和思想方法的和谐统一协调发展,因此,在新课程实施中,教师不仅要注重学生数学知识的学习和技能的提高,更要重视揭示知识发生发展过程中所蕴含的数学思想方法。
张华伟)

