2012年三角函数命题热点展示

☉江苏省盐城市大冈中学 李 俊

从2012年全国及各省市高考试题看，对三角函数模块的考查没有根本的变化，仍是以考查“同角三角函数关系”“图像和性质”“三角恒等变换”“解三角形”为主，体现考试大纲要求的“稳中求变”的指导思想.下面以部分2012高考理科试题为例说明.

一、同角三角函数的关系

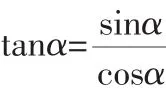
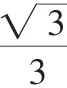
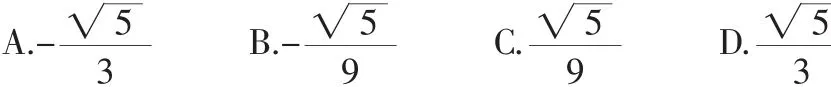
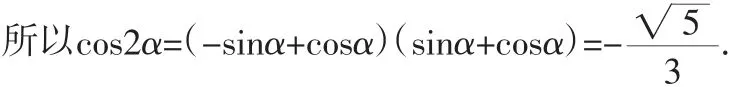
评析：本题主要考查三角函数中两角和差的公式以及二倍角公式的运用.首先利用平方关系得到二倍角的正弦值，然后利用二倍角余弦公式，将所求的转化为已知值.

二、三角函数的图像和性质

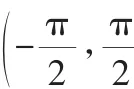
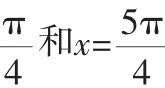
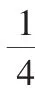
例3 （2012年浙江卷）把函数y＝cos2x＋1的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），然后向左平移1个单位长度，再向下平移1个单位长度，得到的图像是（ ）.

评析：主要考查三角函数的周期性、单调性、有界性、图像的平移等，以选择题、解答题为主，难度以容易题、中档题为主.

三、三角恒等变换

高考对此部分内容的考查，要求我们能从两角差的余弦公式，导出两角和与差的正弦、余弦、正切公式，二倍角的正弦、余弦、正切公式，了解它们的内在联系，公式之间的规律，能用上述的公式进行简单的恒等变换；注意三角恒等变换与其他知识的联系，如函数的周期性，三角函数与向量等内容.

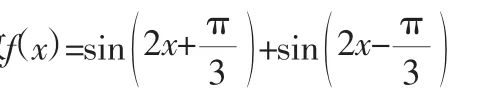
（1）求函数（fx）的最小正周期；

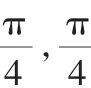
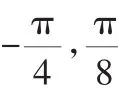
评析：本题主要考查两角和与差的正弦公式、二倍角的余弦公式，三角函数的最小正周期、单调性等基础知识，考查基本运算能力.难度不大，属中档题.

四、解三角形

高考对此部分内容的考查，要求我们掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题，能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的问题.解三角形时，要灵活运用已知条件，根据正、余弦定理，列出方程，进而求解，最后还要检验是否符合题意.

例5 （2012年全国新课标）已知a，b，c分别为△ABC三个内角A，B，C的对边，acosC

（1）求A；（2）若a=2，△ABC的面积为

解析：（1）由正弦定理得：

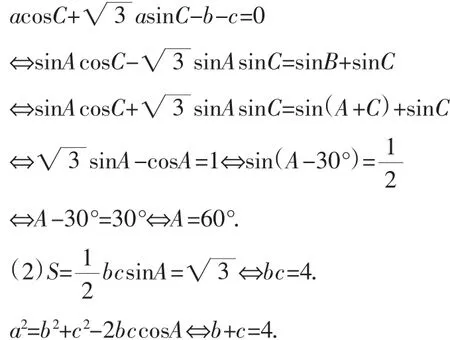
解得：b=c=2.

评析：本节是高考必考内容，重点为正、余弦定理及三角形面积公式，考题灵活多样，近几年经常以解答题的形式来考查，且常以解决实际问题为背景的试题形式出现.