不等式中的方案设计问题

☉湖北省孝感市文昌中学 罗小倩

近几年的中考数学中，经常出现以不等式为背景的方案设计问题.下面列举几例，供学习时参考.

1.购票的方案设计

例1 2008年8月，北京奥运会帆船比赛将在青岛国际帆船中心举行.观看帆船比赛的船票分为两种：A种船票600元/张，B种船票120元/张.某旅行社要为一个旅行团代购部分船票，在购票费不超过5000元的情况下，购买A，B两种船票共15张，要求A种船票的数量不少于B种船票数量的一半.若设购买A种船票x张，请你解答下列问题：

（1）共有几种符合题意的购票方案？写出解答过程.

（2）根据计算判断：哪种购票方案更省钱？

（2011年山东省青岛市）

解：（1）由题意：

因为x为整数，所以x＝5，6.

所以共两种购票方案：

方案一：A种船票5张，B种船票10张；

方案二：A种船票6张，B种船票9张.

（2）因为，第一种方案的票费为：5×600＋120×10＝4200（元）；

第二种方案的票费为：6×600＋120×9＝4680（元）；

所以，第一种方案更合算.

2.进货的方案设计

例2 某超市销售有甲、乙两种商品，甲商品每件进价10元，售价15元；乙商品每件进价30元，售价40元.

（1）若该超市同时一次购进甲、乙两种商品共80件，恰好用去1600元，求：能购进甲、乙两种商品各多少件？

（2）该超市为使甲、乙两种商品共80元的总利润（利润=售价-进价）不少于600元，但又不超过610元，请你帮助该超市设计相应的进货方案.

（2008年遵义市）

解：（1）甲商品进了x件，则乙种商品进了80-x件，依题意得：

10x+（80-x）×30=1600，解得：x=40.

即甲种商品进了40件，乙种商品进了80-40=40件.

（2）设购买甲种商品为x件，则购买乙种商品为（80-x）件，依题意可得：

600≤（15-10）x+（40-30）（80-x）≤610.

解得：38≤x≤40.

即有三种方案，分别为甲38件，乙42件或甲39件，乙41件或甲40件，乙40件.

3.租车的方案设计

例3 2008年5.12四川地震后，怀化市立即组织医护工作人员赶赴四川灾区参加伤员抢救工作.拟派30名医护人员，携带20件行李（药品、器械），租用甲、乙两种型号的汽车共8辆，日夜兼程赶赴灾区.经了解，甲种汽车每辆最多能载4人和3件行李，乙种汽车每辆最多能载2人和8件行李.

（1）设租用甲种汽车x辆，请你设计所有可能的租车方案；

（2）如果甲、乙两种汽车的租车费用每辆分别为8000元、6000元，请你选择最省钱的租车方案.

（2010年河南郑州市）

解：（1）因为租用甲种汽车为x辆，则租用乙种汽车（8-x）辆.

即共有两种租车方案：

第一种是租用甲种汽车7辆，乙种汽车1辆；

第二种是全部租用甲种汽车8辆.

（2）第一种租车方案的费用为7×8000+1×6000=62000（元）.

第二种租车方案的费用为8×8000=64000（元）.

所以，第一种租车方案最省钱.

例4 荣昌公司要将本公司100吨货物运往某地销售，经与春晨运输公司协商，计划租用甲、乙两种型号的汽车共6辆，用这6辆汽车一次将货物全部运走，其中每辆甲型汽车最多能装该种货物16吨，每辆乙型汽车最多能装该种货物18吨.已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元；租用2辆甲型汽车和1辆乙型汽车共需费用2450元，且同一种型号汽车每辆租车费用相同.

（1）求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元.

（2）若荣昌公司计划此次租车费用不超过5000元.通过计算求出该公司有几种租车方案？请你设计出来，并求出最低的租车费用.

（2008年黑龙江哈尔滨市）

解：（1）设租用一辆甲型汽车的费用是x元，租用一辆乙型汽车的费用是y元.

答：租用一辆甲型汽车的费用是800元，租用一辆乙型汽车的费用是850元.

（2）设租用甲型汽车z辆，则租用乙型汽车（6-z）辆.

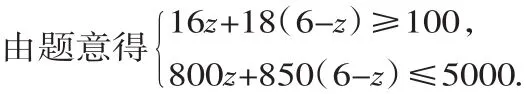
解得2≤z≤4.

由题意知，z为整数，则z=2或z=3或z=4.

故共有3种方案，分别是：

方案一：租用甲型汽车2辆，租用乙型汽车4辆；

方案二：租用甲型汽车3辆，租用乙型汽车3辆；

方案三：租用甲型汽车4辆，租用乙型汽车2辆.

方案一的费用是800×2+850×4=5000（元）；

方案二的费用是800×3+850×3=4950（元）；

方案三的费用是800×4+850×2=4900（元）.

所以最低运费是4900元.

答：共有3种方案，分别是：

方案一：租用甲型汽车2辆，租用乙型汽车4辆；

方案二：租用甲型汽车3辆，租用乙型汽车3辆；

方案三：租用甲型汽车4辆，租用乙型汽车2辆.

最低运费是4900元.

4.汽车调度的方案设计

例5 某物流公司，要将300吨物资运往某地，现有A、B两种型号的车可供调用，已知A型车每辆可装20吨，B型车每辆可装15吨，在每辆车不超载的条件下，把300吨物资装运完，问：在已确定调用5辆A型车的前提下至少还需调用B型车多少辆？

（2011年永州市）

解：设还需要B型车x辆，根据题意，得：

20×5+15x≥300.

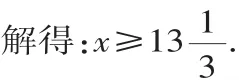
由于x是车的数量，应为整数，所以x的最小值为14.

答：至少需要14台B型车.