圆锥曲线动弦的“保值性”
☉江苏省灌云县杨集高级中学 李 昌
圆锥曲线的许多性质不仅优美而且和谐.文[1]得到了圆锥曲线中关于动弦的性质1.
性质1过圆锥曲线上一定点P任作两条动弦PA、PB,当这两弦的斜率之积、斜率之和或者倾斜角之和三者中有一个为定值时,动弦AB所在直线过定点或有定向.
此性质动静结合,很优美,但不具和谐性!因为条件中的动弦有两条,且它们在方向上存在某种静态,而结论中的动弦只有一条,其静态也不完全体现在方向上.由此想到:是否可以找到两条直线,它们的方向存在与条件相对应的静态呢?
结合性质1,进一步探究发现,动弦AB过定点Q时,直线PQ和曲线在点P处的切线l与动弦PA、PB在方向上具有一致的定值;动弦AB有定向时,动弦AB和曲线在点P处的切线l与动弦PA、PB在方向上也具有一致的定值.据此,既能使条件的定值在结论中得到保全,又能使定点定向归为统一,结论更优美和谐.故将其称为圆锥曲线动弦的“保值性”,即:
性质2过圆锥曲线上一定点P任作两条动弦PA、PB,设圆锥曲线C在点P处的切线为l,用kPA表示直线PA的斜率,αPA表示直线PA的倾斜角,其他类似.
(1)当kPA·kPB=t(t为定值)时,动弦AB所在直线若过定Q,在kPQ存在时,满足kPQ·kl=t,动弦AB若有定向,在kAB存在时,满足kAB·kl=t;
(2)当kPA+kPB=t(t为定值)时,动弦AB所在直线若过定Q,在kPQ存在时,满足kPQ+kl=t,动弦AB若有定向,在kAB存在时,满足kAB+kl=t;
(3)当αPA+αPB=α(α为定值)时,动弦AB所在直线若过定Q,则αPQ+αl=α,若有定向,则αAB+αl=α.
下面利用文[1]的结论以抛物线和椭圆为例进行证明,双曲线中的证明类似.
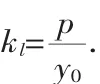

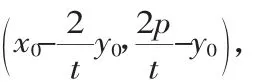






1.朱其录,申后坤.圆锥曲线动弦的一个性质.数学通报,2002,11.

