分段函数的求解策略

☉江苏省丹阳市珥陵高级中学 余学锋

分段函数的求解策略

☉江苏省丹阳市珥陵高级中学 余学锋

分段函数是指自变量在两个或两个以上不同的范围内，有不同的对应法则的函数.它是一个函数，却又常常被同学们误认为是几个函数.分段函数在高中数学中占有重要的位置，在高考试卷中也常常出现.为此，本文从如下几个方面进行系统的介绍.

1.求分段函数的定义域和值域

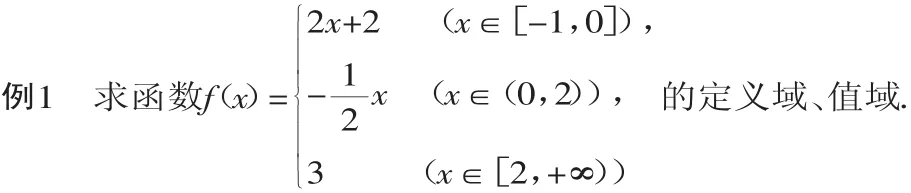
解：作图1，分段作图如下：

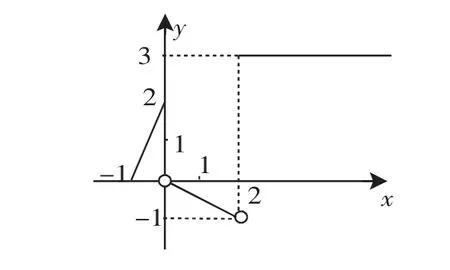
图1

利用“数形结合”，易知f（x）的定义域为［-1，+∞），值域为（-1，2］∪{3}.

点评：分段函数的定义域为每一段函数定义域的并集，在表示每一段函数中x的取值范围时，要确保做到定义域不重不漏，即交集为空集，并集为整个定义域.值域应是其定义域内不同子集上各关系式的取值范围的并集.

2.求分段函数的函数值

点评：利用分段函数的定义求值.

3.求分段函数的最值

易得该函数的最小值是3，则m≤3，即m的取值范围是（-∞，3］.

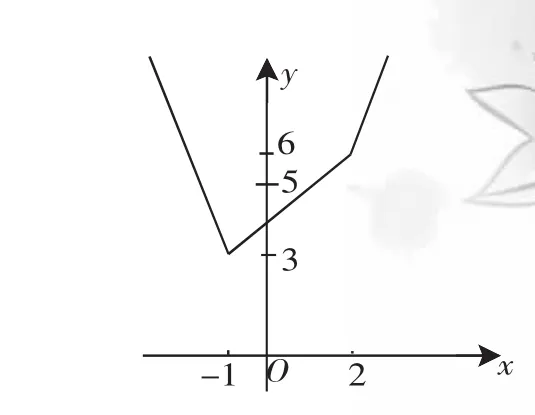
图2

点评：对型如m≥f（x）、n≤f（x）的恒成立问题，只须m≥f（x）max、n≤f（x）min即可.

4.判断分段函数的奇偶性

例4 （2006年上海春）已知函数f（x）是定义在（-∞，+∞）上的偶函数.当x∈（-∞，0） 时，f（x）=x-x4，则当x∈（0，+∞）时，f（x）=__________.

5.判断分段函数的单调性

点评：解决分段函数的单调性问题的策略是借助其图像，还需考虑分界点左右两侧函数值的大小.

6.解分段函数的方程

点评：分段求解，应注意所得方程的解是否在所给对应关系的范围内！