相交圆内一类内接蝶形的等积性质

☉福建省大田第一中学 田富德 吴赛瑛

相交圆内一类内接蝶形的等积性质

☉福建省大田第一中学 田富德 吴赛瑛

笔者对相交圆内接蝶形进行探究时，得到了两个有趣的等积性质.

为了陈述方便，先给出如下定义：

定义 两圆相交，若一个圆的圆弧含于另一个圆内，则称此段圆弧为该圆的内弧；若一个圆的圆弧不含于另一个圆内，则称此段圆弧为 该圆的外弧.其中内 弧和外弧均不包含两圆交点.如图1所示为圆O2的内弧为圆O1的外弧.

现以定理形式，将等积性质陈述如下：

定理1 圆O1与圆O2相交于A、B两点，过A的直线分别交圆O1与圆O2于F、E，过B的直线分别交圆O1与圆O2于D、C，若线段CD和线段EF不相交，CF交DE于M，则S△CDM=S△EFM.

证明：易知C、D至多一点在内弧，E、F至多一点在内弧.

（1）若C、D、E、F均在外弧上，如图1所示，连接CE、AB、DF.

因为A、B、D、F四点均在圆O1上，所以∠AFD=∠ABC.

因为A、B、C、E四点均在圆O2上，所以∠ABC+∠AEC=180°.

因此，∠AFD+∠AEC=180°，从而DF∥CE.

故S△CEF=S△CED，即S△CDM=S△EFM.

（2）若C、F在内弧上，D、E在外弧上，如图2所示.

连接AB、DF、CE.

因为A、D、B、F四点均在圆O1上，所以∠AFD=∠ABD.

因为A、C、B、E四点均在圆O2上，所以∠ABC=∠AEC.

因此∠AFD=∠ABD=∠ABC=∠AEC，从而DF∥CE.

故S△CEF=S△CED，即S△CDM=S△EFM.

若D、E在内弧上，C、F在外弧上，同上可证S△CDM=S△EFM.

（3）若D、F在内弧上，C、E在外弧上，如图3所示.

连接AB、DF、CE.

因为A、B、F、D四点均在圆O1上，所以∠BDF=∠BAF.

因为A、B、E、C四点均在圆O2上，所以∠BAE=∠BCE.

因此∠BDF=∠BAF=∠BAE=∠BCE，从而DF//CE.

故S△CEF=S△CED，即S△CDM=S△EFM.

若C、E在内弧上，D、F在外弧上，同上可证S△CDM=S△EFM.

（4）若F在内弧上，C、D、E在外弧上，如图4所示.

连接AB、DF、CE.

因为A、F、B、D四点均在圆O1上，所以∠AFD=∠ABD.

因为A、B、C、E四点均在圆O2上，所以∠ABD=∠AEC.

因此，∠AFD=∠AEC，从而DF∥CE.

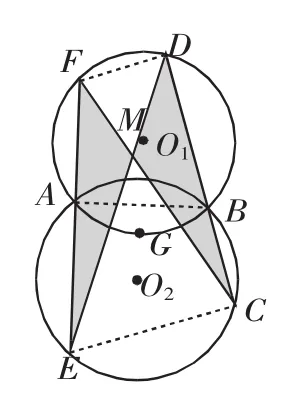
图1

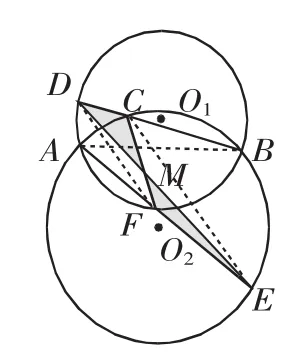
图2

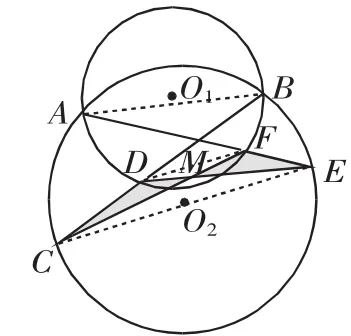
图3

图4

故S△CEF=S△CED，即S△CDM=S△EFM.

若C、D、E、F其中一点在内弧，另三点在外弧，同上可证S△CDM=S△EFM.

综上，定理1得证.

定理2 圆O1与圆O2相交于A、B两点，过A的直线分别交圆O1与圆O2于F、E，过B的直线分别交圆O1与圆O2于D、C，若线段CD和线段EF相交于M，连接CF、DE，则S△CFM=S△EDM.

证明：易知C、D至多一点在内弧，E、F至多一点在内弧.

（1）若C、D、E、F均在外弧上，如图5所示.

连接AB、CE、DF、AC、BE.

因为A、B、D、F四点均在圆O1上，所以∠AFD=∠ABC.

因为A、B、E、C四点均在圆O2上，

所以∠CAE=∠CBE及∠ABE+∠ACE=180°.

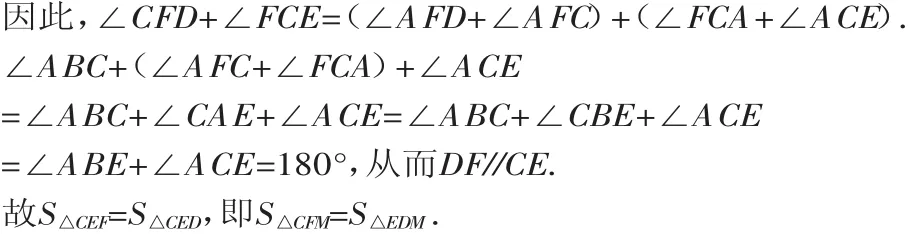
（2）若D、F在内弧上，C、E在外弧上，如图6所示，

连接AB、DF、CE、AC、BE.

因为A、B、E、C四点均在圆O1上，

所以∠CAE=∠CBE及∠ACE+∠ABE=180°.

因为A、B、D、F四点均在圆O2上，所以∠EFD=∠ABD.

因此，∠CFD+∠FCE=（∠CFE+∠EFD）+∠FCE

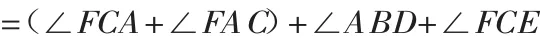
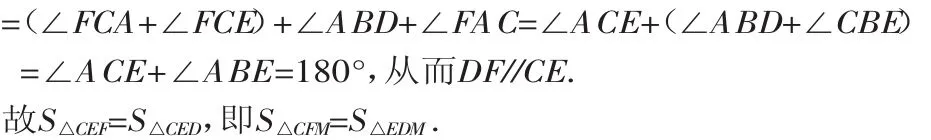
若C、E在内弧上，D、F在外弧上，同上可证S△CFM=S△EDM.

若C、F在内弧上，D、E在外弧上，线段CD和线段EF不相交，与条件矛盾.

若D、E在内弧上，C、F在外弧上，线段CD和线段EF也不相交，与条件矛盾.

（3）若F在内弧上，C、D、E在外弧上，如图7所示.

连接AB、DF、CE.

因为A、F、B、D四点均在圆O1上，所以∠BAF=∠BDF.

因为A、B、E、C四点均在圆O2上，所以∠BAE=∠BCE.

∠DCE=∠BCE=∠BAE=∠BAF=∠BDF=∠CDF，因此，∠ECF+∠CFD=（∠DCE+∠FCD）+∠CFD=∠CDF+∠FCD+∠CFD=180°（三角形内角和定理），从而DF∥CE.

故S△CEF=S△CED，即S△CDM=S△EFM.

若C、D、E、F其中一点在内弧，另三点在外弧，同上可证S△CDM=S△EFM.

综上，定理2得证.

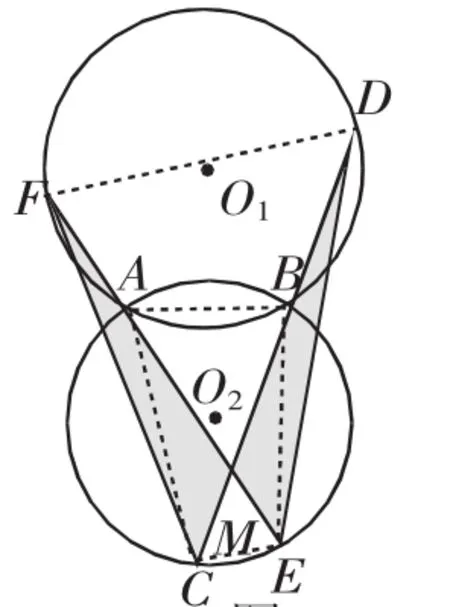
图5

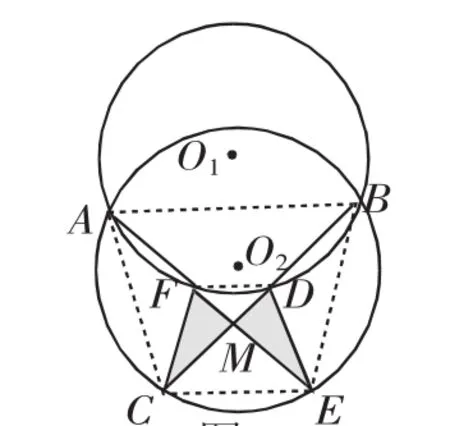
图6

图7