浅析2011年高考题中几何图形变化

☉江苏省宝应县范水高级中学 刘 峰 袁先军

浅析2011年高考题中几何图形变化

☉江苏省宝应县范水高级中学 刘 峰 袁先军

纵观2011年全国各省市高考题，考查几何图形位置的变化，由传统的图形翻折，发展到图形的平移、剪折、滚动等.现举例说明如下.

一、翻折

（1）当棱锥A′-PBCD的体积最大时，求PA的长；

（2）若点P为AB的中点，E为A′C的中点，求证：A′B⊥DE.

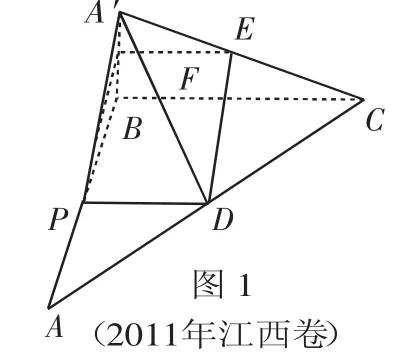
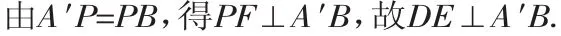
评注：本题考查了空间几何体的体积及空间中的位置关系等知识，将导数与函数思想融于立体几何题目中，解题时需具备一定的运算能力.

二、平移

例2 如图2所示的几何体是将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右水平平移后得到的，A、A′、B、B′分别为弧CD、C′D′、DE、D′E′的中点，O1、O1′、O2、O2′分别为CD、C′D′、DE、D′E′的中点.

（1）证明：O1′、A′、O2′、B四点共面；

（2）设G为AA′的中点，延长A′O1′到H′，使O1′H′=A′O1′，证明：BO2′⊥平面H′B′G.

证明：（1）由题意知A′、O1′、B′、O2′四点共面.

由O1′、O2′分别为C′D′、D′E′的中点，A′、B′分别为弧C′D′、D′E′的中点，得O1′A′∥B′O2′.

O2、B分别为DE、弧DE的中点，连接BO2，则BO2∥B′O2′，可知O1′A′∥BO2，所以O1′、A′、O2′、B四点共面.

（2）连接AO1，并延长至H，使得O1H=AO1，连接H′H、HB、O2O2′、O1O1′、HO1′，则得长方体HBO2O1-H′B′O2′O1′，所以HO1′∥BO2′，H′B′⊥BO2′.

评注：本题考查直圆柱的结构特征，圆的相关知识，空间中线面垂直的证明等知识，同时还考查空间想象能力，推理论证能力，运算求解能力等.

三、剪折

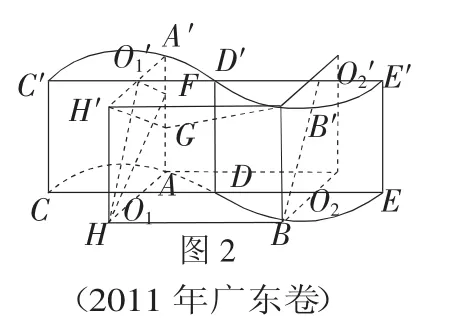
例3 请你设计一个包装盒，如图3所示，四边形ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A、B、C、D四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒.E、F在AB上，是被切去的一个等腰直角三角形斜边的两个端点，设AE=FB=x（cm）.

（1）某广告商要求包装盒的侧面积S（cm2）最大，试问x应取何值？

（2）某厂商要求包装盒的容积V（cm3）最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值.

解：设包装盒的高为hcm，底面边长为acm

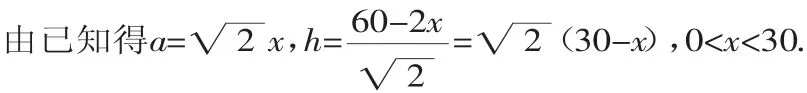
（1）S=4ah=8x（30-x）=-8（x-15）2+1800，所以当x=15时，S取得最大值.

评注：本题考查数学建模、二次函数的性质和最值、导数与函数的单调性、最值的关系，考查运用数学知识解决实际问题的能力.