平面电磁波在多分层介质中的传播特性研究

王龙波 赵 睿

（1.西北工业大学附属中学 陕西 西安 710068；2.西安市第一中学 陕西 西安 710082）

0 引言

电磁波为电磁振荡在介质中的传播，广义的电磁波包括无线电波，微波，红外线，可见光，紫外线，伦琴射线（X射线），伽玛射线。电磁波技术在通讯、遥控、制导、探测等诸多领域得到广泛应用。研究电磁波在介质中的传播问题，不仅对电磁场理论本身具有重要的理论意义，而且在实际应用中具有广泛的参考价值。电磁波在两种介质分界面的反射与透射是描述电磁波传播过程中的两个重要参数。对于电磁波在两种均匀介质和单个分界面下的反射与透射，根据麦克斯韦方程组及边界条件，理论已经比较成熟。随着电磁波在多层介质中传播的研究，还面临许多问题需要进行深入研究。

组成地球的物质性质变化是逐层变化的，因此我们认为地球具有分层结构[1]。特别在进行地下物质和目标探测时，需要考虑处在多层介质中被探测的目标，所以必须研究电磁波在多分层介质中的反射和透射问题。电磁波在多层介质中的传播问题，实质上都是解决电磁场在边界上的折射和反射问题[2]。本文将从分层介质中平面电磁波的传播和散射的问题，对多层或单层介质应用电磁场在边界上的条件，在介质中的传播，再到边界等等，直到最后一层的界面上折射及反射，以求出分层介质的反射系数和透射系数。在电磁波斜入射时，我们以波阻抗法求出了各层介质中反射系数和透射系数的理论计算公式。

1 平面电磁波在两种介质分界的反射和折射

考虑两种介质，平面电磁波入射到交界面上，则在两种介质中存在有如下三个电磁波：入射波，反射波和折射波。根据电磁场理论，可以求出垂直极化波的反射系数和投射系数：

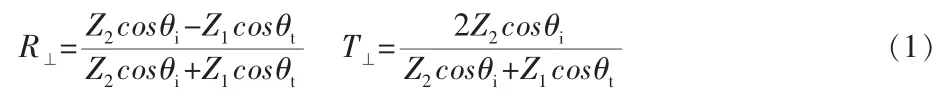
同理可以求出平行极化波的反射系数和投射系数：

当入射角θi→0时，上述情况变为正投射，当时，由（1），和（2）式可知 R//=R⊥→-1，T//=T⊥→0，这就表明入射波全部被反射，且反射波同入射波大小相等，但是相位恰好相反，也就是向边界上斜滑投射时，各种极性的平面波的反射系数均为-1。因此当我们十分倾斜的观察物体表面时，由于各种极化方向的反射光波的相位相同，彼此相加，使得物体显得比较明亮。

2 多层介质中平面电磁波的反射和透射

当平面电磁波入射多层介质时，除了入射区域和透射区域外，共n层介质和n+1个分界面。当一列平面电磁波垂直于介质边界入射时，实验表明反射波和透射波的性质与入射波的极化特性没有关系。因此，这时无法区分垂直极化和平行极化，但是理论表明，垂直极化和平行极化对反射和折射系数没有影响[3]。本文为简单起见，只讨论介质均由双轴介质组成，且各层介质的主光轴方向与我们所建立坐标轴的两个相互垂直的方向一致的情况。

电磁波在x，y，z方向的分量为：

设z方向波阻抗Zm：

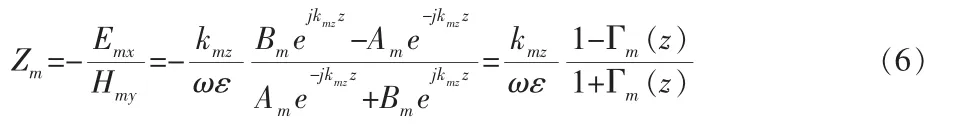
设特征阻抗zm=km/ωε，我们知道波阻抗在介质分界面的两侧是渐变的和连续的，根据以前计算可得特征阻抗与波阻抗的关系为[4-5]：

最后可得反射系数：

用am表示层m=1，2，…，n的上界面坐标，则有：

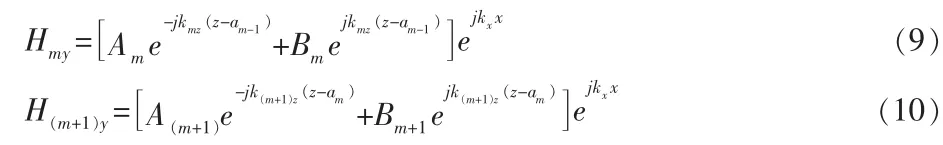
由边界条件可知在界面两侧应有Hy，Ex以及波阻抗连续[8]，则有：

将式（9），式（10）代入式（8）得：

将式（11），式（12）代入上式得：

由此可得到透射系数τ：

由此可递推出各层透射系数如下：

可以看到，电磁波斜入射的情况下，利用光学的反射和折射公式极方便。但是，在平面波对平面边界垂直人射的情下，例如在传输线、波导及某些自由波的情形，波阻抗方法的概念提供了更便捷的方法。

3 结语

本文从电磁场理论出发，推导了电磁波在多层层状介质中传播过程中，反射和透射与电磁波入射电磁波三者之间振幅的基本关系式，在此基础上，导出了各层介质的反射系数和透射系数的理论公式。从这些关系式可以了解每一层面的反射和透射情况。虽然在本文的分析过程中并没有考虑介质的损耗特性，但是从我们的讨论结果可以看出，如果考虑介质是有损耗的，我们讨论的结论仍然是成立的，只是相应的波阻抗变为复数，此时介质分界面的反射系数和透射系数也变为复数。说明反射波和透射波不是同相位了，两者之间有一定的相位移动。

［1］周学松.地下目标无损探测技术[M].北京：国防工业出版社，2005：40-41.

［2］陈军.现代光学及技术：电磁篇[M].杭州：浙江大学出版社，1996：56-59.

［3］曾昭发.探地雷达方法原理及应用[M].北京：科学出版社，2006：56-58.

［4］马如慧，刘生春.多分层介质中平面电磁波的传播特性分析[J].现代电子技术，2008，15（19）：36-38.

［5］谢处方，饶克谨.电磁场与电磁波[M].2 版.北京：高等教育出版社，1996：87-95.