物理解题中的另类分解方法＊——以两道高考题为例

叶玉琴

（安庆市第二中学 安徽 安庆 246000）

运动的合成和分解是处理曲线运动的常用方法，也是一个非常重要的方法.如平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动，这是非常熟悉的常规分解方法.其实，也可以采用其他方式分解，比如，可以将所有的抛体运动分解为沿初速度方向以初速度运动的匀速直线运动和自由落体运动.像竖直上抛运动就可以分解为竖直向上的匀速直线运动和自由落体运动.特别地，还可以将速度零（或曰静止）分解为两个任一时刻大小相等、方向相反的两个直线运动.这样的另类分解可以速解某些常规解析法难以求解的问题.下面以两道高考题的求解说明此解法的巧妙.

1 将速度零（或曰静止）分解为v和－v情形

【例1】（2008年高考江苏卷第14题）在场强为B的水平匀强磁场中，一质量为m、带正电q的小球在O点静止释放，小球的运动曲线如图1所示.已知此曲线在最低点的曲率半径为该点到x轴距离的2倍，重力加速度为g.求：

图1

（1）小球运动到任意位置P（x，y）的速率v；

（2）小球在运动过程中第一次下降的最大距离ym；

（3）当在上述磁场中再加上一竖直向上场强为E（E＞）的匀强电场时，小球从O静止释放后获得的最大速率vm.

解析：略去高考卷提供的参考答案解析.对于本题的（2）、（3）问可如下解答.

（2）将小球在O点的零初速度分解为水平向右的速度v和水平向左的－v，且满足qvB＝mg.这样小球以水平向右的速度v运动时所受的洛伦兹力与所受的重力相平衡，于是就可以将小球的复杂运动分解成水平向右的匀速直线运动和以O点作为圆周最高点的逆时针方向的匀速圆周运动，如图2（a）所示.所以小球在运动过程中第一次下降的最大距离即为该圆周的直径，故

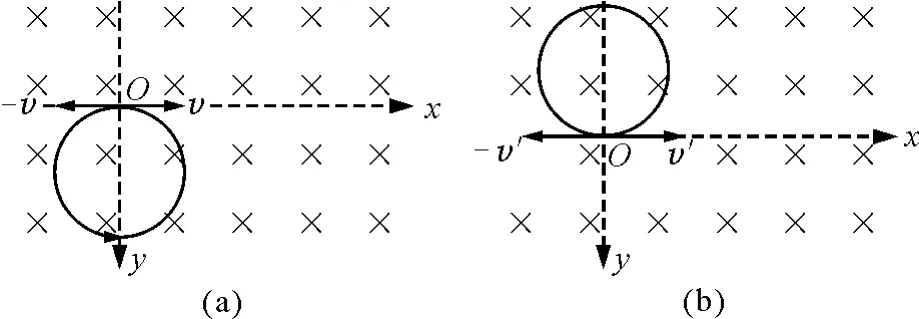
图2

（3）当再加上一竖直向上的场强为E（E＞）的匀强电场时，运用等效思想可将重力场和匀强电场合成为一等效场.其场力为（qE－mg），方向竖直向上；如法炮制，如图2（b）所示将小球在O点的初速度零分解为水平向右的速度v′和水平向左的速度－v′，且满足qv′B＝qE－mg.这样小球以水平向左的速度－v′运动时所受的洛伦兹力与所受的等效场力相平衡，于是就可以将小球的复杂运动分解成水平向左的匀速直线运动和以O点作为圆周最低点的逆时针方向的匀速圆周运动.所以当小球到达圆周的最高点时获得最大速率，故最大速率为

2 将不为零的速度v0分解为v1和v2情形

【例2】（2011年高考福建卷第22题）如图3（a），在x＞0的空间中存在沿y轴负方向的匀强电场和垂直于xOy平面向里的匀强磁场，电场强度大小为E，磁感应强度大小为B.一质量为m、带电荷量为q（q＞0）的粒子从坐标原点O处，以初速度v0沿x轴正方向射入，粒子的运动轨迹见图3（a），不计粒子的重力.

（1）求该粒子运动到y＝h时的速度大小v；

（2）现只改变入射粒子初速度的大小，发现初速度大小不同的粒子虽然运动轨迹（y-x曲线）不同，但具有相同的空间周期性，如图3（b）所示；同时，这些粒子在y轴方向上的运动（y-t关系）是简谐运动，且都具有相同的周期T＝.

1）求粒子在一个周期T内，沿x轴方向前进的距离；

2）当入射粒子的初速度大小为v0时，其y-t图像如图3（c）所示，求该粒子在y轴方向上做简谐运动的振幅A，并写出y（t）的表达式.

图3

解析：略去高考卷提供的参考答案解析.对于本题的（2）问可如下解答.

2）如图4所示，当入射粒子的初速度大小为v0时，该粒子的一个分运动是以O点作为起点同时又为圆周最低点的逆时针方向、速度大小为v2＝v0－v1的匀速圆周运动，圆周的半径r即为粒子在y轴方向上简谐运动的振幅A，故

于是简谐运动的y（t）的表达式为

图4

点评：带电粒子在匀强磁场和恒力场（匀强电场、重力场）组成的复合场中运动时，其所受的洛伦兹力大小和方向随时间而变化；若其运动是复杂的曲线运动，涉及力学、电磁学等多方面知识内容，综合性强，能力要求高，常规解析法难度高，学生难以掌握和解决.因此在处理该类问题时，通过以上两例所阐述的另类分解速度法，将带电问题和带电粒子的复杂曲线运动分解为匀速直线运动和匀速圆周运动，即可巧妙地解答该类问题.

1 薛金星，原野.2008年全国及各省市高考试题全解·理科综合卷.北京：人民教育出版社，2008

2 薛金星，任玉娟.2011年全国及各省市高考试题全解·理科综合卷.西安：陕西出版集团，陕西人民教育出版社，2011