物理解题中的递推方法

杨国平

（绍兴市第一中学 浙江 绍兴 312000）

当所研究的问题中涉及相关联的物体较多，并且相互之间的作用有一定规律时，可根据题目特点，从某次具体作用开始，运用归纳、递推方法，得到一般的表达式（通式）.用递推法解题的关键是导出相邻两次递推关系式.

1 多个研究对象的递推（归纳）

中学物理常涉及到的多体问题有：按一定规律放置的一系列物体（存在相互作用的物体称为连接体）、电学元件的网状连接……对于这类问题，只要找到相邻两物体之间力、电流、体积等的分配关系，最后通常能归纳出一个通式.

【例1】有12块质量分布均匀且相同的积木块，每块长度为L，横截面是边长为的正方形.将它们在水平面上一块叠一块地搭成“单孔桥”，接触面光滑.要使此桥具有最大的跨度（桥孔底边的宽度），试计算跨度与桥孔高度之比值.

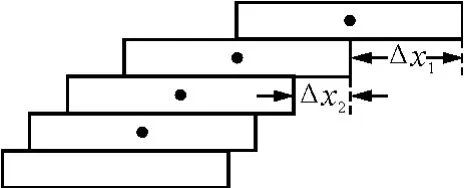
图1

设第2块（相对第3块）的最大伸出量为Δx2，每一积木块所受的重力均为G.对上面两木块，由力矩平衡可得

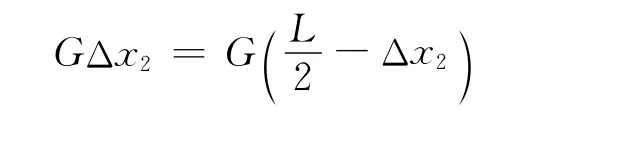
解得

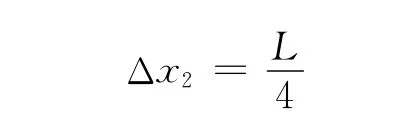
第3块最大伸出量Δx3满足

解得

依此类推，最后归纳得出

所以总跨度

跨度与桥孔高度之比值为

解析：把容器内剩余气体和抽气机里的气体看作一个整体，根据玻 －马定律，找出每抽气一次压强的变化规律，然后归纳递推出抽n次的压强表达式.

设初态时气体的压强为p0，容器的容积为V，抽气机的容积为ΔV.每抽一次气后压强分别为p1，p2，…，pn，则第1次抽气后

第2次抽气后

第3次抽气后

第n次抽气后

联立得

代入数据，得抽气的次数

2 多个过程的递推

最典型的情景莫过于多次碰撞，设法找出前后两次碰撞中遵循的规律，整个过程（的延续）往往归结为求等差数列或等比数列之和.这是数理结合的一个典范.

【例3】光滑水平面上固定一V字型槽，两边界与夹角α＝3°（图2中α被夸大了）.一小球从边的C点＝3m）以速度v＝3m／s、θ＝30°角的方向开始运动，与OA板发生碰撞后又折回与OB板碰撞 ……设所有碰撞都是弹性的.试求：

（1）小球经过几次碰撞后又回到C点；

（2）此过程所经历的时间.

图2

解析：小球在两板之间的碰撞类似于光的反射.

设小球第1次碰板时的夹角为θ1，如图3（a）所示，

第2次碰板时的夹角

第n次碰板时的夹角

当θn＝90°时小球将沿原路返回，代入数据，有

返回C点前共碰了39次.

（2）依次求出两次碰撞之间的时间，再累加，对本题并不有效，因为寻找两次运动时间的递推关系非常困难.可借助光的反射来突破.由镜像对称可知，光在两界面之间的多次反射可等效为镜面的多次成像，而光的传播方向不变.由图3（b）可知，入射点Cn就是离O最近的点，之后往返，总时间

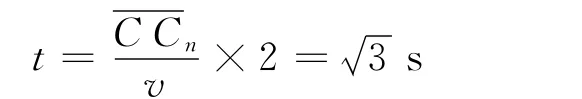
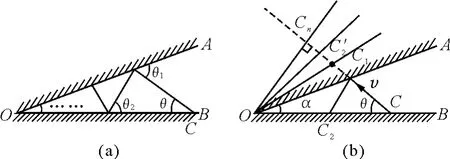
图3

【例4】一个导体A通过与另一带电导体B多次接触来充电，带电导体B的电荷在每一次接触后又都被充电到原来的值Q.假定A在第1次接触后带电荷量为q.试问采用这种方法A能达到的最大电荷量是多少［1］？

解析：导体接触必有电势相等，接触后带电荷量应分别与A，B的电容量成正比分配.即第1次接触后

设第2次接触后A带电荷量为q2，则

得

设第3次接触后A带电荷量为q3，则

得

依此类推，第n次接触后A所带电荷量qn应满足

依题意，当多次接触后A所带电荷量将达到最大值，即不再改变.故应有qn＝qn－1.则

即

解得

【例5】在一个开有小孔的原不带电的导体球壳中心O点，有一个点电荷Q，球壳内、外表面是同心球面，半径分别为a和b.欲将点电荷Q通过小孔缓慢地从O点移到无穷远，应当做多少功［2］.

解析：当点电荷在球心处，球内外表面分别感应产生等量异号电荷，感应电荷在球心处产生的电势为

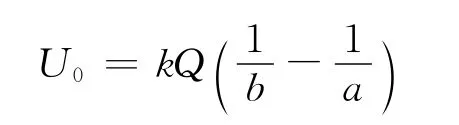
当点电荷Q从球心O点通过小孔移至无穷远处（电势为零）时，本题情况下，静电力做功不能写成

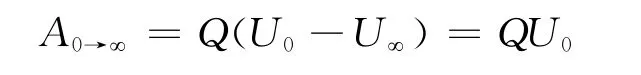
这是因为在移动Q时，O点电势必然变化，不能用不变的U0与电荷量Q的积QU0表示电场力的功.

那该怎么办呢？假设从O点通过小孔移出球壳外的电荷是一小份一小份地进行的.每移一小份电荷时，可以近似认为O点电势不变.再把移动每一小份电荷所做的功加起来，就是所求的总功.

设每次移动的电荷量为q（小量），Q＝nq，即n次移完（n很大）.逐次移q，外力做功分别为

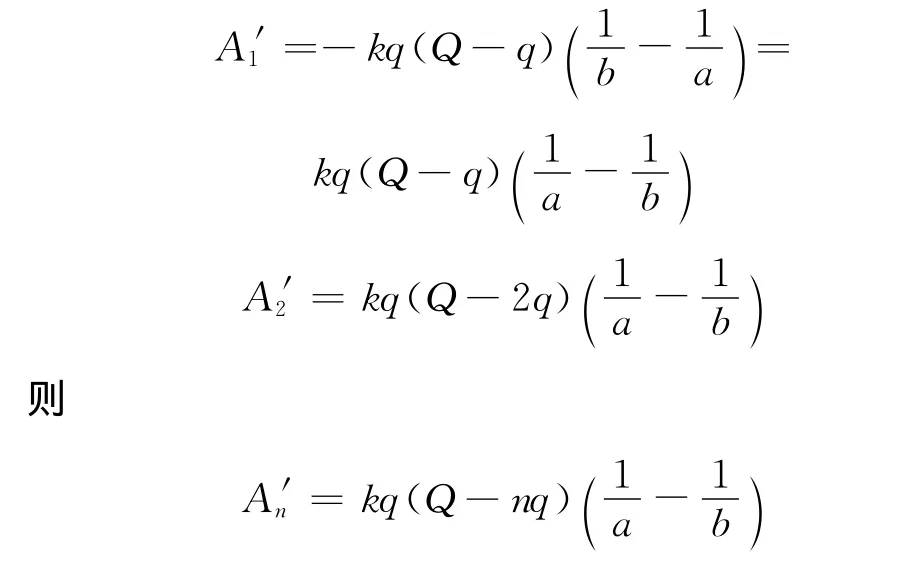
外力做的总功为

当q→0（即n→!）时，外力总功为

3 多物体多过程递推

物理问题大多来源于实际生活，对于竞赛题尤其如此.这样不可避免地要面对多个物体，以及多个运动过程.物理学科之难正在于此；然而，这也正是物理学科魅力之所在.

【例6】一块足够长的木板放在光滑水平面上，其上放有序号为1，2，3，…，n的相同小木块，如图4所示.小木块质量均为m，长木板质量等于小木块的总质量.给各小木块以相应的初速度v0，2v0，3v0，…，nv0，最终所有木块与长木板以共同速度匀速运动.求：

图4

（1）所有小木块与长木板一起匀速运动的速度vn；

（2）第1号小木块与长木板恰好相对静止时的速度v1；

（3）试推导第k号（k＜n）小木块与长木板相对静止时的速度.

解析：（1）由动量守恒知（小木块与板之间有摩擦）

解得

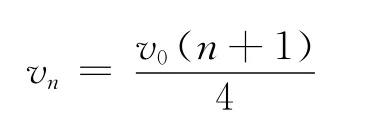
（2）各小木块做匀减速运动的加速度相同，在相同时间内的速度变化量相同，当1号木块与长木板的速度都为v1时，2号木块的速度为v1＋v0，3号木块的速度为v1＋2v0，依此类推，n号木块的速度为

据动量守恒定律有

解得

（3）同上，当2号木块与长木板的速度都为v2时，3号木块的速度为v2＋v0，4号木块的速度为v2＋2v0，依此类推，n号木块的速度为v2＋（n－2）v0，则有

当第k号同速时，有

4 警惕递推“陷阱”

根据题意列出递推关系式，再用数学归纳法或特殊数列求和等手段，是解决递推类问题的有效方法.但在某些情况下（尤其是涉及多个过程），不必按过程发生的先后顺序递推，而从初末状态的全程进行分析，可以起到奇效.在例3的求解过程中已露端倪.众所周知，对小车滑块系统，求多次来回后滑块在车上滑行的相对位移，最好采用能量守恒定律和摩擦生热的量度式，不要陷入递推陷阱中.事实上要避免这类陷阱并不容易，请看如下解答.

即得

例5方法2：做功的过程伴随着能量的转化（此处是静电场能）.初态时的等效电容量为

对应的静电场能

末状态电容器不再带电，电场能E2＝0，由功能关系，外力做功W＝ΔE，即得

1 谷明杰.高中物理解题思路16讲.天津：天津教育出版社 ，2006.7

2 范小辉.新编高中物理奥赛指导.南京：南京师范大学出版社，2005.417