路和圈的平方的Wiener指数
崔 康,叶永升
(淮北师范大学 数学科学学院,安徽 淮北235000)
1 引言
Wiener指数是应用于化学中一个经典的拓扑指数、Wiener是由Harold Wiener在1947年作为路径输入而引入的[1].Wiener指数倡导性地研究了饱和碳氢化合物与其结构性质之间的关系,根据碳原子之间的路径距离的计数,提出一个刻划分子结构的指数.Wiener指数等于碳氢化合物中所有最短碳-碳路径之和.分子的这一简单的数字表示已经被证实在定量结构关系(QSPR)中是一个非常有用的量[2-5].到目前为止,各国学者对Wiener指数进行了大量的研究并被最新应用于通讯网络等的研究中.
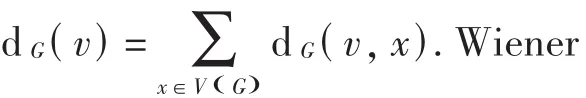
关于Wiener指数的研究已取得了很大进展,在文献[6]中已经研究了单圈图的Wiener指数,文献[7]中研究了路和圈联的Wiener指数.本文给出路和圈的平方的Wiener指数.
设 P是具有 n个顶点的路,连接图中所有距离为2的点所形成的图形、我们称之为路的平方 P2,其顶点集为 V= {v1,v2,…,vn},边集 E= {vlv2,vlv3,…,vn-2vn-1,vn-2vn,vn-1vn}.

证明对 k进行数学归纳法
(2)假设当 k=l-1时,结论是成立的,即

下面我们证明当 k=l时,结论是正确的.

同理,从顶点 v2l+1到其他顶点形成的顶点对之间距离之和是由归纳假可知,故对于 k=l.结论也成立.由(1)和(2)得:
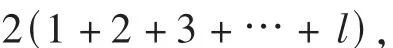

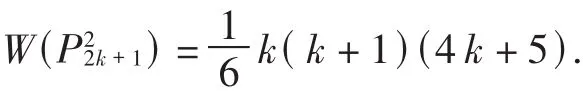
从而得出如下的定理.

3 圈的平方()的 Wiener指数
设 C是具有 n个顶点的圈,连接图中所有距离为2的点所形成的图形,我们称作圈的平方,记作.设Cn=vlv2v3… vnv1,则
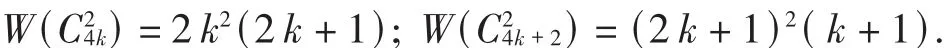
证明对 k进行数学归纳法.我们先证明 W()=2k2(2 k+1)是成立的.
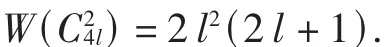
所以新增4点后相对于原图增加了

新增4点之后,原4 l个顶点形成的顶点对之间的距离也相应增加如下:顶点 v4l,v4l-1,v4l-2,…,v2l+4到顶点 vl距离增加了2,v2l+3到顶点 v1距离增加了1,即增加了2(2 l-2)+1;同理 v4l到点 v2,…,v2l+5,v2l+4,距离增加了2(2l-3)+1,以此类推,vl-l到 v3l+1的距离增加了2(2l-2l)+1共增加了
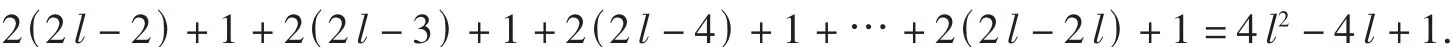
由归纳假设可知




证明我们首先证明 W(1)=k(k+1)(4k+1)是成立的
(2)假设当 k=l时,结论是成立的,即

原图增加一点后形成阶为4 l+1的新圈的平方的图,则顶点 v4l+1到点 v4l,v1以及 v4l-1,v2的距离是1;点v4l+1到点 v4l-2,v3以及 v4l-3,v4的距离均是2,依此类推 v4k+1到点 v2k-l,v2k+2以及 v2k,v2k+1的距离均是k,共增加了 4×1+4×2+… +4k,即 2l(l+1).
此外,除 v4l+1点外,图中所形成的顶点对之间距离也相应增加:v4l到 v2,v4,…,v2l-2形成的顶点对之间的距离增加了 l-1;v4l-l到 v3,v5,…,v2l-3形成的顶点对之间的距离增加了 l-2;依此类推,v2 l+6到v2l-4形成的顶点对之间的距离增加了1.然而与 v4l+1,…,v2l+6对称的这些点和对边也形成此等关系.故共增加了路径

由归纳假设可知

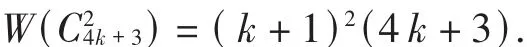
[1]WIENER H.Structural determination of paraffin boiling points[J].J Amer Chen Soc,1947,69:17-20.
[1]ROUVERAY D H.Predictinging chemistry from topology[J].Sci Amer,1986,255(9):40-47.
[3]DEVILLERS J.Topological indices and related descripotors in QSAR and QSPR[M].1999.
[4]GUTMAN I,POTGIETER J H.Wiener index and intermolecuhr forces[J].J Serb Chem Soc,1997,62:185-192.
[5]NIKOLIC'S,TRINAJSTI N C,MIHALI Z C.The Wiener index:developments and applications[J].Groat Chem Acta,1995,68:105-129.
[6]唐自凯.单圈图的Wiener指数[D].长沙:湖南师范大学,2006.
[7]余玲,叶永升.路和圈的联的Wiener指数[J].淮北师范大学学报:自然科学版,2011,32(1):1-3.

