交巡警服务平台设置与调度的数学模型
徐 标,陈 昊,杨文芳,鲁 群,张 硕
(淮北师范大学 数学科学学院,安徽 淮北 235000)
此问题为2011年全国大学生建模竞赛的B题第一部分,问题的背景见文[1],主要是结合重庆市交巡警服务平台设置的相关情况,建立数学模型分析研究下面的问题:
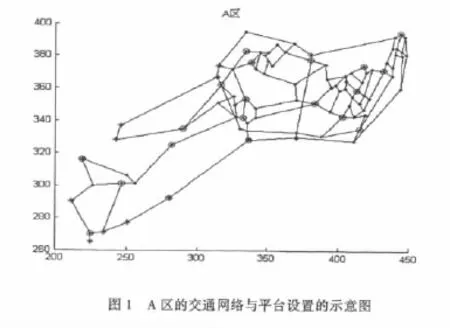
图1给出该市中心城区A的交通网络和现有的20个交巡警服务平台的设置情况示意图,相关的数据信息见文献[2].请为各交巡警服务平台分配管辖范围,使其在所管辖的范围内出现突发事件时,尽量能在3 min内有交巡警(警车的时速为60 km/h)到达事发地.
对于重大突发事件,需要调度全区20个交巡警服务平台的警力资源,对进出该区的13条交通要道实现快速全封锁.实际中一个平台的警力最多封锁一个路口,请给出该区交巡警服务平台警力合理的调度方案.
根据现有交巡警服务平台的工作量不均衡和有些地方出警时间过长的实际情况,拟在该区内再增加2-5个平台,请确定需要增加平台的具体个数和位置.
1 问题分析
首先利用Floyd[3]算法分别求出每个坐标节点到各平台 i(i=1,2,…,20)的最短距离,对各节点 j,选择使得距离 dij最小的路线.对于每个节点 j,将其划分到离它最近的平台管辖的区域,则得到一个初步的管辖范围,再对结果进行优化.
对于调度方案,本文采用最大时间最小化的方法[4-5],即选取到达每一个交通要道的时间最短的路线,而封锁的时间为选取的时间中最大的时间,再争取该最大时间最小,表示为max mindij,同时尽可能保证总时间最小.
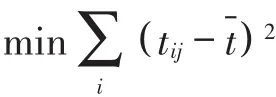
对现有方案进行研究时,首先从设立平台的原则考虑,将每个区域视为一个整体,将区域分为交通要道、重要部位两个部分,以重要部位的平均工作量代替区域的平均工作量,对交通要道、重要部位上的方案分别进行调整.其次从设立平台的任务来考虑,按层次分析法进行定性定量分析.综合分析结果,判断是否合理.
对于最佳围堵方案,为简化计算,假设嫌疑人逃跑后便设法在最短时间到达该市出口,则对于该市的13个出口存在13条最短路线.从而在全市内的围堵方案简化为对13条最短路线的围堵方案.
2 模型假设
假设1:警车在行驶过程中速度保持平稳;
假设2:每一个交巡警服务平台的警力资源足够应付其管辖区域的突发事件;
假设3:新增交巡警服务平台的财力资源足够;
假设4:由于嫌疑犯是驾车逃跑,所以假设嫌疑犯的逃跑速度与交巡警相同;
假设5:假设每个平台接到任务后马上出发,不考虑准备的时间.
3 模型的符号说明
X:路口节点的横坐标;Y:路口节点的纵坐标;v:警车行驶过程中的速度;tij:警车从服务平台 i到路口节点 j的时间;dij:警车从服务平台 i到路口节点 j的距离;sij:服务平台 i到达路口节点 j的路程;tmax:最大封锁时间;S:每个服务平台案发率的方差;X:每个服务台案发率的均值;t:增加平台以后的平均出警时间.
4 模型的建立与求解
4.1 A区交巡警服务平台的设置与调度
根据文献[2]给出的该市市中心城区A的交通网络和现有的20个交巡警服务平台的设置情况示意图,可以清楚地从图中了解各个服务平台的地理位置以及各个路口与服务平台的距离远近.要想设置服务平台或者要调度服务平台需先计算出每两个路口节点之间的距离,附件2[2]提供了每两个路口节点在图上的坐标值(X,Y),其中 X表示路口节点的横坐标,Y表示路口节点的纵坐标,再根据Floyd算法程序计算出A区内每两点之间的距离长度.由于地图的距离与实际的距离比是1:100 000,再将所算出的距离数值换算成实际的距离,从中挑选出符合题目要求的数据.
4.1.1 交巡警服务平台管辖范围的设置
4.1.1.1 模型的建立
将时间单位进行一致化处理,警车的速度为 v=60 km/h,即 v=103m/min,对于交巡警服务平台所管辖的范围内发生重大突发事件时,要在3 min内尽可能到达事发地点,就是要求服务平台与路口节点的实际距离不能超过3 000 m.
以时间 tij表示路口节点 i到服务平台 j的时间,根据附表中给出的各节点的坐标编写Floyd算法程序求出各节点之间的最小距离 dij(i=1,2,…,20;j=1,2,…,92),求得对应的时间 tij(i=1,2,…,20;j=1,2,…,92),表示为:

对于所写的程序,首先根据尽量小于3 min的原则对各节点间的时间矩阵进行筛选,将 tij大于3 min对应的路线剔除掉,对各节点 i,选择 tij最小的路线,其中 j为管辖节点的服务平台.
4.1.1.2 模型的求解
将上述模型中程序的运行结果进行优化.
存在的问题:第一,存在节点到各服务平台的最短行走时间均大于3 min,因此没有分配给任何服务平台管辖,如节点28,29,38,39,61,92.第二,由于平台周围节点的密集程度大不相同,所以存在管辖范围分配不均匀的情况,如节点1,20与节点10,14.
解决方案[6]:1)对于到每个平台的时间都超过3 min的节点,安排给离它最近的服务平台进行管辖.2)对于管辖范围严重不均衡的点,由于希望各平台总以最短时间到达事故现场,在允许行走时间最多增加10 s的前提下细微地做出一些调整.最终结果如表1和图2所示:

表1 各交巡警服务平台管辖范围

4.1.1.3 结果分析
上述结果表明,若发生紧急情况,可以保证有93.5%的节点能在3 min以内达到案发地点,因此该模型具有较高的可操作性.
但是平台的管辖区域并不均衡,这是因为各节点分布其本身已经存在着不均衡的情况,有些平台的设立除了自身区域外没有其他的管辖区域,则从节约资源的角度来看,可以将这些平台除去或者转移,结果会更优.
4.1.2 巡警服务平台警力合理的调度方案
4.1.2.1 模型的建立
由图1可以得知,A区有13条交通要道,对于产生的突发事件必须要在第一时间封锁交通要道,以尽快解决问题.A区总共有20个交巡警服务平台,且一个平台的警力最多封锁一个路口,合理安排这20个服务平台是必须的,每一个服务平台到交通要道的距离是不均衡的.封锁整个A区的时间是受最长时间制约,所以应当使最长时间最短,同时使总时间尽可能小.
4.1.2.2 模型的求解[7]
首先通过程序求出各平台到交通要道的最小时间,然后使用迭代的思想对结果进行优化,直至达到最优结果.具体求解过程如下:
(1)求出一组总时间最小的解.
(2)从这组解中取出时间最长的一个数据,对其进行优化,如果发生冲突就在一个数据确定的基础上求出一组新的解,如果没有冲突则继续进行第二步.
(3)直到对时间最长的数据进行优化时使总时间发生很大的增加,则停止优化,取当前解为最优解.
根据上文叙述的方法,通过计算.求出如下结果.

表2 各交通要道分管交巡警服务平台
通过线性规划:

求出一组更加优化的结果:

表3 各交通要道分管交巡警服务平台(优化)
4.1.2.3 结果分析
由求得结果的数据可以清楚地知道,每一个交巡警服务平台到达这13个交通要道的时间是不等的,有的甚至相差特别大,根据表3给出的数据可以分别找出到达13个交通要道的最短时间(不包括本身是要道的情况).

表4 平台到各要道的最小时间
由于要考虑这13个交通要道中的每一个要道都要被封锁,而且一个平台的警力最多封锁一个道路,因此不存在一个服务平台负责封锁两个交通要道的情况,则选取时间短的那条路线为准则,同时也要考虑这20个服务平台分别到达13个交通要道的最短时间,对比选取最优时间.根据这些条件的限制得出需要的交巡警服务平台的标号以及对应负责的交通要道标号及其需要的时间.

表5 最优方案
相比而言,最大封锁时间为:tmax=480.93 s=8.015 min.因此在8.015 min可以实现全封锁的目标.
4.1.3 服务平台的设置
4.1.3.1 模型的建立与求解
由上面所得出的结果以及原始数据可知,一些密集的地区处交巡警的工作量相对于其他地区交巡警的工作量大,也有一些地区的出警时间相对于其他服务平台的时间来得更长一些,因此需要增加一些服务平台来均衡工作量和优化出警时间.
在这里,由于要添加的服务平台数是未知的,但要满足如下条件:
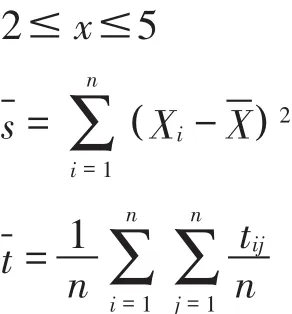
其中X为案发率的均值,Xi为每个服务平台的案发率,t为加 a个平台后的平均出警时间.
因为添加的服务平台的位置具有不确定性[8],将导致计算量很大.本文将采用枚举法的算法将交巡警服务平台需要的个数以及具体位置算出来,算法如下.
(1)在A区内,依次从2到5增加服务平台数 x.
(2)假设增加2个服务平台数,则依次编程求出每个服务平台案发率的方差及出警时间的长度.
(3)按照(2)式给定的方法分别对增加3个、4个、5个服务平台进行分析研究,从而得出最优的平台数和合理的安放位置,增加新的服务平台标号是:
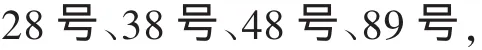
其方差为S=6.051 510;t=79.455 500 s.
4.1.3.2 结果的推广
如果该题不考虑设置服务平台数花费时间的话,也可以设置5个服务平台,相对于设置2个、3个、4个服务平台数要均衡些,设置的路口节点数以及对应的方差、出警时间如表6所示.

表6 增加5个服务平台的最优结果
表6中所显示的数据就是在一定的条件下,比如警力资源足够多,在允许建立足够多的服务平台数的情况下设置的优化方案.
[1]韩中庚,但琦.交巡警服务平台的设置与调度问题解析[J].数学建模及其应用,2012,1(1):67-72.
[2]全国大学生数学建模竞赛组委会 .2011 年竞赛 [EB/OL].[2011-09-10].http:∥www.mcm.edu.cn/html_cn/node/a1ffc4c5587c8a6f96eacefb8dbcc34e.html.
[3]林刘宁.运筹学[M].北京:北京邮电大学出版社,2003.
[4]孙霞林.用最优化选择原则求最短路径及长度[J].湖北师范学院学报,2002(2):72-74.
[5]孟凡江,高树喜,杨新安,等.多路径分配的车流径路优化模型[J].辽宁工程技术大学学报:自然科学版,2008,27(z1):93-95.
[6]郑畅.物流中心选址方法研究[M].武汉:武汉理工大学,2004.
[7]缪成.突发公共事件下应急物流中的优化运输问题的研究[D].上海:同济大学,2007.
[8]范丽芳,江浩斌,陈昆山.模糊层次分析法在配送中心选址中的应用[J].铁道货运,2005(11):20-23.

