菲涅尔数字全息成像研究

窦德召，汪徐德，姜恩华，周 正

(淮北师范大学 物理与电子信息学院，安徽 淮北 235000)

1967年Goodman等[1]提出利用光学方法产生全息图，采用电子技术、计算机技术来实现光学全息图的记录与再现的设想，这种技术被称为数字全息.1993年德国的Schnars和Jupnter真正实现全息图记录和再现的完全数字化[2].与传统的光学全息术相比较，数字全息术具有记录简单，可数值再现，可求解相位以及记录光谱范围广等优点，在物体形貌测量、显微成像、三维动态观测、光学相干断层成像、物体震动分析和无损检测等领域得到重要应用[3-6].成像理论、重建算法以及如何提高分辨率等方面一直是数字全息研究最关注的问题.本文主要通过实验对数字全息的成像特性进行较为详细的研究.

1 理论描述

1.1 菲涅尔数字全息图的记录

采用图1所示的光路记录透明物场的菲涅尔数字全息图.He-Ne激光器发出 λ=632.8 nm的激光束，经过平面反射镜 M1，反射后改变方向照射在分束镜 BS1上，并被分为两束:一束作为物光，先经过平面反射镜 M2反射，后经过小孔扩束镜 BE2扩束，由透镜 L2将其准直为平行光后照射到物体.另一束为参考光，扩束准直后经过平面反射镜 M3改变方向，再经分束镜 BS2反射，与物光在CCD光敏面板上相干叠加.P1和P2为衰减片，用来调节物光与参考光的光强比，从而使全息干涉条纹的对比度较好.

1.2 菲涅尔数字全息图的菲涅尔数值再现

菲涅尔数值再现方法是数字全息术中一种较广泛使用的再现方法.它是对光学再现过程的直接数值模拟.它引入数字重建光波，利用离散化的菲涅尔─基尔霍夫衍射公式模拟透射光波在菲涅尔域的传播，其再现结果和光学全息一样同时存在孪生像和直流项的干扰.接下来的讨论中采用如图2所示的坐标系.

图2 数字全息记录和重建坐标

式(1)为菲涅尔─基尔霍夫衍射公式，其中 r(x，y)为重建光波，I(x，y)为全息图光强分布函数.它重建了全息图后距离为 d的实像平面处的光波场，其强度为:

各点处的相位值是:

(1)式的离散形式为:

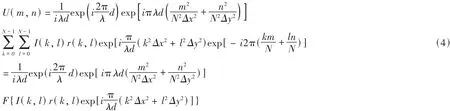
式中 F代表傅里叶变换，数值计算时多利用FFT快速傅立叶变换算法实现，可有效提高计算速度，最终求得像平面上光场的复振幅分布.

1.3 菲涅尔数字全息图的角谱数值算法再现

式中

是描述传播现象在频率域中的传递函数，当cos2α+cos2β＜1时，可对相位因子的开方式作二项式展开，在满足菲涅尔条件下，也就是在菲涅尔区域内式(6)可化简为:

将式(7)代入式(5)中可得:

由于

所以

式(8)可改写为:

式(8)和式(10)都是在频率域中表述的菲涅尔公式.利用式(8)或(10)在频域处理菲涅尔衍射问题会较为方便.

2 实验结果和分析

实验中采用图1所示光路记录透明物场的同轴菲涅尔数字全息图.所用物体为透射型光学分辨率测试板上的一组细线，共3根，每根宽度为80 μm.图3是拍摄到的全息图，图4是利用菲涅尔数值重建法得到的直接再现像，图5是对全息图用减均值法处理后的再现像.这些像都是经过放大后显示的.消除零级衍射像但未经放大直接显示的再现像则如图6所示，图像表明其有效像素较少，看不清楚.

可见，与光学全息一样数字同轴全息术的再现像仍然受到孪生像，直流项，互调制项的影响.表现为再现像面上各干扰项占据较大范围的灰度值分布，以致改变了要观察的再现像上的灰度分布且使其模糊不清.直接再现得到的图4其中间的正方形是直流项，而互调制项和孪生像表现为其中的一些模糊条纹.理想情况下应该从图4中观察到3根明锐的亮线，却因为上述干扰降低了像面上一些像素的灰度值，以致再现像呈黑白相间状.但是数字全息术由于采用的是数字再现方式，这就可以借助数字图像处理的方法对数字全息图进行预处理，从而改善再现像的像质.采用减均值法对全息图进行预处理，滤掉其直流项后得到如图5所示的再现像.由于在一定程度上抑制了直流项，再现像质得到显著改善.

图6 放大前的再现像

图7 角谱法再现像

图7是采用角谱算法在频率域中得到的再现像，同样采用了数字图像处理的方法消除了直流衍射像的影响，但与图5不同，图7并没有经过放大后显示，可见与采用菲涅尔数值算法从空域重建物场相比，采用角谱再现方法得到的再现像其有效像素较多，像质较好.

[1]GOODMAN J W，LAWRENCE R W.Digital image formation from electronically detected holograms[J].Appl Phys Lett，1967，1(3):77-79.

[2]SCHNARS U，JUPTNER W.Direct recording of holograms by a CCD target and numerical reconstruction[J].Appl Opt，1994，33(2):179-181.

[3]SCHNARS U，THOMAS K，JUMPTNER W.CCD-recording and numerical reconstruction of holograms and holographic interferograms[J].Pro of SPIE，1995，2 544:57-73.

[4]YU Lingfeng.Iterative algorithm with a constraint conditon for munerical reconstruction of a three-dimensional object from its hologram[J].J Opt Soc Am A，2001，18:1 033-1 045.

[5]KEBBEL V.Application of digital holographic microscopy for inspection of micro-optical components[J].Proc of SPIE，2001，4 398:189-198.

[6]SERGEY A.Spatially resolved Fourier holographic light scattering angular spectroscopy[J].Opt Lett， 2005，30(24):3 305-3 308.

[7]THOMAS K，JUPTNER W.Suppression of the dc term in digital holography[J].Opt Eng，1997，36(5):2 357-2 360.

[8]TAKANORI N，BAHRAM J.Object recognition by use of polarimetric phase-shifting digital holography[J].Opt Lett， 2007，32(15)，2 146-2 148.

[9]YAMAGUCHI，ZHANG T.Phase-shifting digital holography[J].Opt Lett，2009，34(16):1 268-1 270.