四元数分析中正则函数向量的非线性边值问题
鄢盛勇
(成都师范学院数学系,四川成都611130)
四元数分析、Clifford分析是近代分析的重要分支,它有非常重要的理论意义和应用价值,如在Maxwell方程、Yang-Mill场理论以及量子力学等方面都应用到它的结论[1-2].近年来许多学者研究了四元数分析中的一些奇异积分算子,并考虑了其中一些边值问题[3-4].文献[5]研究了 Clifford分析中无界域上正则函数向量的非线性边值问题.本文利用积分方程的方法和Schauder不动点定理,讨论四元数分析中有界域上正则函数向量适合下列边界条件的一类带共轭的非线性边值问题:
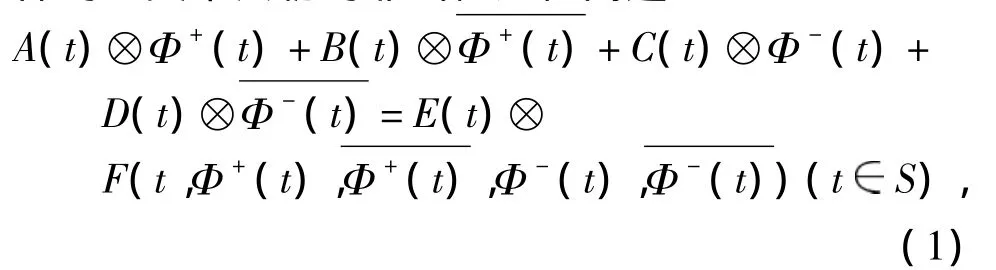
证明了其解的存在性,给出了解的积分表达式,推广了文献[4]中有关边值问题的一些结果.
1 预备知识
用2表示四元数空间,设Ω是2中一有界区域,其边界∂Ω=S是一光滑曲面.用Cβ(S)表示S上有界Hölder连续函数所构成的函数集,其Hölder指数为 β(0<β<1).对∀φCβ(S),定义模C(φ)+H(φ),其中 C(φ).显然 C(S)构成一个 Baβnach 空间,且对∀φ1,φ2Cβ(S),易得
定义 1[4]设 φ(ζ)C(S)(0< β <1),称函β数ψ(z)为Cauchy型积分,其中
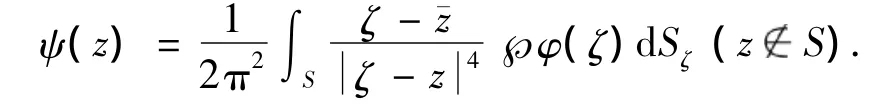
引理 1[4]当 tS时,在Cauchy主值意义下,有
引理2[4](Plemelj公式)用 Ω+表示 Ω,Ω-表示¯Ω的余集.当z从Ω+和 Ω-分别趋近t(S)时,定义1中的函数ψ(z)的极限存在,分别记为ψ+(t)和ψ-(t),且满足:

引理 3[4]设 φ(ζ)C(S)(0 < β <1),则βCauchy型积分 ψ(z)的边界值 ψ±(ζ)Cβ(S),并且ψ(z)Cβ(Ω±).
引理4 设 ζ,t1,t2S,有

2 正则函数向量
设 F(t)=(f1(t),f2(t),…,fn(t)),G(t)=(g1(t),g2(t),…,gn(t))(fi(t),gi(t)Cβ(S),i=1,…,n)是函数向量,定义加(减)法运算和乘法运算如下:F(t)±G(t)=(f1(t)±g1(t),…,fn(t)±gn(t)),F(t)⊗G(t)=(f1(t)g1(t),…,fn(t)gn(t)).
定义函数向量的绝对值为:
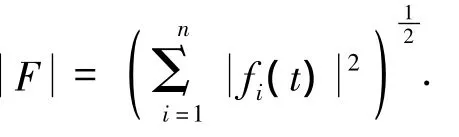
用Cnβ(S)表示S上依绝对值Hölder连续的函数向量的集合,其Hölder指数都为β(0<β<1),连续是指每个分量都连续.对∀FCnβ(S),定义C(F)+H(F),其中 C(F)=sup,H(F)=.容易证得下述结果:
引理5(1)Cnβ(S)按范数构成一个Banach空间,且
定义2 若fi(x)(xΩ,i=1,…,n)是正则函数,则称 F(x)=(f1(x),f2(x),…,fn(x))是 Ω 上的正则函数向量.
由引理2易得正则函数向量的Plemelj公式:

其中(PF)(t)=((Pf1)(t),…,(Pfn)(t)).
3 正则函数向量的非线性边值问题
设Ω是具有光滑Liapanov边界S的有界区域,记号 Ω+和 Ω-同引理 2.设 A(t)=(a1(t),…,an(t)),B(t)=(b1(t),…,bn(t)),C(t)=(c1(t),…,cn(t)),D(t)=(d1(t),…,dn(t)),E(t)=(e1(t),…,en(t)),函数向量 F(t,Φ+(t)=(f1,…,fn)在S×2×2×2×2连续.我们要找在Ω±上正则,在上连续,且满足Φ-(∞)=0的函数向量Φ(z)=(φ1(z),…,φn(z)),使其满足式(1)的边界条件,称此边值问题为问题N.
定义算子 θφi=Pφi(i=1,…,n);θφ =(θφ1,…,θφn).将此代入式(1)整理得:(A+C)⊗θφ +(B+D)⊗θφ+
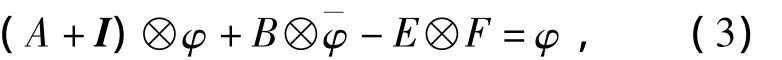
其中I为各分量为1的常数向量.引入算子Lφ=(A+C)⊗θφ+(B+D )+(A+I)⊗φ+B⊗¯φ-E⊗F,故式(3)可写成:则边值问题N转化为求解积分方程(4).

下面设S是光滑定向的Liapunov曲面,γ为其Liapunov曲面常数.按其定义,对于S内任意点t,以t为中心,γ(或小于γ的正数)为半径的超球把S分成两部分,它们分别位于超球内外,并且与过t的法线相平行的直线和S在超球内部分的交点不超过一个.以t为原点建立局部坐标系,ξ4轴放在沿S在t点处外法线上,设S包含在超球内的部分为S1,则S1的方程可表示为 ξ4= ξ4(ξ1,ξ2,ξ3).记 S1在 t点切平面内的投影区域为π1,设S1上任意点ζ处外法
定理1 设 φi(t)Cβ(S)(0 < β <1,i=1,…,n),S是光滑定向的Liapunov曲面,则存在与φ无关的正常数G0,使得(下面的记号中,G1,G2,…都同样表示与φ无关的正常数).

则tS

对于I1,由前面对Liapunov曲面的讨论有

类似地,对于I2有

下面估计I3:

对于L1,因积分是正常积分,且积分区域S2有界,故
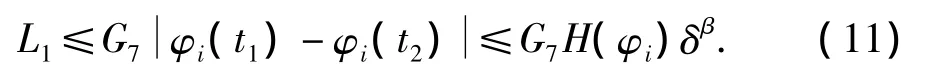

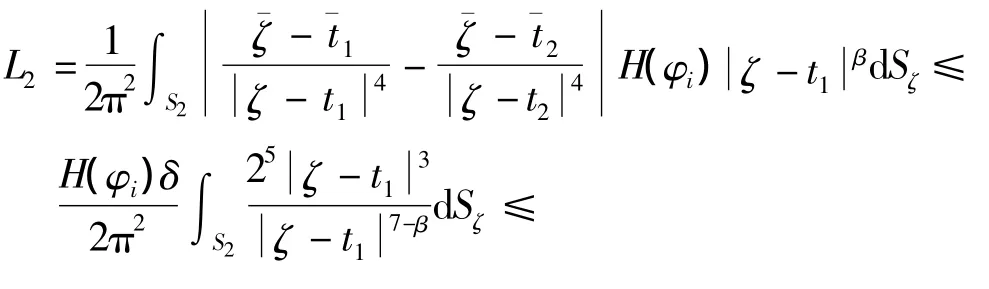
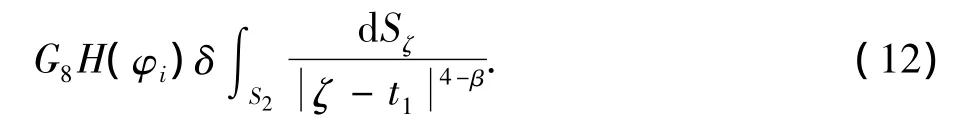
又因为S有界,故取正常数N,使得以t1为中心,N为半径的超球包含S,利用球坐标变换有:

由式(10)、(11)、(13)可得:

由式(7)~(9)、(14),结合三角不等式可得:

其次考虑3δ≥γ的情况.由式(7)有

故根据式(15)、(16),不管哪种情况都可得

推论1 当 φi(t)Cβ(S)时,0 <β <1,有
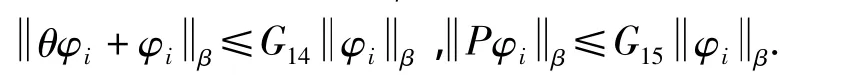
证明 由定理1和引理5,有
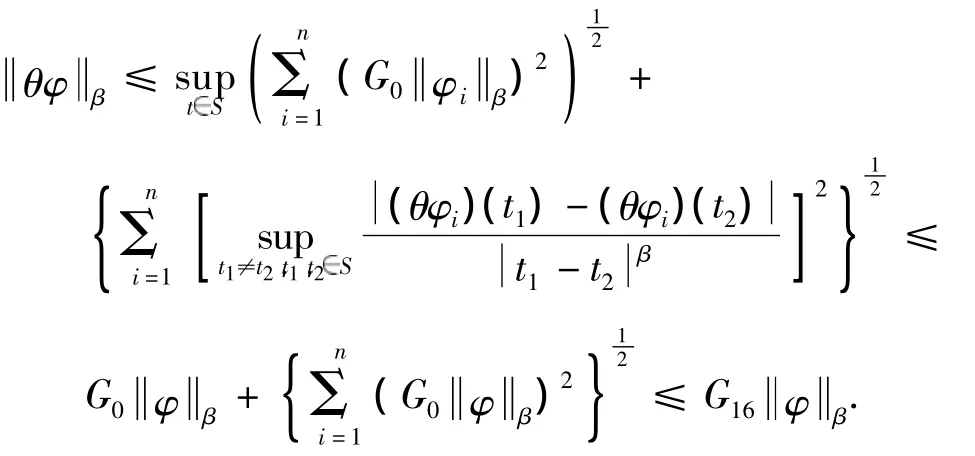
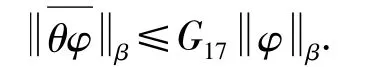
推论3 设 φ(t)满足定理2的要求,Pφ=(Pφ1,…,Pφn),则有
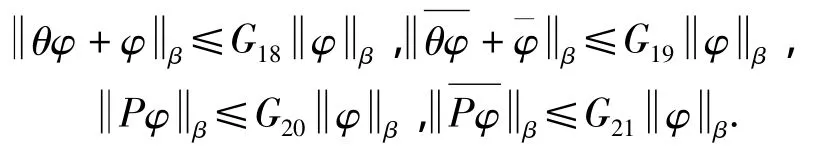
定理3 设问题N中A(t),B(t),C(t),D(t),E(t)Cn(S),函数向量F满足:β
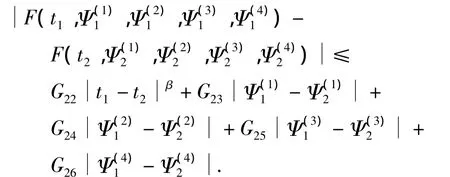
设 f(t0,0,0,0,0)=0,t0为 S 上一定点,=δ,则当0<δ<,问题N可解,且解表达式如式(22).
证明 记HM=≤M}.首先证明算子L映HM到自身.由定理2、引理5及推论2可得:

下证L在HM上连续.对任意的一致收敛函数向量列{φ(m)}⊂HM,设在S上一致收敛于函数向量φHM(指函数向量列{φ(m)}的每一个分量形成的函数列{φ(im)}都一致收敛于函数向量φ的相对应的分量{φi},i=1,…,n),即对∀ε >0,当 n 足够大时,恒有

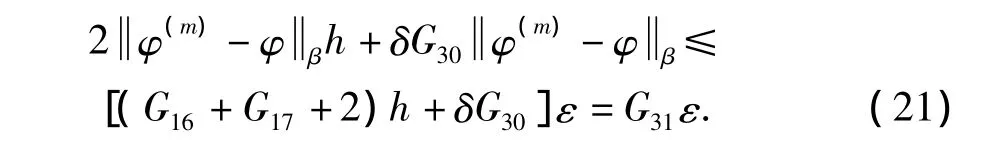
所以L是映射HM到自身的连续映射.根据Arzela-Ascoli定理知,HM是连续空间中Cn(S)的紧子集.因此连续映射L映射Cn(S)中的闭凸集HM到自身,并且 L(HM)也是 Cn(S)中的紧子集.再利用Schauder不动点定理知,至少存在一个适合奇异积分(4),所以问题N至少存在一解,并且解的积分表达式:
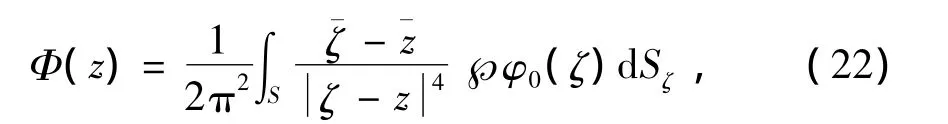
显然满足Φ(∞)=0.
[1]GROSSF,TZE H C.Complex and quaternionic analyticity in chiral and gauge theories[J].Ann of Phys,1980,128:29-130.
[2]GÜRLEBECK K,SPRÖSSIG W.Quaternionic analysis and elliptic boundary value problem[M].Boston:Birkhäuser,1990.
[3]SUDBERY A.Quaternionic analysis[J].Math Proc Comb Phil Soc,1979,85:199-225.
[4]杨丕文.四元数分析与偏微分方程[M].北京:科学出版社,2009.
[5]谢永红,杨贺菊.Clifford分析中无界域上向量值函数的非线性边值问题[J].高校应用数学学报,2010,25(2):163-171.

