一类解析函数的Fekete-Szegö不等式

郭 栋，李宗涛，杨家稳

(1．滁州职业技术学院基础部，安徽滁州239000;2．广州民航职业技术学院基础部，广东广州510403)

1 引言与结果

FEKETE和SZEGÖ［1］于1933年证明了如下结果．

且对每个μ等号均能成立．

其中的幂函数取主值．当 θ=0时，Bθ(λ，α，ρ)=B(λ，α，ρ)．文献［2］、［3］讨论了 B(λ，α，ρ)的单叶条件、单叶半径、包含关系、偏差定理、函数的不等式性质和覆盖定理．文献［4］讨论了 B(λ，α，ρ)的Fekete-Szegö不等式．本文研究了 Bθ(λ，α，ρ)的Fekete-Szegö不等式，得到了它的精确结果，文献［4］中的定理1是本文定理1的一个推论，但使用的方法不同．

记

设f(z)=z+a2z2+a3z3+…，φ(z)=

由于

通过计算有

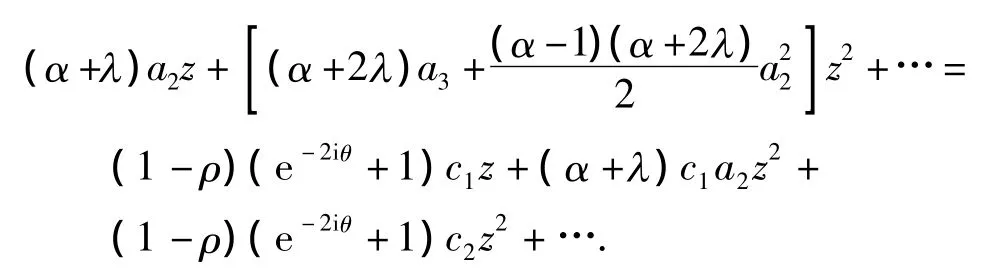
比较系数得

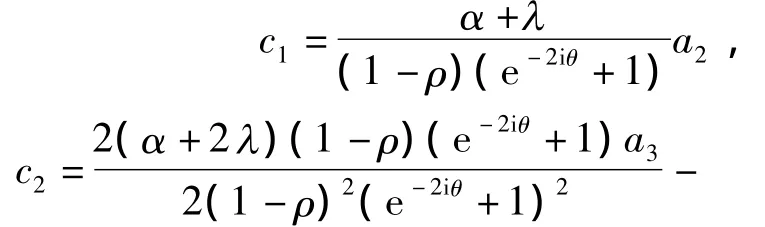
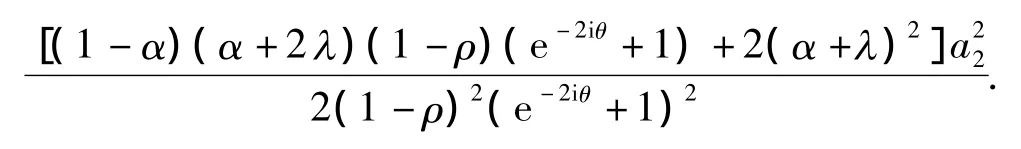
由于 e-2iθ+1=e-iθ(eiθ+e-iθ)=2e-iθcosθ，令u=eiθ/(2cosθ)，于是有

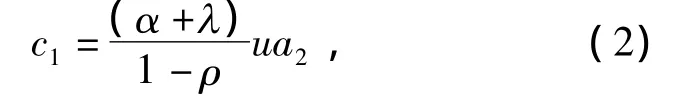
为了导出本文的主要结果，先给出如下引理:

引理1［5］设 φ(z)=c1z+c2z2+c3z3+…在 U内解析且满足，极值函数φ(z)=z2;

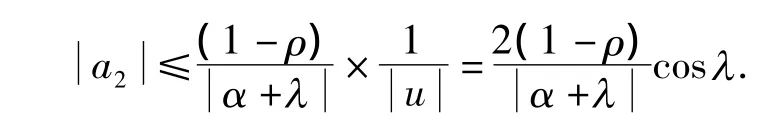
在定理1中令θ=0，得

注释1 推论1就是文献［4］的定理1．

特别地当θ=0时，有

其中，μ1=

2 定理的证明

定理1的证明 利用引理中的估计(ii)，对于

或

令

当(α+λ)(α+2λ)≠0时，有

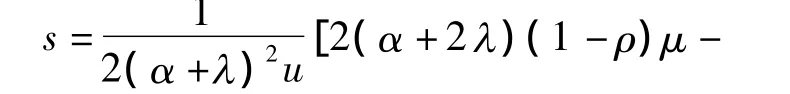
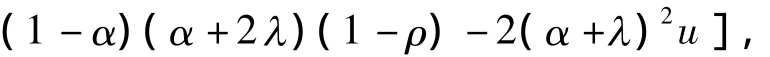
于是

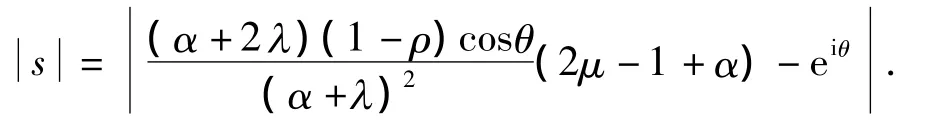
则式(4)可以写成

综上所述，本定理得证．

推论2的证明 当μ是实数时，由于

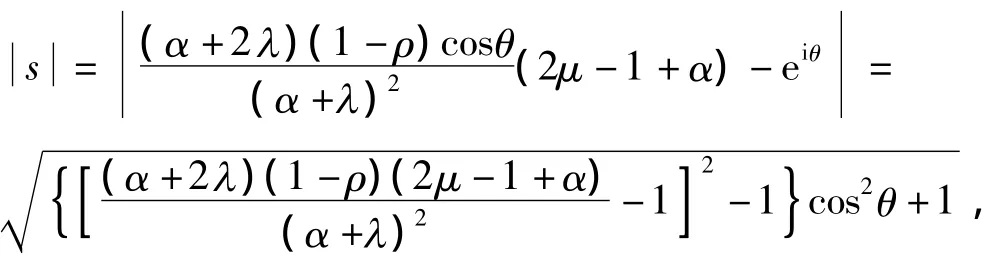
于是

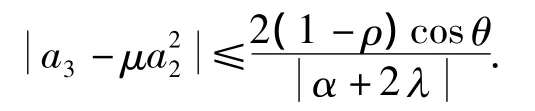
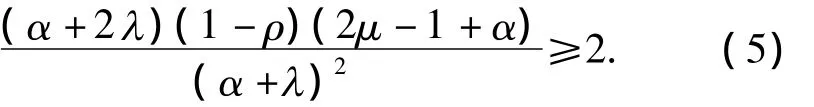
当λ ＞ -α/2，-∞ ＜μ≤(1-α)/2，或λ ＜ -α/2，+∞＞μ≥(1-α)/2时，

综合式(5)、(6)，得

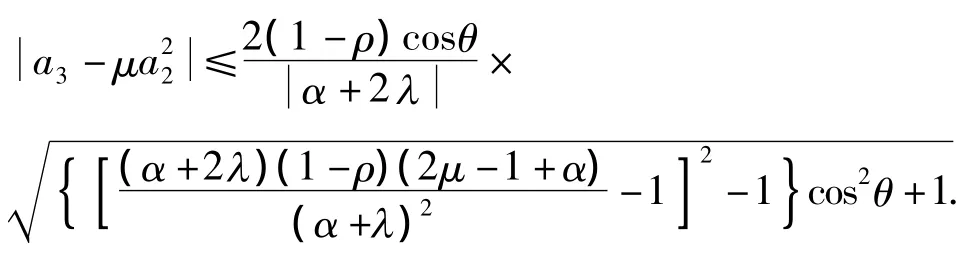
结论得证．

［1］FEKETE M，SZEGÖ G．Eine Bermrkung uberungerade schlichte funktionen［J］．JLondon Math Soc，1933，8:85-89．

［2］LIU Mingsheng．On certain subclass of P-valent functions［J］．Soochow Jof Math，2000，26(2):163-171．

［3］LIU Mingsheng．Properties for some subclasses of analytic functions［J］．Bulletin of the Institute of Math Acdaemia Sinica，2002，30(1):9-26．

［4］郭栋，刘名生．关于解析函数类的Fekete-Szegö问题［J］．华南师范大学学报:自然科学版，2007(2):33-38．

［5］NEHARIZ．Conformalmapping［M］．New York:McGraw-Hill，1952:108．