关于具有给定二分类的单圈二部图的极小能量

杨 勇

(佛山科学技术学院信息科学与数学系，广东佛山528000)

设G是一个n阶简单图，A(G)是G的邻接矩阵，I是n阶单位阵，G的特征多项式φ(G)=det(λIA(G))．设 G 的特征值为λ1，λ2，…，λn，则 G 的能量定义为［1］

在理论化学中，共轭分子的π-电子总能量可通过其分子图近似计算，关于分子图的能量已有许多结果［1-4］．

当G是一个n阶二部图时，则［5］

其中 bi(G)≥0，0≤i≤⎿n/2」．于是，Sachs定理［5］表述为对于任意 1≤i≤⎿n/2」，有

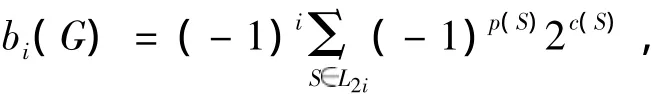
其中L2i是G的2i阶Sachs子图集(Sachs子图是指每个分支要么是圈图，要么是2阶完全图的图)，p(S)是子图S的分支个数，c(S)是子图S中圈图个数．另外，规定b0(G)=1．显然 b1(G)等于G的边数．为了叙述方便，令bi(G)=0，如果i＜0或者i＞⎿n/2」．众所周知，E(G)可表示成下列Coulson积分形式［4］

二部图中的拟序关系“≿”和“≻”如下定义:设G1和G2都是二部图．如果对于任意1≤i≤⎿n/2」，都有 bi(G1)≥bi(G2)，则称 G1≿G2．如果 G1≿G2，并且存在某个k使得bk(G1)＞bk(G2)，则称G1≻G2．由式(1)，E有下面的增属性:

因此，依据能量，二部图的排序可通过它们的特征多项式系数确定．

设G是一个连通二部图，则它的顶点集能唯一地划分成2个子集V1和V2，使得它的每条边的2个端点分别在V1和V2中，(V1，V2)称为G的二分类．进一步地，则称G是二分类(p，q)的．具有n(≥3)个顶点n条边的连通图称为单圈图．

GUTMAN［6］开始在给定的一类图中研究确定具有最小能量和最大能量的图，更多结果参看文献［7］-［8］．当 p=2 或 p≥4 时，LI和 ZHOU［9］确定了给定二分类(p，n-p)的单圈二部图中具有最小能量的图，其中p≤⎿n/2」;当p=3时，他们指出图B1n或B2n(图1)具有最小能量．下面将对p=3的情形做进一步的探讨．

1 预备知识

若uv是G的一条割边，则由文献［1］，有φ(G)=φ(G-uv)-φ(G-u-v)，从而有

引理1 设G是一个二部图．若uv是G的一条割边，则

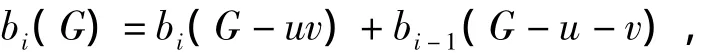
特别是，若u是G的一个悬挂点，而v是其唯一的相邻顶点，则

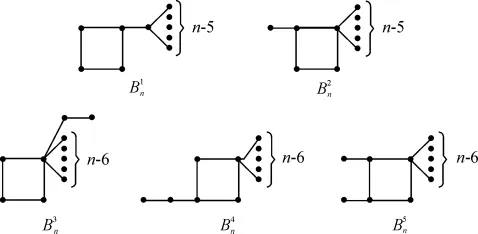
图1 图 Bkn(k=1，2，…，5)Figure 1 Graphs Bkn(k=1，2，…，5)

由引理1，得

引理2 设G是一个二部图．若H是从G中删除至少一条割边所得到的生成子图，则G≻H．

引理3 设G，G'都是二部图，u(相应有u')是G(相应有G')的一个悬挂点，v(相应有v')是其唯一的相邻顶点．若G-u≿G'-u'且G-u-v≻G'-u'-v'，或者 G-u≻G'-u'且 G-u-v≿G'-u'-v'，则G≻G'．

2 主要结果

对于图G和H，若G与H不同构，记为G≠H．设Pn和Cn分别是n阶路图和圈图．

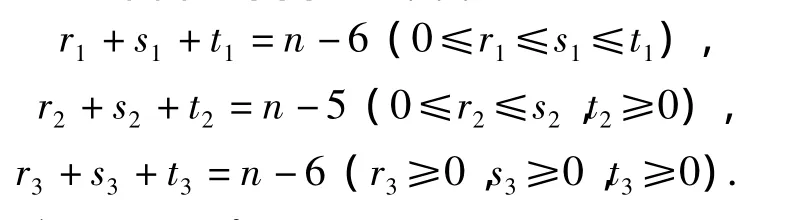
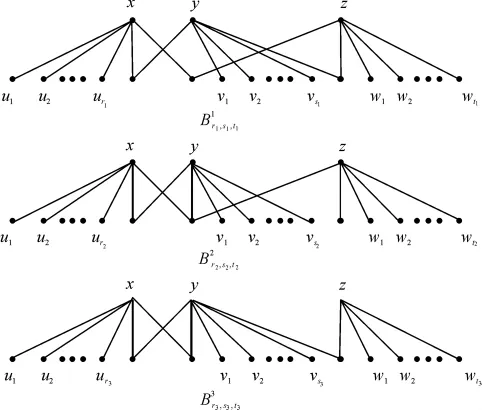
图2 图Figure 2 Graphs

引理 4［9］设 G)且 G≠B1n，B2n，其中 n≥7，则 G≻B2n．

(i)若 G≠B17，B27，B37，则 G≻B37．

(ii)若 G≠B17，B27，B37，B47，B57，则 G≻B47．

证明 容易看出，给定二分类(3，4)的任何一个7阶单圈二部图一定同构于下列图之一:图Bk7和Hi(k=1，2，…，5;i=1，2，3)，其中 H1是在一个四角形的某个顶点上加一条长为3的路所得到的图，H2是在一个四角形的2个相邻顶点上分别加一条悬挂边和一条长为2的路所得到的图，H3是在一个六角形的某个顶点上加一条悬挂边所得到的图．由Sachs定理，得

因此，引理结论成立．

用Sn表示n阶星图，Yn表示在星图Sn-1的某个悬挂点上加一条悬挂边所得到的n阶树图．顶点不相交的图 G1，G2，…，Gl的并，记为 G1∪G2∪…∪Gl，特别是，当 Gj=G(j=1，2，…，l)时，记为 lG．

证明 对n用数学归纳法．当n=7时，由引理5(i)，结论显然成立．假设当n≥8时，结论对n-1阶图成立．设)．注意到G一定是图2中的3种图之一．

情形1 G=B1r1，s1，t1．由于 r1+s1+t1=n-6，0≤r1≤s1≤t1，n≥8，故 t1≥1．显然，G-w1G-w1-z是无圈图且包含一条路P5，以及G-w1≠．由归纳假设，得 G-w1≻=B3n-u'，其中u'是B3n的一悬挂点，且它唯一的邻点v'是非2度顶点．由引理2知G-w1-z≿(n-7)P1∪P5≻(n-7)P1∪P2∪P3=B3n-u'-v'．因此，由引理 3，得 G≻B3n．

情形2 G=B2r2，s2，t2．设 r2≥1，则 s2≥1，G-v1(n-1)，G-v1≠，以及 G-v1-y是无圈图且包含一颗树Y5．由归纳假设，得G-v1≻B3n-1，而由引理 2，又有 G-v1-y≿(n-7)P1∪Y5≻(n-7)P1∪P2∪P3．因此，由引理 3，得 G≻B3n．

设 r2=0．由于 G≠B1n，B2n且 n≥8，故 s2，t2≥1，max{s2，t2}≥2．若 s2≥t2，则 s2≥2，G-v11)，G-v1≠，以及G-v1-y是无圈图且包含一条路P5，于是类似情形1的讨论，有G≻B3n．若 t2≥s2，则 t2≥2，G-w1)，G-w1≠，以及G-w1-z包含一个子图P45．由归纳假设，G-w1≻B3n-1，而由引理2，知 G-w1-z≿(n-7)P1∪P45．由于 b1(P45)=5 ＞3=b1(P2∪P3)且 b2(P45)=b2(P2∪P3)=2，故 P45≻P2∪P3．因此，G-w1-z≻(n-7)P1∪P2∪P3，由引理 3，知 G≻B3n．

情形3 G=B3r3，s3，t3．若 r3≥1，则 G-u11)，G-u1≠，以及G-u1-x是无圈图且包含一颗树Y5．由归纳假设，得G-u1≿B3n-1，而由引理 2，又有 G-u1-x≿(n-7)P1∪Y5≻(n-7)P1∪P2∪P3．因此，由引理3，得 G≻B3n．

设 r3=0．由于 G≠B3n，故 t3≥1，G-w11)，G-w1≠B1n-1，B2n-1，以及G-w1-z包含一个子图P45，于是类似以上的讨论，得G≻B3n． □

证明 对n用数学归纳法．当n=7时，由引理5(ii)，结论显然成立．假设当n≥8时，结论对n-1

情形1 G=B1r1，s1，t1．由于 r1+s1+t1=n-6，0≤r1≤s1≤t1，n≥8，故 t1≥1．显然 G-w1(n-1)，G-w1≠Bkn-1(k=1，2，…，5)，以及 G-w1-z是无圈图且包含一条路P5．由归纳假设，得G-w1≻B4n-u'，其中u'是B4n的一悬挂点，且它唯一的邻点v'是非2度顶点．由引理2有G-w1-z≿(n-7)P1∪P5．显然 P5≻Y5．因此，G-w1-z≻(n-7)P1∪Y5=B4n-u'-v'，于是由引理 3，得 G≻B4n．

情形2 G=B2r2，s2，t2．设 r2≥1，则 s2≥1．若 G=)=8 ＞6=b3(B49)，b4()=b4(B49)=0，于是 G≻B49．设G≠B22，2，0．显然 G-v1，G-v1≠Bkn-1(k=1，2，…，5)，以及 G-v1-y是无圈图且包含一颗树Y5．由归纳假设，得 G-v1≻B4n-1，而由引理 2，得G-v1-y≿(n-7)P1∪Y5．因此，由引理 3，得 G≻B4n．

设 r2=0．由于 G≠B1n，B2n且 n≥8，故 s2，t2≥1，max{s2，t2}≥2．若 s2≥t2，则 s2≥2，G-v1(n-1)，G-v1≠Bkn-1(k=1，2，…，5)，以及 G-v1-y 是无圈图且包含一条路P5，于是类似情形1的讨论，得 G≻B4n．若 t2≥s2，则 t2≥2，G-w1(n-1)，G-w1≠Bkn-1(k=1，2，…，5)，以及 G-w1-z包含一个子图P45．由归纳假设，得G-w1≻B4n-1，而由引理2，又得 G-w1-z≿(n-7)P1∪P45．由于 b1(P45)=5 ＞4=b1(Y5)，b2(P45)=2=b2(Y5)，故 P45≻Y5．因此，G-w1-z≻(n-7)P1∪Y5，于是由引理3，得 G≻B4n．

情形3 G=B3r3，s3，t3．若 t3≥2，则 G-w1(n-1)，G-w1≠Bkn-1(k=1，2，…，5)，以及 G-w1-z包含一个子图P45，于是类似以上的讨论，得G≻B4n．

设 t3=1．由于 n≥8，故 r3≥1 或 s3≥1．若 r3≥s3，则 r3≥1，G-u1≠Bkn-1(k=1，2，…，5)，以及 G-u1-x是无圈图且包含一颗树 Y5，于是 G≻B4n．若s3≥r3，则 s3≥1，G-v1(n-1)，G-v1≠Bkn-1(k=1，2，…，5)，以及 G-v1-y 是无圈图且包含一个子图P3∪P3．由归纳假设，得G-v1≻B4n-1，而由引理2，又得 G-v1-y≿(n-8)P1∪P3∪P3．由于 b1(P3∪P3)=4 和 b2(P3∪P3)=4，故 P3∪P3≻P1∪Y5．因此，G-v1-y≻(n-7)P1∪Y5，于是由引理 3，得G≻B4n．

设 t3=0．因为 G≠B3n，B4n，所以 r3，s3≥1．显然(n-1)，G-v1≠Bkn-1(k=1，2，3，5)，以及G-v1-y是无圈图且包含一个子图S4∪P2．由归纳假设，得G-v1≿B4n-1，而由引理 2，又得 G-v1-y≿(n-8)P1∪S4∪P2．因为 b1(S4∪P2)=4，b2(S4∪P2)=3，所以 S4∪P2≻P1∪Y5．因此，G-v1-y≻(n-7)P1∪Y5，于是由引理 3，得 G≻B4n． □

下述引理8是文献［9］的猜想，这里将给出严格的证明．

引理8 对于n≥7，有E(B1n)＜E(B2n)．

证明 由Sachs定理，有

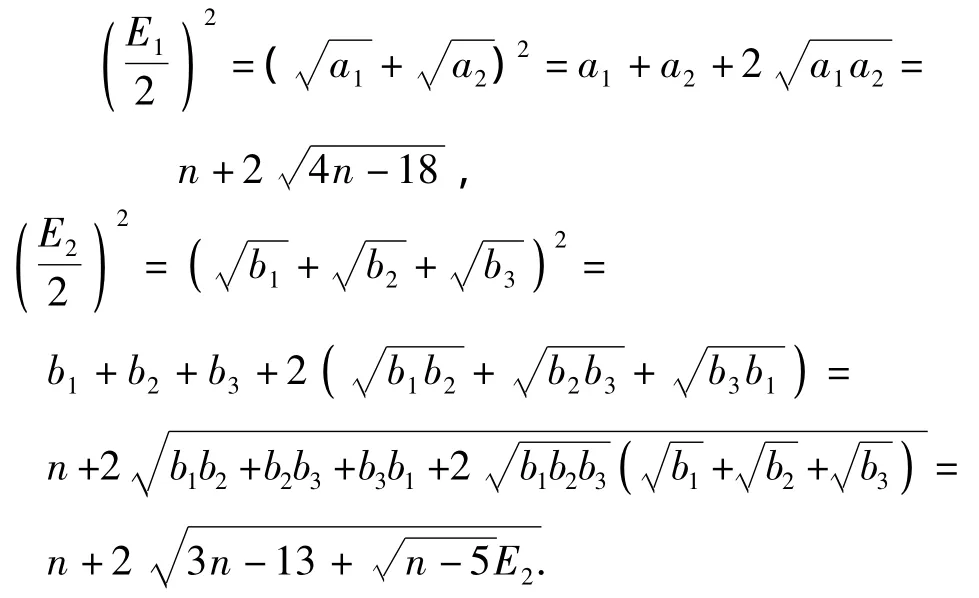
容易看出，若要E1＜E2成立，只需4n-18＜3n-13+，也即E2＞．由文献［2］知对于任意一个没有孤立顶点的n阶图G，有E(G)≥2故E2＞成立．

由引理4、引理6～引理8和式(2)，有

定理1 设n≥7，则

(i)图 B1n，B2n和 B3n分别是(n)中唯一具有最小、第二小和第三小能量的图．

(ii)图 B4n是(n)B5n中唯一具有第四小能量的图．

由Sachs定理，有φ(B5n)=λn-nλn-2+(4n-19)λn-4-(2n-11)λn-6．从上述特征多项式的λn-4和λn-6的系数，容易看出拟序关系“≻”不能用于比较图B4n和B5n的能量．

［1］GUTMAN I．The energy of a graph［J］．Ber Math-Statist Sekt Forsc hungszentrum Graz，1978，103:1-22．

［2］GUTMAN I．The energy of a graph:Old and new results［M］∥BETTEN A，KOHNERT A，LAUE R，et al．Algebraic Combinatorics and Applications．Berlin:Springer-Verlag，2001:196-211．

［3］GUTMAN I．Topology and stability of conjugated hydrocarbons:The dependence of totalπ-electron energy on molecular topology［J］．JSerb Chem Soc，2005，70:441-456．

［4］GUTMAN I，POLANSKY O E．Mathematical concepts in organic chemistry［M］．Berlin:Springer-Verlag，1986．

［5］CVETKOVI'C D，DOOB M，SACHSH．Spectra of graphs-theory and application［M］．Heidelberg:Johann Ambrosius Barth，1995．

［6］GUTMAN I．Acyclic system with extremal Hückelπ -electron energy［J］．The oret Chim Acta，1977，45:79-87．

［7］HOU Y．Unicyclic graphs with minimal energy［J］．J Math Chem，2001，29:163-168．

［8］RADA J，TINEO A．Polygonal chains with minimal energy［J］．Lin Algebra Appl，2003，372:333-344．

［9］LI F，ZHOU B．Minimal energy of bipartite unicyclic graphs of a given bipartition［J］．MATCH Commun Math Comput Chem，2005，54:379-388．