精确的快速极坐标谐波变换*

沃焱 徐角

(华南理工大学计算机科学与工程学院，广东广州510006)

旋转和缩放不变的模式表示是基于内容的图像检索、模式识别等应用领域的难点之一．在许多实际应用中，图像被缩放、旋转后仍被视为内容是相同的．研究者们已经提出了许多旋转不变特性的表示方法，其中包括比较广泛使用的Zernike矩(ZMS)、伪 Zernike矩(PSMS)［1］．Zernike 矩、伪 Zernike 矩具有旋转不变性，还具有对噪声不敏感的特性，能较好地表达图像特征，被广泛地应用于数字水印，人脸/字符识别，纹理分类、图像检索等领域［2-7］．尽管如此，由于计算Zernike矩、伪Zernike矩需多次阶乘运算，随着阶数增加，计算量和计算数值呈指数级增长，不适合计算机存储，且多次乘除运算易产生精度损失，故对高阶矩而言，不可避免地会存在迭代累计误差，进而影响图像重建精度．针对Zernike矩在笛卡尔坐标下存在的计算精度问题，Xin等［8-9］通过像素重排的方式在极坐标下计算Zernike矩，消除了几何误差和数值积分误差，极大地提高了Zernike矩的计算精度．

Yap 等［10］提出了极坐标谐波变换(PHT)，与Zernike、伪Zernike矩相比，PHT保留了正交性、旋转不变性，且核函数形式简单，同时具有数值稳定性．但PHT在极坐标下定义，计算图像的PHT矩时需将数字图像由笛卡尔坐标转换到极坐标，坐标转换离散化时会产生计算误差．在计算PHT内核系数时需要多次计算三角函数，从而使PHT计算速度较慢．Yang等［11］利用三角函数的对称性减少PHT内核系数的计算速度，但没有解决离散PHT计算误差问题，且在计算PHT内核系数时仍需多次三角函数计算．

针对上述问题，文中将以极坐标取代笛卡尔坐标计算Zernike矩的方法推广到PHT矩的计算中，提出在极坐标下具有缩放旋转不变的PHT矩计算方法，并对极坐标进行设计和规划，以消除笛卡尔坐标下PHT矩计算中存在的几何误差和积分近似误差．为了提高运算速度，在计算过程中利用三角函数的对称性等相关性质减少三角函数的计算次数，并利用查找表的方式进一步提高计算速度，同时消除迭代累计误差，提高图像的重建精度．根据不同变换核，极坐标谐波变换可分为极复指数变换(PCET)、极正弦变换(PST)和极余弦变换(PCT)3种变换．文中在算法推导的过程中选用PCET．

1 PHT极坐标谐波变换

1．1 极坐标谐波变换定义

对于一幅连续域上的图像，将横坐标和纵坐标投影到［-1，1］区间．PHT 在极坐标下的定义式为［10］

式(1)中，［·］*表示复共轭，Mnl称为图像 f的 PHT(n，l)矩．式(2)表明基函数 Hnl(r，θ)能分解成半径分量Rn(r)和角度分量eilθ，n表示阶数，l表示重复数，n、l为任意整数，==0，1，…，∞．极复指数变换PCET中

极余弦变换PCT中，Rn(r)=sin(nr2);极正弦变换PST中，Rn(r)=cos(nr2)．

PHT基函数具有正交性，且任何图像都可用式(4)重建:

如果仅用n，l的一个子集重建，可以得到图像的一个近似，随着n、l增加可得到更加精确的重建图像．

1．2 PCET 的离散计算

数字图像都是离散的，因此需将式(1)转换成离散形式．由于PCET是定义在极坐标下的，在迪卡尔坐标下定义PCET有如下形式:

式中，H'nl(x，y)=H'nl(rcosθ，rsinθ)≡Hnl(r，θ)，f'(x，y)=f(rcosθ，rsinθ)≡f(r，θ)．

假设图f是一幅N×N的离散图像，其定义域为 g［i，j］，其中 i=1，2，…，N，j=1，2，…，N．将图像映射到区间(xi，yj)∈［-1，1］×［-1，1］．其中，xi=(2i-N-1)/N，yj=(2j-N-1)/N，则有

其中，xi，yj满足+≤1，

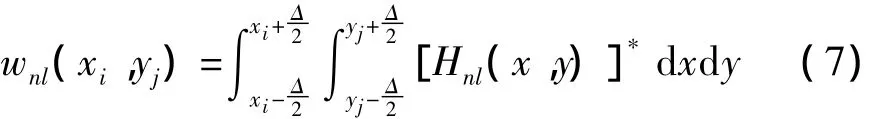
其中Δ=2/N是像素的宽度．在笛卡尔坐标系下无法得到式(7)的准确值，只能由式(8)得到估计值，如此这就产生了数值积分误差:

将估计值代入式(6)，得到PCET的离散形式［10］:

式(9)是笛卡尔坐标下离散PCET的计算公式．利用式(9)计算PCET时，会产生数值积分误差．另外，在计算PCET时如按数字图像的像素离散时会产生几何误差，这与Zernike矩相似．几何误差产生的原因是正方形的单位像素组成的块不可能恰好覆盖一个单位圆．只要采用笛卡尔坐标系，几何误差就是不可避免的，因此，要提高PCET的计算精度就需要减少几何误差和数值积分误差．

2 快速极坐标下的PCET离散计算

2．1 极坐标划分与像素插值

若图像大小为N×N，则需计算PCET的圆型区域的半径为N/2．先将圆等分成V个扇区，沿径向将圆分成U层圆环区域，依次将第 u(u=1，2，3，…，U)层的V个扇区分别等分成为2u-1，个块则第u个圆环被等分成V(2u-1)个像素块．需计算PCET的圆型区域被划分得到VU2个像素块．文中取U=N/2，当V=4时划分结果如图1(a)所示．每个扇区表示为 Ωuv，如图 1(b)所示，u=1，2，…，U;v=1，2，…，V(2u-1)．扇区 Ωuv表示极坐标像素(ρuv，θuv)和分别表示 Ωuv的开始和结束半径和分别表示 Ωuv的开始和结束角度，ρuv=(+)/2，=+)/2．

图1 笛卡尔坐标与极坐标下计算PHT的像素分布Fig．1 Pixels distribution in Cartesian coordinates and polar coordinates for PHT computation

图像单位圆被分成VU2个扇区，每个扇区的大小是/(VU2)，U和V的取值要适当．VU2小则计算量小，对图像信息的表达误差大;反之则计算量大，对图像信息的表达误差小．

极坐标中的像素位置(ρuv，θuv)与笛卡尔坐标中的像素位置不吻合，需要通过插值的方式来解决这个问题．文中采用双三次插值方法，双三次插值方法具有三阶精度，可以满足式(6)中定义的估计方法．对划分后的像素块Ωuv使用式(10)插值得到极坐标下的图像f'各像素的值:

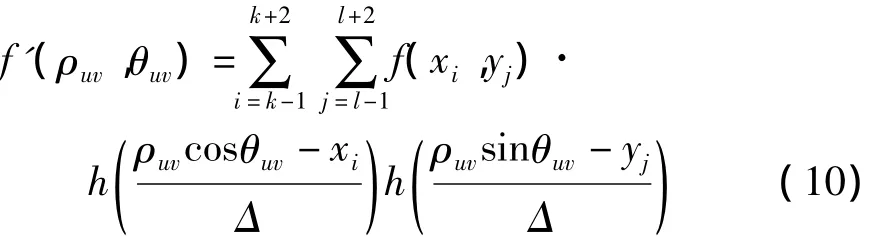
式中:k=「ρuvcosθuv/Δ⏋ +N/2;l=「ρuvsinθuv/Δ⏋ +N/2;f为笛卡尔坐标下的图像;h(·)是双三次插值的1-D核函数，

2．2 极坐标下的PCET计算

由式(6)、(7)可知，插值得到的图像f'的PCET可利用式(11)进行计算:

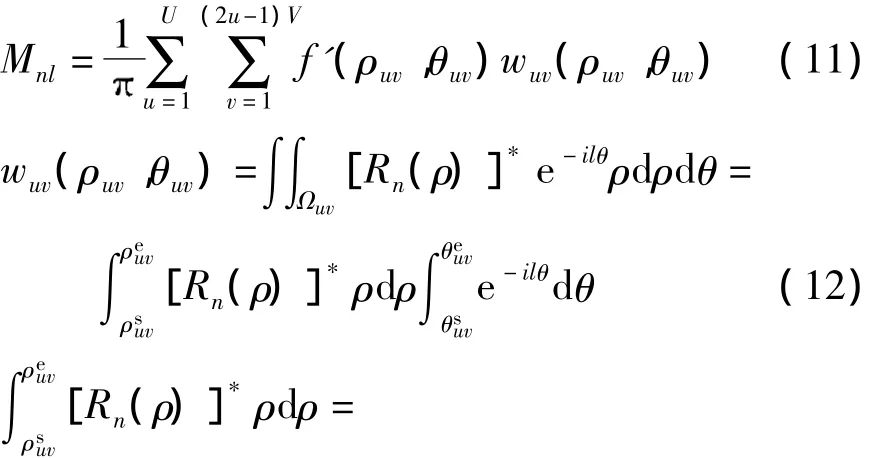
式(13)是PCET基的半径分量计算公式，式(14)是PCET基的角度分量计算公式．由复数与三角函数的关系，式(13)中，

式(14)中，

直接利用式(13)-(16)计算一个像素点的PCET基的半径分量和角度分量时，分别需要4次三角函数计算、1次复数加法，这使得PCET的计算时间较长．

2．3 PCET基的快速计算

借鉴快速傅里叶变换(FFT)的思想，根据三角函数的周期性和对称性可提高PCET基的计算速度．cos(lθ)和 sin(lθ)是周期为 2/l的周期函数，由三角函数的周期性和对称性可得:

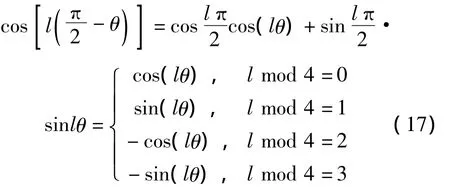
同理可得表1．

表1 极坐标像素对称点的三角函数关系Table 1 Trigonometric relations of symmetric pixels in polar coordinates

表1描述了如图2所示的8个对称点a1，a2，…，a8的三角函数关系:

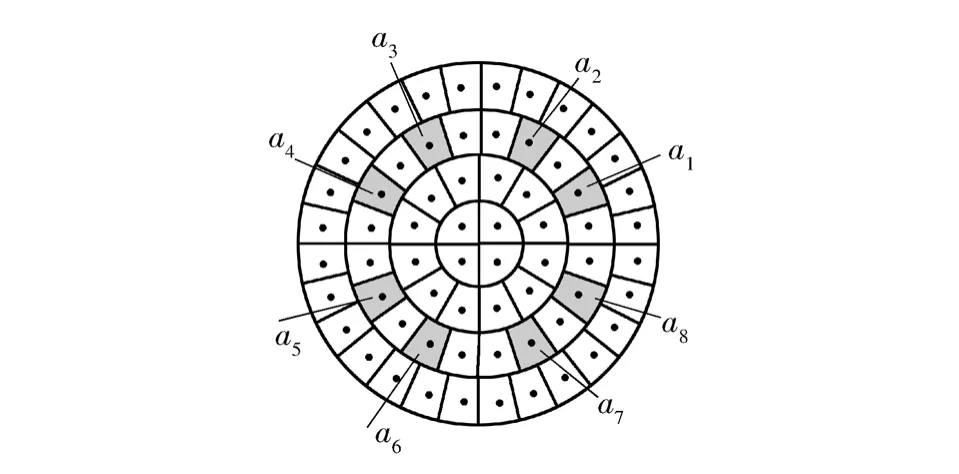
图2 极坐标像素对称点Fig．2 Symmetric pixels in polar coordinates

由表1和式(14)、(15)可得，当l mod 4=0时，

利用对称性计算PCET基可以减少三角函数的计算次数，由式(19)可见，计算8个像素点的PCET基的角度分量时需要4次三角函数计算、1次复数加法．

2．3．1 PCET基中角度分量的快速计算在极坐标划分时，划分扇形区域V取4，如图1(a)所示，因而对于1≤u≤U，1≤v≤4(2u-1)，有

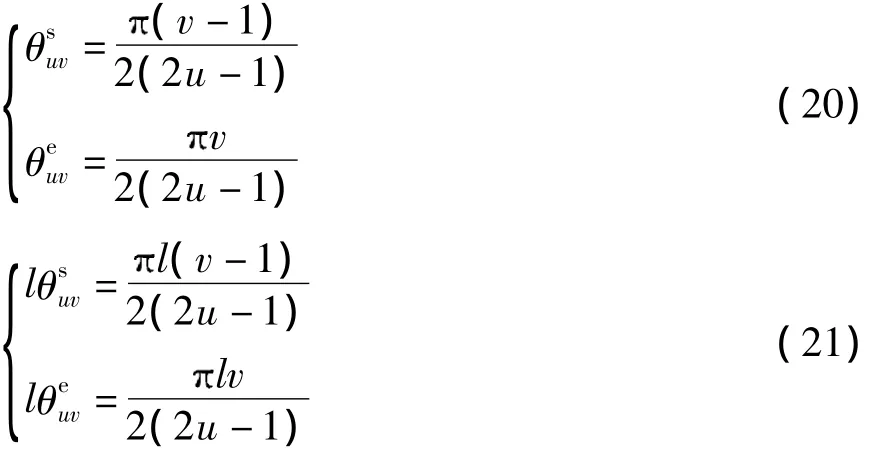
将式(23)代入(19)中，可得

计算 sin(vβu)、cos(vβu)(1≤u≤U，1≤v≤4(2u-1))，存储在2个矩阵中，记为 A、B．A、B 中的元素 Au，v，Bu，v分别表示 sin(vβu)、cos(vβu)．当 l＞ 0时，sin(lvβu)、cos(lvβu)分别在矢量 Au和 Bu中找第lv个单元的值．第u个环被分成4(2u-1)个扇区，因此lv＞4(2u-1)时，lv需要对 4(2u-1)取模，则sin(lvβu)、cos(lvβu)分别在 Au、Bu中是第 lv mod 4(2u-1)个元素 Au，lvmod4(2u-1)，Bu，lvmod4(2u-1)．如果l＜0，因为 sin(- α)=-sinα，cos(- α)=cosα，则 sin(lvβu)为 -Au，lvmod4(2u-1)，cos(lvβu)为Bu，lvmod4(2u-1)．利用查找表，式(24)可表示为

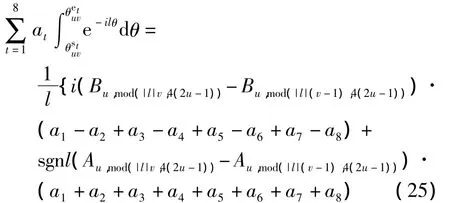
其中，sgnl表示l的符号．

同理，当l mod 4=1时，

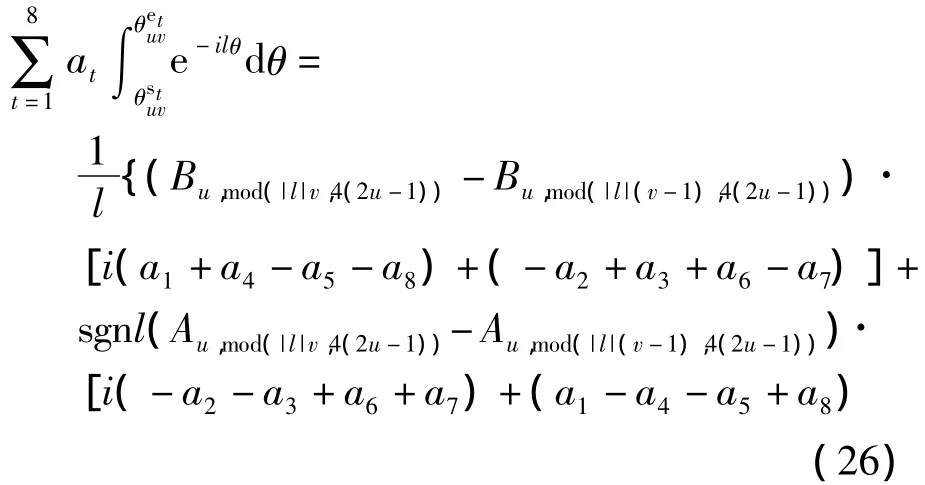
当l mod 4=2时，

当l mod 4=3时，

当v=u，0 ＜u＜U 时，对称点为4个，分别是a1，a3，a5，a7．则利用式(25)-(28)时，将 a2，a4，a6，a8均视为0．

2．3．2 PCET基中径向分量的快速计算

与角度分量的计算相同，半径分量也可用查找表的方式快速计算．令γu=2u/U2，将式(22)代入式(15)中，则有

计算 sinγk、cosγk(1≤k≤U2)，存储在 2 个一维向量中，记为 C、D．其中元素 Cu、Du分别表示sinγu、cosγu．当 n ＞0 时，sin(nuγu)、cos(nuγu)分别在矢量C、D中找第 nu2个单元的值．当 nu2＞U2时，nu2需要对 U2取模，则 sin(nuγu)、cos(nuγu)分别在 C、D 中是元素 Cnu2modU2、Dnu2modU2．当 n ＜0 时，sin(nuγu)为-Cnu2modU2，cos(nuγu)为 Dnu2modU2．利用查找表，式(29)表示为

3 实验结果与分析

3．1 极坐标下计算PCET的重建精度

对大小为256×256的Lena图像分别在笛卡尔坐标下和极坐标下计算PCET后对图像进行重建，计算PCET时，≤≤K．K 分别为60、70、80 的基于笛卡尔坐标的PCET重建图像和基于极坐标的PCET重建结果如图3、4所示．从图中可以看出，基于笛卡尔坐标的PCET重建图像沿单位圆边界的一些错误的像素是非常明显的，随着K的增大，错误像素数量迅速增加．然而，这种错误的像素在基于极坐标的PCET重建图像中不存在．

图3 基于笛卡尔坐标的PCET重建结果Fig．3 Image reconstruction from PCETs based on Cartesian method

图4 基于文中的极坐标的PCET重建结果Fig．4 Image reconstruction from PCETs based on the proposed polar method

K为10～100时，重建图像的峰值信噪比(PSNR)如图5所示．由图5可见，K较小时(K＜60)，基于笛卡尔坐标的PCET重建图像与基于极坐标的PCET重建图像的质量相类似，重建图像的PSNR随着K增大而稳步增长．总体来说，基于极坐标的PCET重建图像的PSNR要高约0．4dB．但当K较大时，基于极坐标的PCET重建图像质量明显高于基于笛卡尔坐标的PCET重建图像．基于极坐标的PCET重建图像质量随K单调递增．而在基于笛卡尔坐标的PCET重建图像中，当K增大到某一点(大约为60时)，图像质量达到最大值．当K＞60时，随着K值的增大，图像质量下降．这是因为重建误差(包括几何和数值积分误差)随着K的增加而增大，并在某些时候超过了因增加PCET矩而带来的重建图像质量增益．

图5 PCET重建结果的PSNRFig．5 PSNR of image reconstruction from PCETs

3．2 极坐标下计算PCET的旋转和缩放不变性

对256×256的Lena图像进行以下变换后分析不变性:(1)对图像进行旋转，旋转角度分别为5°、30°、60°、120°、135°;(2)对图像进行缩放，缩放因子分别为 300%、200%、150%、120%、90% 和 75%;(3)对图像进行旋转和缩放，先对图像旋转30°，然后缩放120%．

对上述图像及原图分别在极坐标和笛卡尔坐标系下计算PCET基于极坐标的原图的PCET矩与不同变换类型的PCET矩平均如图6所示．由图6可见，变换后图像的PCET矩与原图的PCET矩基本重合，说明基于极坐标的PCET具有很好的旋转和缩放不变性．

变换后图像PCET矩与原始图像PCET矩的误差如图7所示．由图7可见，基于极坐标的PCET矩比基于笛卡尔坐标的PCET矩具有更好的缩放、旋转不变性．

图6 文中的极坐标下PCET的旋转和缩放不变性Fig．6 Rotation and scale invariance of PCET moments based on the proposed polar method

图7 极坐标与笛卡尔坐标PCET的旋转和缩放不变性Fig．7 Rotation and scale invariance of PCET moments based on Cartesian method and proposed polar method

3．3 速度和存储空间分析

基于极坐标的PCET快速计算方法，其速度提高的原因在于:(1)减少了三角函数和复数运算的次数;(2)利用查找表提高了速度．用Yap等［8］的方法直接在笛卡尔坐标下计算PCET，为8个点生成内核系数需要计算32次三角函数，16次复数加法，在极坐标中用式(11)-(14)直接计算PCET，为8个点生成内核系数需要计算64次三角函数、16次复数加法、8次复数乘法．在文中的快速算法中，为8个对称点生成内核系数需要计算2次复数加法、1次复数乘法，三角函数的计算转换成了查找表的方式，因此计算速度比上述两种方法直接计算PCET有很大提高．文中使用不同分辨率和内容的图像进行实验，图8给出了在PC环境(英特尔2．13 GHz的，2 G内存)，K=10，20，…，100时3种方法的计算时间，算法实现采用Matlab 7．0．从图中可见:文中提出的快速算法的计算时间相比于直接的笛卡尔坐标和直接的极坐标下的计算时间都明显减少;计算速度比笛卡尔坐标的PCET计算方法快6倍以上;随着K增大，计算速度提高越明显．这主要是文中算法计算PCET内核系数时利用查找表，无论K增加多大，计算时间都不会快速增加．

图8 PCET的计算时间比较Fig．8 Comparison of computation time for PCET

4 结语

文中将以极坐标取代笛卡尔坐标计算Zernike矩的方法推广到PHT矩的计算中，提出在极坐标下具有缩放旋转不变的PHT矩计算方法，并对极坐标进行设计和规划，以消除笛卡尔坐标下PHT矩计算中存在的几何误差和积分近似误差．为了提高运算速度，在计算过程中利用三角函数的对称性等相关性质减少三角函数的计算次数，并利用查找表的方式计算矩值，进一步提高计算速度的同时消除迭代累计误差，提高图像的重建精度．文中还通过实验对提出的PCET方法进行了验证，结果表明，该方法在重建精度和不变性上都优于笛卡尔坐标的PCET计算方法，计算速度比笛卡尔坐标的PCET计算方法快6倍以上．提出的快速算法可以推广到PCT和PST的计算中．

［1］Liao S，Pawlak M．On the accuracy of Zernike moments for image analysis［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，1998，20(12):1358-1364．

［2］Xin Y，Liao S，Pawlak M．Circularly orthogonal moments for geometrically robust image watermarking［J］．Pattern Recognition，2007，40(12):3740-3752．

［3］Gao Xinbo，Wang Qian，Li Xuelong，et al．Zernike-moment-based image super resolution［J］．IEEE Transactions on Image Processing，2011，20(10):2738-2747．

［4］Revaud J，Lavoue G，Baskurt A．Improving Zernike moments comparison for optimal similarity and rotation angle retrieval［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，31(4):627-636．

［5］Li S，Lee M C，Pun C M．Complex Zernike moments features for shape-based image retrieval［J］．IEEE Transactions on Systems，Man and Cybernetics(Part A):Systems and Humans，2009，39(1):227-237．

［6］Chen Z，Sun S K．A Zernike moment phase-based descriptor for local image representation and matching［J］．IEEE Transactions on Image Processing，2010，9(1):205-219．

［7］Singh C，Walia E，Mittal N．Rotation invariant complex Zernike moments features and their applications to human face and character recognition［J］．IET Computer Vision，2011，5(5):255-265．

［8］Xin Y，Pawlak M，Liao S．Accurate computation of Zernike moments in polar coordinates［J］．IEEE Transactions on Image Processing，2007，16(2):581-587．

［9］Singh C，Walia E．Computation of Zernike moments in improved polar configuration ［J］．IET Image Processing，2009，3(4):217-227．

［10］Yap P，Jiang X，Kot A C．Two-dimensional polar harmonic transforms forinvariantimagerepresentation ［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence 2010，32(7):1260-1270．

［11］Yang Zhuo，Kamata S．Fast polar harmonic transforms［C］∥2010 11th International Conference on Control Automation Robotics＆ Vision(ICARCV)．Singapore:IEEE Press，2010:673-677．