连续刚构桥0号块水化热温度场分析

朱 波，龚清盛，周水兴

(1.重庆交通大学土木建筑学院，重庆400074;2.重庆市巫山县交通局，重庆巫山404700)

连续刚构桥0号块体积普遍较大，具有明显大体积混凝土特征。0号块作为主要受力部位，其受力状态好坏直接影响全桥安全性和耐久性。在实际中零号块常常存在开裂现象，混凝土水化热产生的温度应力是导致早期开裂的主要原因。

结合水口大桥工程，根据实测环境大气温度、浇筑初温等条件，以ANSYS生死单元模拟混凝土分层浇筑，按瞬态求解方法计算得0号块水化热温度场，理论计算结果与实测数据比较，两者吻合良好。计算发现，浇筑初温对温度场影响呈线性，水化热系数既影响温度峰值，又影响峰值出现时间。

1 热分析有限元计算原理

1.1 热传导方程

混凝土浇筑完成后，可视为具有瞬态温度场的连续均匀介质，水泥水化热作用则可视为混凝土内部热源，其瞬态温度场的计算实质是三维非稳态导热方程在特定边界条件和初始条件的求解。浇筑后具有内部热源的箱梁瞬态温度场热传导方程为［4-5］:

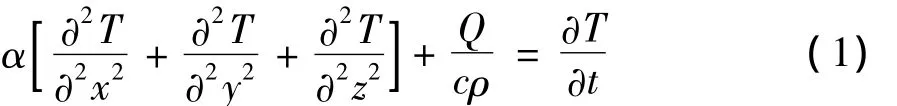
式中:α为导温系数，m2/h;T为混凝土的瞬间温度，℃;Q为热源密度，kg/m3;c为混凝土的比热，kJ/(kg·℃);ρ为混凝土的密度，kg/m3。

由于水化热作用，在绝热条件下混凝土的温度上升速度为:

式中:θ为混凝土的绝热温升，℃;W为单位体积内的水泥用量，kg/m3;q为单位重量水泥在单位时间内放出的水化热，kJ/(kg·h)。

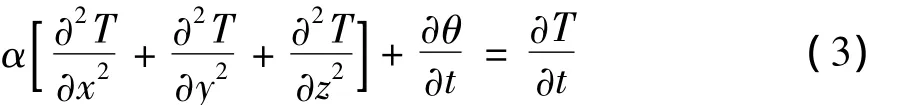
由式(2)，热传导方程可改写为:热源强度q可由累积水化热公式Q(t)=Q0(1-e-mt)求得，即:

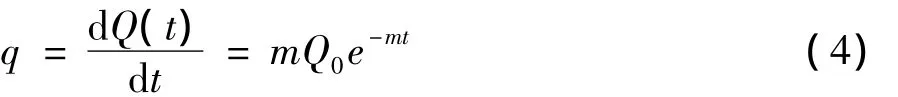
式中:Q(t)为龄期τ时的累积水化热，kJ/kg;Q0为t→∞时的最终水化热，kJ/kg;t为混凝土龄期，d;m为常数，随水泥品种、比表面及浇筑温度不同而不同。

1.2 边界条件

为求解热传导微分方程，还必须知道初始条件和边界条件。对于混凝土水化热温度场分析，初始条件即为在初始瞬时物体内部的温度分布规律。边界条件为混凝土表面与周围介质之间温度相互作用的规律。由于研究的是箱梁外部空气对流热交换边界，即当混凝土与空气接触时，经过混凝土表面的热流量与混凝土表面温度T和气温T0之差成正比［4-5］:

式中:λ为混凝土的导热系数，kJ/(m·h·℃);T0为外界的环境温度，℃;β为表面放热系数，当β趋于无限时，T=T0;当 β=0时，即转化为绝热条件。

1.3 水化热微分方程求解递推公式

当前温度向量{Tn}假设已知，可以是初始温度或由前面求解得到。定义下一时间点温度向量为:

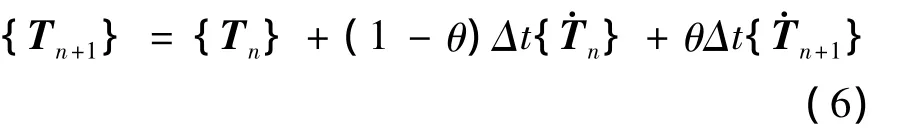
式中:θ为欧拉常数;Δt为计算时间间隔，即步长。

根据式(3)及有限元原理，可得温度场有限元求解方程:

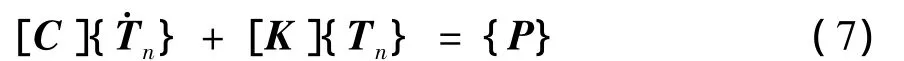
式中:［C］为热熔矩阵;［K］为热传导矩阵;{P}为温度荷载列向量。

根据式(7)有:

将式(8)、式(9)带入式(6)可得瞬态温度场计算递推公式:

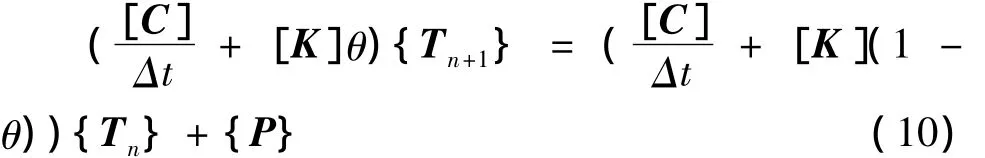
对于混凝土水化热分析，浇筑初始温度为常值。从式(10)可看出初始温度T0对其之后各时间点水化热瞬态温度场Tn影响呈线性，即浇筑初始温度T0改变多少，则各时间点上整个温度场Tn便改变多少。

2 实例

2.1 工程概况

巫山县水口大桥是跨度为50 m+90 m+50 m的连续刚构桥。0号块长11 m，梁高5.5 m，宽为8 m，底板厚1 m，腹板厚1 m，顶板厚0.5 m，横隔板厚1 m，0号块底板中部有一直径为1 m的人洞。梁混凝土为C50，采用华新牌P.0 52.5型普通硅酸盐水泥，每立方米混凝土的材料用量为水泥470 kg，砂650 kg，石子 1 130 kg，水 183 kg，减水剂 7.1 kg。

在大桥0号块施工浇筑工程中进行了温度测试。选择4个截面共布置6个温度测点，1～4点属于第一层，5～6点属于第2层，如图1。

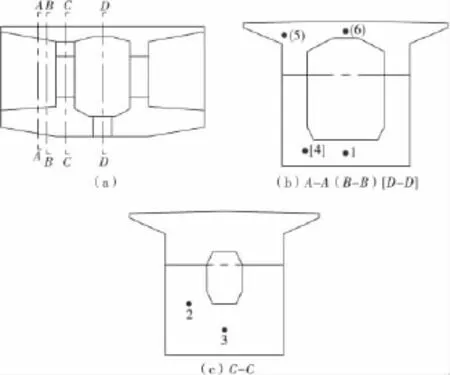
图1 温度测点位置示意Fig.1 Thermal measuring points of sections

2.2 有限元模型

根据0号块箱梁结构对称性，应用通用有限元软件ANSYS建立0号块1/4模型，如图2。模型共划分为11 856个单元、11 953个节点。根据施工方案，零号块分2层浇筑，第1层浇筑高3.5 m，第2层浇筑高2 m，利用ANSYS三维实体温度单元solid70进行施工过程的瞬态温度分析。

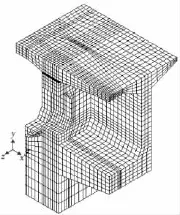
图2 三维有限元模型Fig.2 The mesh division of 1/4 zero block

2.3 边界条件与材料参数

现场实测混凝土入模温度为30℃，箱外大气温度根据监测数据1～20 d内拟合为三角函数:

T=26.326 1-1.376 1cos(- π +2πd)+8.198 3 sin(-π +2πd)(6)

箱内大气温度在1～9 d与箱外大气温度一致，在9～20 d时由于浇筑第2层混凝土内部大气温度先升后降，变化曲线如图3。混凝土表面模板为钢模，箱梁等效对流系数［4-6］外表取 β =75 kJ/(m2·h·℃)、内表面取 β =70 kJ/(m2·h·℃)。

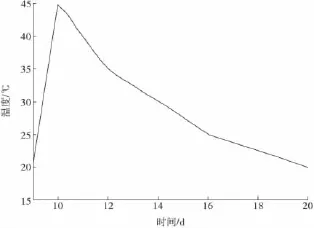
图3 9～20 d箱梁内部大气温度变化曲线Fig.3 The curve of box beam’s internal air temperature in 9～20 days

单位质量水泥最终水化热 Q0=350 kJ［4-6］;单位体积混凝土水泥用量为W=470 kg;水化热系数m=2［4-6］;混凝土密度 ρ=2 450 kg/m3;混凝土热传导系数α 一般为8.39 ～12.36 kJ/(m·h·℃)［1-8］，在此取 α=10.17 kJ/(m·h·℃);比热 c一般为 0.84 ～1.09 kJ/(kg·℃)［1-8］，取 c=1.076 kJ/(kg·℃)。

2.4 实测数据与理论数据对比

计算了0号块在20 d内温度场，计算子步大小为0.05 d。采用ANSYS中生死单元来模拟混凝土分2层浇筑。测量并记录了1、2层混凝土浇筑后5d内实际温度值。图4为实测数据与计算结果比较。

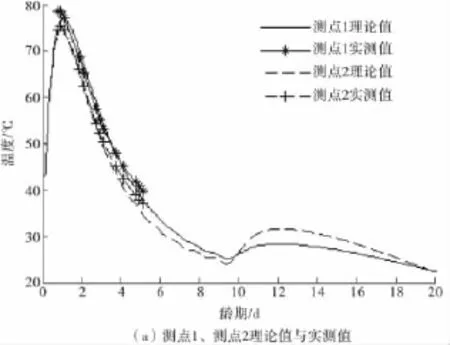
图4 截面各测点实测温度与理论温度对比Fig.4 Comparison of measuring point’s temperatures between measure values and theoretical values

从图4可知:

1)第1、2层混凝土水化热发展趋势理论值与实测值一致，且水化热峰值出现时间、大小大致相同，说明应用有限元方法较好地模拟了混凝土水化热过程。

2)从图4(a)可见第1层测点1～4实测值与理论值比较接近，实测数据与理论值相差均在3℃以内;图4(b)中第2层测点5、6实测值与理论值误差较第1层大，可能是传感器埋置位置偏差所致。

3)当水化热温度趋于大气温度时，实测值与理论值偏差存在增大趋势，分析认为是由于计算边界条件与实际边界条件不一致所致，如拆模后对流边界条件改变等原因。

4)第9 d时浇筑第2层混凝土，第2层混凝土水化热作用对外散发热量，箱内温度逐渐升高，导致第1层混凝土对外散热速率减少，且这时第1层混凝土水化热作用继续产生少量热量，所以第1层混凝土在第9 d后又出现另一温度峰值。

2.5 水化热系数m取值分析

大体混凝土中水泥水化热是影响瞬态温度场最主要因素，水化热系数m决定了水化热速率的大小，而不同水泥品种和浇筑条件又对m取值影响较大。由式(4)可计算得m取不同值时，水化热速率随时间的变化情况，如图5。

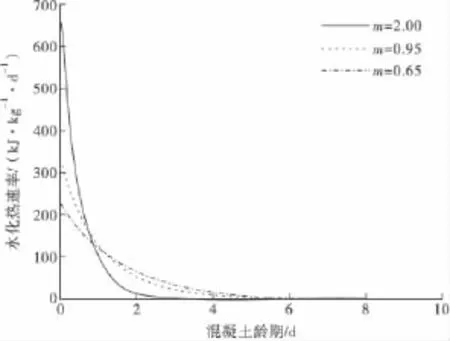
图5 混凝土水化热速率随时间变化曲线(Q0=350 kJ/kg)Fig.5 Concrete hydration heat rate versus time curve(Q0=350 kJ/kg)

从图5可知，m取值越大，混凝土早期水化热速率越高，后期速率衰减也越快，当m=2，在第2 d时，水化热速率几乎为0。混凝土水化热产生的总热量不变，当m值越大，早期水化热速率越高，且衰减也越快，则温度峰值出现时间越早;达到温度峰值时间越短，混凝土对外界耗散的热量就越少，则出现的温度峰值将越大。

3 结语

计算表明，根据瞬态温度场微分方程和有限元程序能够较好地模拟连续钢构桥0号块水化热过程。由微分方程求解递推公式，可知浇筑初温与水化热温度场呈线性关系。水化热系数m同时影响水化热温度峰值和峰值出现时间，m越大温度峰值越大，峰值出现时间越早;对于比较重要的大体积混凝土结构，应根据实际配合比及施工条件，通过实验确定其大小，再将其引入模型中计算。

［1］王新刚，高洪生，闻宝联.ANSYS计算大体积混凝土温度场的关键技术［J］.中国港湾建设，2009，2(1):41-44.Wang Xingang，Gao Haisheng，Wen Baolian.Key technologies for calculation of the mass concrete temperature field with ANSYS［J］.China Harbour Engineering，2009，2(1):41-44.

［2］关战伟.基于ANSYS平台增量法求解大体积混凝土早期弹性徐变温度应力［J］.水科学与工程技术，2008，(增刊1):83-85.Guan Zhanwei.The addition method base on ANSYS to analyse the elastic creep thermal stress of big size concrete building［J］.Water Sciences and Engineering Technology，2008，(Supp1):83-85.

［3］缪长清，孙传志，李爱群.混凝土箱梁桥零号块水化热过程分析研究［J］.防灾减灾工程学报，2010，30(4):407-413.Miao Changqing，Sun Chuanzhi，Li Aiqun.Analysis of hydration heat for block number zero of reinforced concrete beam bridge［J］.Journal of Disaster Prevention and Mitigation Engineering，2010，30(4):407-413.

［4］朱伯芳.大体积混凝土温度应力与温度控制［M］.北京:水利水电出版社，1999.

［5］朱伯芳.水工混凝土结构的温度应力与温度控制［M］.北京:水利水电出版社，1976.

［6］刘兴法.混凝土结构的温度应力分析［M］.北京:人民交通出版社，1991.

［7］朱伯芳.考虑温度影响的混凝土绝热温升表达式［J］.水利发电学报，2003(2):69-73.Zhu Bofang.A method for computing the adiabatic temperature rise of concrete considering the effect of the temperature of concrete［J］.Journal of Hydroelectric Engineering，2003(2):69-73.

［8］张刚，任伟，贺拴海，等.箱梁水化热温度场时效模式及时变应力场［J］.长安大学学报:自然科学版，2008，28(4):51-56.Zhang Gang，Ren Wei，He Shuanhai，et al.Time dependent effect on hydration heat temperature and stress field for concerte box girder［J］.Journal of Chang’an University:Natural Science，2008，28(4):51-56.