舰船过驳6自由度波浪补偿机器人仿真研究

温兆麟，陈爱国

(广州航海高等专科学校船舶工程学院，广东广州510725)

舰船在风浪的作用下存在6个自由度的不规则运动:横摇、纵摇、艏摇、横荡、纵荡和垂荡。舰船在3级以上海况时不能进行安全过驳［1］，而目前研究的舰船过驳波浪补偿机构仅能实现垂荡一个自由度的补偿。为进一步拓展舰船过驳波浪补偿机构的环境适应性，在对基于加速度计阵列的舰船波浪运动数据采集原理和加速度数据检测与积分试验进行研究的基础上［2］，研究了能实现6个自由度波浪补偿的机器人技术，这对新型主动式舰船过驳波浪补偿装置的研发具有重要意义。

1 舰船过驳6自由度波浪补偿机器人建模

为进行船舶6个自由度的波浪运动补偿，设计了六自由度并联机器人机构(图1)。该机构的上平台为静平台，与起重机的减摇吊具相连;可作6个自由度运动的下平台与重物相连;上下平台各通过6个球铰或万向铰与6条支链相链;每条支链的中部为可伸缩的液压缸;上下平台以6个球铰为顶点形成2个内结于半径分别为r和R的圆的凸多边形，分别以上下平台的中点为原点，以过A5A6或B5B6的中点建立x轴，垂直上平台向上建立z轴，按右手规则建立y轴，形成上下两个平台的连体坐标系［3］。

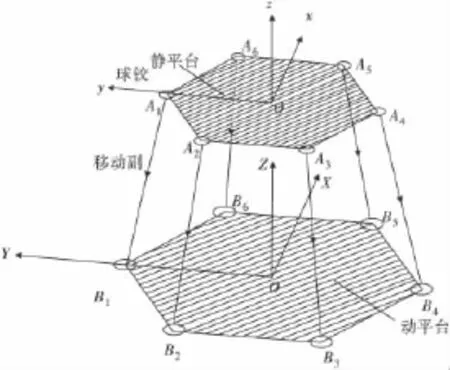
图1 6自由度并联机器人Fig.1 Six-degree-of-freedom parallel robot

设从静坐标系到动坐标系的姿态变换方式为O绕坐标系O-XYZ中的X轴、Y轴、Z轴的旋转角度分别为 α、β、γ，则得到方向余弦矩阵［4-5］:

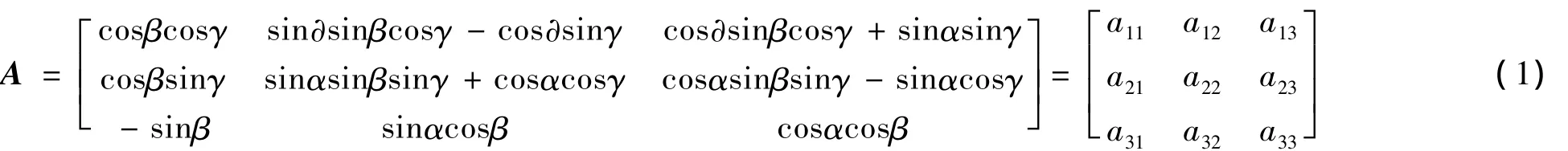
支链在静坐标系中的矢量Li为:

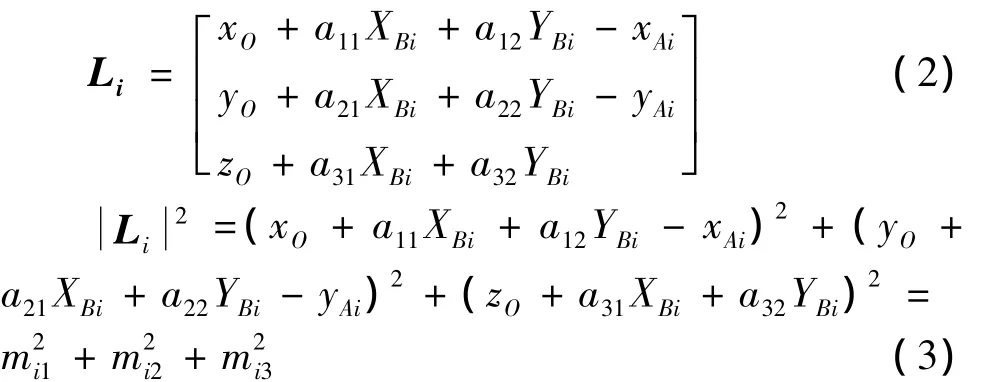
式中:t=［xOyOzO］T是动坐标系原点O在静坐标系中的矢量表示。

6自由度并联机器人的运动学关系为:

式中:

式中:动平台的平移速度为:

动平台在静坐标系中的角速度为:

2 舰船过驳波浪补偿机器人优化设计

针对文中采用的6自由度并联机器人，上下平台均采用长短边相接的方式，而且上平台的短边与下平台的长边相对应用支链相链。令短边所对应的中心角为θ，则长边所对应的中心角为(120-θ)，设静平台连体坐标系的x轴垂直通过长边的中心，如图2，则动静平台各顶点在各自的连体坐标系上的坐标为:

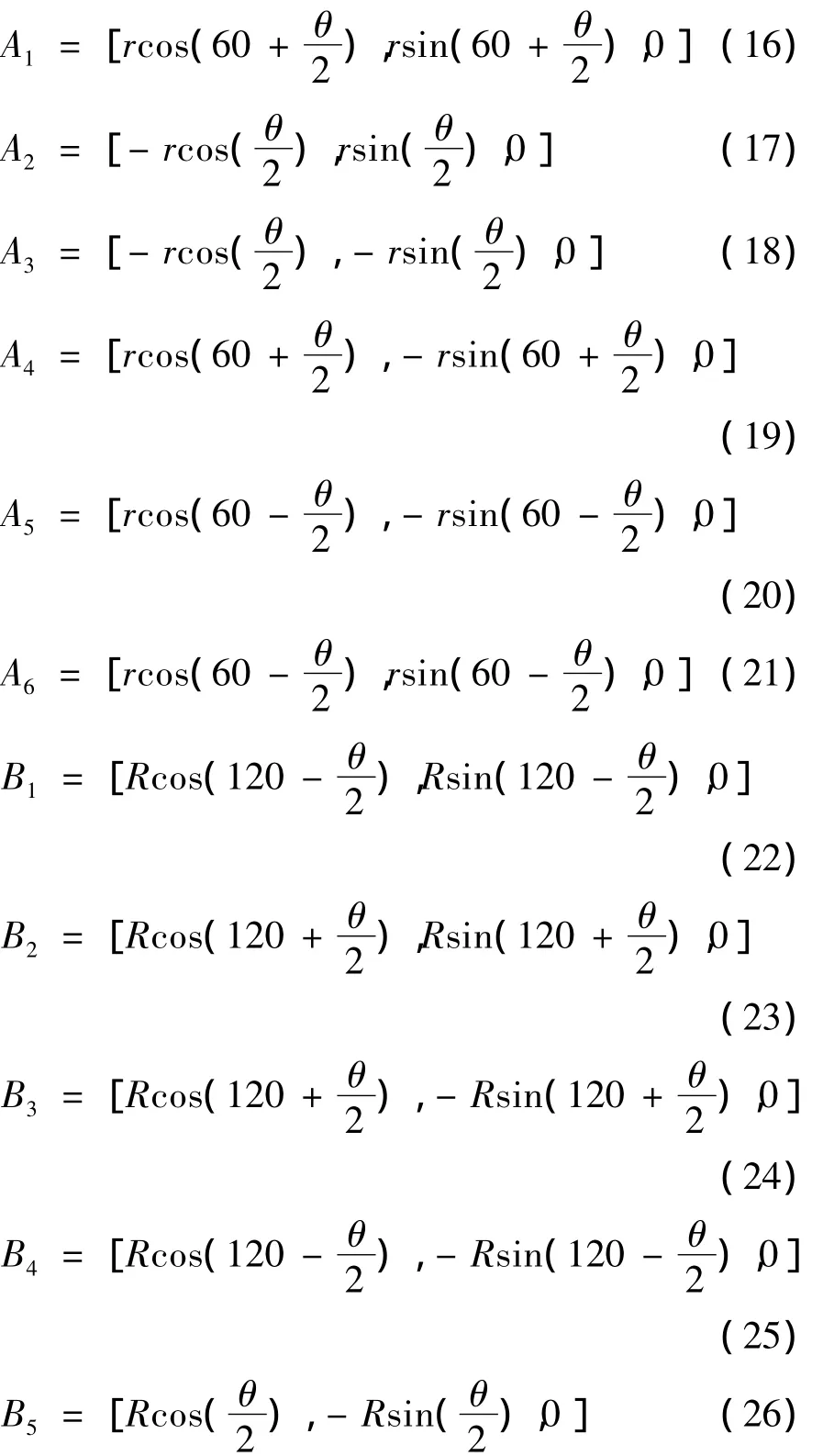
图2 6自由度并联机器人平台坐标示意Fig.2 Platform coordinate of six-degree-of-freedom parallel robot

令短边所对应的中心角θ=36°，静平台半径r=0.8 m，动平台半径等于R=0.64 m，要求动平台在3个方向的平移量可同时达到±0.7 m，编程优化计算得支链最小长度为 1.831 4 m，最大长度为3.462 2 m。机器人补偿前所有支链的初始位置处在2.522 7 m长度处，此时动平台与静平台平行且中心在静坐标系中的坐标为(0，0，-2.5)m。当平台在3个方向的平移量不超过±0.4 m，绕3轴转动的角度至少可同时达±18°，单独绕x轴或y轴转动可达±26°;当平台在3个方向的平移量不超过±0.2 m，绕3轴转动的角度至少可同时达±35°［7-8］。

对于平台的运动传递特性如式(5)所示主要取决于与平台所处位置有关的雅可比矩阵，比如当位置 t=［xOyOzO］T=［0.2，0.2，-0.2］，姿态 α、γ 均为25°，β为-25°，计算得到的矩陈A、B和雅可比矩阵J如式(28)～式(30)。

设3 方向平移速度分别为0.1，0.1，0.2 m/s，3 个角速度分量分别为4.130 8，0.280 5，0.309 5(°)/s，经计算得到此时各支链油杆的速度:

从前面的推导过程可知，向量˙L中的各分量表示的是各油杆长度的变化速率，是无方向的标量，负号表示油杆收缩，平台上行，单位为m/s。

3 舰船过驳波浪补偿机器人仿真实验

设6自由度波浪补偿机器人进行波浪补偿时，动平台中心点O在静平台坐标系中的运动规律为:

以采样时间0.1 s进行离散化抽样。仿真软件流程处理框图如图3。经编程处理得到，仿真船舶过驳波浪补偿系统动平台中心点坐标变化如图4。仿真船舶过驳波浪补偿系统动平台姿态角变化如图5。仿真船舶过驳波浪补偿系统支链长度变化如图6。仿真船舶过驳波浪补偿系统支链速率变化如图7［9］。

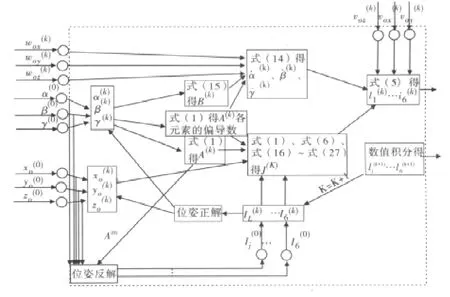
图3 船舶过驳波浪补偿系统仿真软件流程Fig.3 Flaw diagram of simulative soft for compensating wave movement of sealift ships

图4 仿真船舶过驳波浪补偿系统动平台中心点坐标变化Fig.4 Coordinate curve of active platform center point based on simulative soft

图5 仿真船舶过驳波浪补偿系统动平台姿态角变化Fig.5 Pose angle curve of active platform based on simulative soft

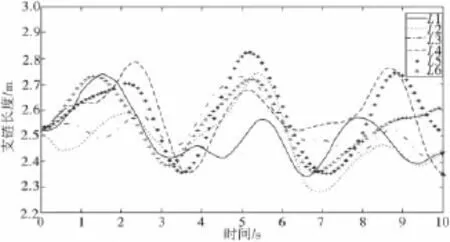
图6 仿真船舶过驳波浪补偿系统支链长度变化Fig.6 Variation curve of branch chain length based on simulative soft

图7 仿真船舶过驳波浪补偿系统支链速率变化Fig.7 Variation curve of branch chain velocity based on simulative soft

4 结语

笔者提出了一种对舰船过驳进行6自由度波浪补偿的机器人，当该机器人在3个方向的平移补偿量不超过±0.4 m，绕3轴转动补偿的角度至少可同时达±18°，单独绕x轴或y轴转动补偿可达±26°;当该机器人在3个方向的平移补偿量不超过±0.2 m，绕3轴转动补偿的角度至少可同时达±35°。该机器人的采用，为舰船过驳波浪运动实现6个自由度的完全补偿提供了可能。

［1］陈远明.舰(船)载直升机平台升沉补偿系统的试验研究［D］.广州:华南理工大学，2007:34-43.

［2］陈爱国，叶家玮，陈远明.基于加速度计阵列的舰船波浪运动检测［J］.深圳大学学报:理工版，2010，27(3):374-378.Chen Aiguo，Ye Jiawei，Chen Yuanming.Measurement principle of ship wave movement based on accelerometer array ［J］.Jornal of Shenzhen University:Science and Engineering，2010，27(3):374-378.

［3］郝轶宁，王军政，汪首坤.六自由度运动姿态模拟系统的研究［J］.北京理工大学学报，2002，22(3):331-335.Hao Yining，Wang Junzheng，Wang Shoukun.A study on a sixdegree-of-freedom platform ［J］.Journal of Beijing Institute of Technology，2002，22(3):331-335.

［4］Chen Aiguo，Ye Jiawe.Research on the genetic neural network for the computation of ship resistance［C］//Proceedings of 2009 International Conference on Computational Intelligence and Natural Computing.Wuhan:IEEE Computer Society，2009:366-369.

［5］Chen Aiguo，Ye Jiawe.Research on four layer back propagation neural network for the computation of ship resistance［C］.Proceedings of 2009 IEEE International Conference on Mechatronics and Automation.Changchun:IEEE Robotics and Automation Society，2009:2537-2541.

［6］李庆扬.数值分析［M］.北京:清华大学出版社，2006:92-100.

［7］吕崇耀，熊有伦.6-6并联机构封闭运动学位姿正解单解［J］.华中理工大学学报，1999，27(7):36-38.Lv Chongyao，Xong Youlun.A closed-form forward kinematics of 6-6stewart in-parallel mechanisms［J］.Journal of Huazhong University of Science ＆ Technology，1999，27(7):36-38.

［8］Ye Jiawei，Chen Yuanming，Wang Dongjiao，et al.Wave motion compensation scheme and its model tests for the salvage of an ancient sunken boat［J］.China Ocean Engineering，2006，20(4):635-643.

［9］解本铭，江训忠.基于ADAMS和MATLAB的三自由度并联打磨机构的运动学仿真［J］.制造技术与机床，2010(8):12-16.Xie Benming，Jiang Xunzhong.Kinematics simulation of 3-D of parallel barinder based on ADAMS and MATLAB［J］.Manufacturing Technology＆ Machine Tool，2010(8):12-16.