傅里叶级数的起源、发展与启示

邓新蒲，吴 京

(国防科技大学电子科学与工程学院，湖南长沙 410073)

在无法进行理论证明时，采用直观推断的研究方法在早期的科学研究中已被广泛采用［1］。由此带来了许多重要的发现，傅里叶级数就是其中之一。

傅里叶(H.Fourier，1768-1830)在研究热传导方程时继承了前人研究天文理论和弦振动方程的方法，直观地断定每一个周期函数都可表示为三角级数，但他并没有给出一个函数可以展开为三角级数的条件，也没有给出严格的证明。尽管如此，傅里叶将Euler(欧拉，1707-1783)等人在一些特殊情形下应用的三角级数方法发展为内容丰富的一般理论，从而开创了数学物理学一个时代。

1 傅里叶级数的起源

1753年，D.Bernoulli(伯努利，1700-1782)提出了采用三角级数解弦振动方程的方法［2］。1759年，Lagrange(拉格朗日，1736-1813)在给 d'Alembert(达朗贝尔，1717-1783)的信中称x2/3可表示为三角级数［3］。1777 年，Euler在研究天文问题时得到［3］

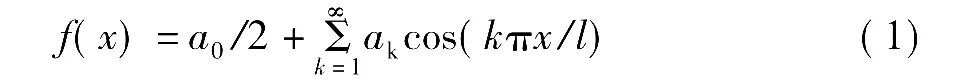
并应用了关系式:

(1)除了因缺少正弦项而只能表示周期为l的偶函数，Euler得到的三角级数与今天我们使用的傅里叶级数已经没有区别。

(2)Euler推出级数系数的方法运用了三角函数的正交性，这正是现在“信号与系统”课程在推导傅里叶系数公式时所采用的方法。

尽管Euler已经得到了类似傅里叶级数的表达式，他所采用的推导级数系数的方法我们今天仍在使用。然而，他与Lagrange及d'Alembert却始终坚持这样的观点:并非是任意的周期函数都可以表示为三角级数。

十九世纪，傅里叶迈出了重要的一步。傅里叶像他同时代的科学家一样，也从事热传导的研究。他在解如下偏微分方程:

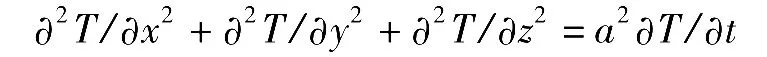
时得到，初始条件 T(x，0)=f(x)必须有［3］

于是，傅里叶面临这样的问题:f(x)能表示成三角级数吗?特别是bk能确定吗?

不妨取l=π，上式简化为

傅里叶把等式左边f(x)和右边的sin kx展开为幂级数，经过并不严格的推导得到

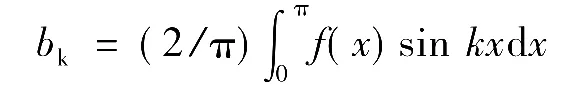
然而，这个结论却不为当时大多数科学家接受，傅里叶仍坚信自己的结论。随后他得到了更精确的结论，即对于任意周期函数，在周期区间(-π，π)上都可以表示为

傅里叶从没有给出“任意”函数可以这样表示的一个完全的证明，也没有说出一个函数可以展开为三角级数所必须满足的条件，但他对此是坚信的。1807年，傅里叶提交的论文被巴黎科学院拒绝了，论文评委之一的Lagrange坚决否认任意周期函数都可以展开为三角级数，并批评了该论文缺乏严密性。事实上，傅里叶始终没有能在他的论文中对傅里叶级数理论做出严格的证明。经过15年的抗争，直到Lagrange离世9年后的1822年，他终于出版了专著《热的解析理论》，直到此时人们才勉强地承认了他的思想。

我们可以列出傅里叶在方法上存在的缺陷。比如傅里叶在求级数系数时采用的方法不够严密，并且比Euler所采用的运用三角函数正交性质的方法要复杂得多。尽管存在一些缺陷，傅里叶得到了正确的结论。傅里叶的结论展示了强大的生命力，对数学的发展也产生了深远的影响，这是傅里叶本人及其同时代人都难以预料到的，而且这种影响至今还在发展之中。

(1)傅里叶级数促进了偏微分方程理论的发展，成功地解决了关于弦振动问题的解的争论;

(2)傅里叶级数促进了函数概念的发展，傅里叶级数理论的先驱者们认为函数必须由一个解析表达式表示;

(3)傅里叶级数标志着人们从解析函数或可展成Taylor(泰勒，1685-1731)级数的函数中解放出来。Taylor级数仅在函数的解析点附近表示该函数，而傅里叶级数在一整段上表示一个函数。

2 傅里叶级数的严密化

随着数学思想的进步，傅里叶的成就在后来赢得了广泛的赞许。但严格地讲并不是任意周期函数的傅里叶级数都收敛。关于收敛条件和收敛证明问题的研究，后继者 Cauchy(柯西，1789-1857)和Poisson(泊松，1781-1840)的努力没有结果，代表性的成果是 Dirichlet(狄利克雷，1805-1859)和 Riemann(黎曼，1826-1866)做出的［4］。

2.1 Dirichlet条件

Dirichlet在1822年至1825年间在巴黎几次会见傅里叶之后，对傅里叶级数产生了兴趣。1829年他在论文《关于三角级数的收敛性》中给定并证明了:当f(x)满足下列条件时其傅里叶级数是收敛的，这就是Dirichlet条件:

(1)f(x)是单值有界的;

(2)f(x)是分段连续的，即在一个周期内只有有限多个间断点;

(3)f(x)是分段单调的，即在一个周期内只有有限多个极值点。

今天的教科书中，条件(1)已放宽为绝对可积［5，6］，使得工程上所遇到的绝大多数函数都满足Dirichlet条件。条件(2)和(3)排除了无穷间断点和无穷振荡的情形。

Dirichlet迈开了傅里叶级数严密化的坚实的第一步，以致Riemann尊称他为傅里叶级数理论的真正奠基者。关于傅里叶级数收敛性的研究持续到今天有很多结果，但Dirichlet条件在今天“信号与系统”教科书中使用最为广泛。

2.2 Riemann 引理

Riemann曾在Dirichlet指导下研究傅里叶级数。1854年他在论文《用三角级数表示函数》中证明了:如果 f(x)在周期［-π，π］上有界可积，则有

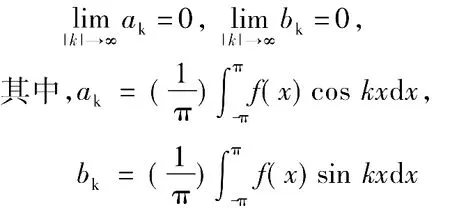
这就是Riemann引理。进一步将定理有界可积条件放宽为 Lebesgue绝对可积(H.Lebesgue，勒贝格，1875－1941)，该定理称为 Riemann-Lebesgue引理。Riemann同时还证明了f(x)在一点的收敛特性只依赖于 f(x)在该点邻域中的特性［4，7］。

Riemann-Lebesgue引理是证明傅里叶级数收敛性的重要工具［7，8］。1880 年 U.Dini(迪尼，1845-1918)给出了另一个傅里叶级数收敛的充分条件:满足 Lipschitz条件(R.Lipschitz，科普希茨，1932-1903)的函数f(x)其傅里叶级数收敛。对该定理的证明就采用了Riemann-Lebesgue引理［8］。

2.3 Gibbs现象与一致收敛

1881年 Jordan条件(约当，C.Jordan，1838-1922)给出了又一个Fourier级数收敛的充分条件:有界变差函数f(x)的Fourier级数收敛于［f(x+0)+f(x－0)］/2。

1898 年，J.Gibbs(吉布斯，1839-1903)发表文章证明了有界变差函数的傅里叶级数在间断点的振荡规律，因此这一现象称为Gibbs现象。这一现象展示了傅里叶级数在间断点收敛的不一致性。

记f(x)的傅里叶级数的部分和为SN(x)，级数在x0收敛的定义为:;级数在周期T上的一致收敛的定义为:关于函数f(x)的傅里叶级数一致收敛的一个充分条件是:f(x)在一个周期上满足一致Lipschitz条件。

2.4 连续函数傅里叶级数的收敛性

在Dirichlet的研究工作之后的约50年间，人们相信任何连续周期函数的傅里叶级数都收敛到该函数。然而在 1873年 P.Reymond(雷蒙德，1831-1889)给出了一个连续函数［9］，其傅里叶级数在一点发散。

1904 年 L.Féjer(费耶，1880-1959)证明了可采用算术平均方法由任何连续周期函数的傅里叶级数(即使该级数发散)重构该函数［4，7，9］，即任何连续周期函数f(x)的傅里叶级数在算术平均和的意义下总是收敛于该函数。记f(x)的傅里叶级数的部分和为SN(x)，上述结论用公式表示总是成立。其中，σN(x)=(1/N)［S0(x)+S1(x)+… +SN－1(x)］。

Reymond指出连续函数的傅里叶级数在某些点发散，而Féjer则证明了级数在算术平均和意义下总是收敛于该函数。关于连续函数的傅里叶级数的收敛问题似乎解决了。然而1926年A.Kolmogorov(柯尔莫果洛夫，1903-1987)证明存在Lebesgue可积的周期函数［9］，它的傅里叶级数处处发散。1966年，J.Kalhane(卡亨，1926-) 和 Y.Katznelson(卡茨纳尔松，1934-)指出在任意给定的零测集上，存在连续周期函数的傅里叶级数在该集合上所有点都发散［9］。关于连续周期函数的傅里叶级数的收敛性似乎又不乐观了。

然而在同一年L.Carleson(卡尔松，1928-)发表文章指出:对于平方可积的周期函数，其傅里叶级数几乎处处收敛［9］。这是一个人们预料之外的好结果，因为连续周期函数在一个周期内是平方可积的。综合Carleson和Katznelson的结果，即连续周期函数的傅里叶级数只在零测集上发散，亦即几乎处处收敛。至此关于连续函数傅里叶级数的收敛性问题就完全清楚了。

3 傅里叶级数的Hilbert空间表述

将周期函数理解为某个线性空间上的矢量，函数的傅里叶级数展开则可理解为该空间上矢量的正交分解。级数展开的这种表述方式使得傅里叶级数的公式推导简明、易于理解。而函数在更多类型的基上的正交分解，就是广义傅里叶级数的思想。

3.1 傅里叶级数的Hilbert空间表述

现设周期函数一个周期为［-π，π］，［-π，π］上平方可积函数集合记为L2［-π，π］。该集合满足线性空间的定义，因而构成线性空间。在此空间上定义内积如下:

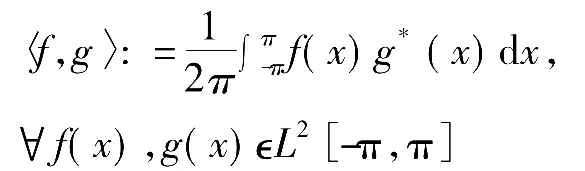
则L2［-π，π］构成完备内积空间，即Hilbert(希尔伯特，1862-1943)空间。函数集 {ek=eikx，k}是该空间中的完备正交基。在此空间上任意函数f(x)的傅里叶级数表示为

上述傅里叶级数的Hilbert空间表述方法是被Euler运用了三角函数正交性质表示三角级数方法的理论上完善，也是当今工科类“信号与系统”教科书中所采用的方法。

Carleson证明了平方可积周期函数的傅里叶级数几乎处处收敛。即对于L2［-π，π］空间上的任意函数 f(x)，记，则有(x)2|dx=0。这一结论在工程上理解为，函数展开为傅里叶级数其能量是保持的。

L2［-π，π］空间上的任意函数 f(x)展开为傅里叶级数，则可得到Parseval(帕赛瓦尔，1755-1836)等式成立

上述公式可解释为，周期信号的平均功率等于直流分量及各次谐波平均功率之和。

由于 {ek=eikx，k}中元素的两两正交性，根据可得

上式即是Parseval等式的另一种形式。将傅里叶级数理解为空间上的正交分解，上式即表示矢量长度平方等于各正交分量长度平方之和，即可理解为勾股定理的推广。

3.2 关于广义傅里叶级数

前面已经指出，类似于几何空间上矢量的正交分解，周期函数的傅氏级数展开是在内积空间上函数的正交分解。其正交分解从 {ek=eikx，k}基推广到Legendre(勒让特，1775-1837)多项式和Haar(哈尔，1885-1993)小波基等，称为广义傅里叶级数［8，9］。

除了Legendre多项式外，还有很多正交多项式，如 Hermite(埃尔米特，1882-1901)多项式、Laguerre(拉盖尔，1834-1886)多项式和 Tchebysheff(切比雪夫，1821-1894)多项式等可构成广义傅里叶级数的正交基。函数在这类基上的级数展开在信号处理中有很多应用。小波分析理论则将Haar小波基进行了进一步推广，因此在这种意义上讲小波理论是傅里叶级数发展的结果。

4 结语

傅里叶级数是“信号与系统”课程的核心，也是处理科学和工程诸多问题不可或缺的理论工具。本文希望通过介绍傅里叶级数的产生和发展过程，带给读者这样一些启示:

(1)尽管科学研究必须是严密的，但是我们必须重视和发挥直觉在科学研究中的作用。傅里叶从热传导方程解的研究中正是凭直觉发现了傅里叶级数，从而开创了数学物理学一个时代。

(2)我们要善于归纳问题之间的联系，发现数学方法的统一性，从而有助于研究工作的创新。从正交分解的意义上，广义傅里叶级数和小波理论正是傅里叶级数理论的统一和发展。

［1］ Lars Garding，胡作玄译.数学概观［M］.北京:科学出版社，2001

［2］ http://acd.ucar.edu/textbook/ch15/Fourier/Fourier.cite1.html

［3］ Morris Kline，朱学贤等译.无穷级数，《古今数学思想》第二册第20章［M］.上海:上海科学技术出版社，2002

［4］ Morris Kline，邓东皋等译.分析中注入严密性，《古今数学思想》第四册第40章［M］.上海:上海科学技术出版社，2002

［5］ M.J.Roberts，Signals and systems［M］.Boston:McGraw Hill Higher Education，2004

［6］ Alan S.Willsky，Signals and systems.MIT open courses，Sept.2003

［7］ 潘文杰.傅里叶分析及其应用［M］.北京:北京大学出版社，2000

［8］ James S.Walker，Fourier series.in“Encyclopedia of Physical Science and Technology”［M］，Salt Lake City:Academic Press，2004

［9］ Pierre Bremaud，Mathematical principles of signal processing-Fourier and wavelet analysis［M］.Newyork:Springer，2001