再谈带电微粒在复合场中的运动问题

魏 强

（屏山县中学校 四川 宜宾 645350）

文献［1］中就部分教师和学生对带电粒子在复合场中运动这一类问题存在的错误理解和认识举了一例，并做了详尽的分析.题目如下.

题目：一电荷量为q的小球固定在与水平面平行的足够大的匀强磁场中，如图1所示.若匀强磁场的磁感应强度为B，小球的质量为m，自由释放后，试分析小球的运动情况并求出其下落的高度.

图1

错解：小球自由释放，在重力作用下开始运动.在运动过程中，小球受到重力和洛伦兹力作用.在这两个力的作用下，重力改变物体的速度大小，洛伦兹力不断改变速度的方向.当小球运动到某一位置的时候，重力和洛伦兹力刚好等大反向时，物体开始做匀速直线运动.则有

又因为小球在运动过程中，洛伦兹力不做功，由机械能守恒定律有

解得

文中作者就定性地对小球运动到最低点的受力情况进行了分析，并指出了小球在最低点处不可能做匀速直线运动.但就此得出此题所给条件不足，不能求出小球在最低点运动的速度和下落高度.笔者不敢苟同.

不妨从微分方程入手来研究这一问题，不但可以定量地得出小球的运动情况，还可以求出小球在最低点运动的速度和下落高度.

正解：以小球下落点为坐标原点建立xOy坐标系，如图2所示.任选小球下落过程中的一点P.根据牛顿第二定律建立小球的运动微分方程

图2

式（1）对时间t积分，得

其中C为常量，根据初始条件，t＝0时

化简为

将（3）式代入（2）式得

该对应齐次方程的通解为

非齐次方程的特解设为

代入（4）式得

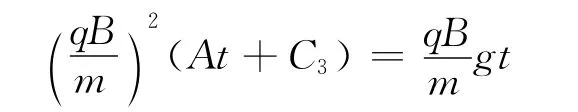
所以

该非齐次方程的通解为

将其对时间求导得

根据初始条件，t＝0时，x＝0，x·＝0得

式（2）对时间t积分得

由初始条件，t＝0时，x·＝0，y＝0得

代入（5）式得

将（6）式代入（1）式得

该齐次方程通解为

非齐次方程的特解设为

代入（7）式得

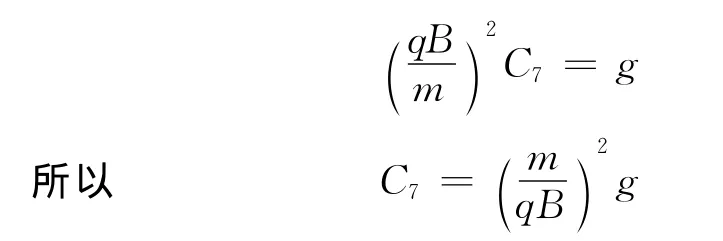
该非齐次方程的通解为

上式求导得

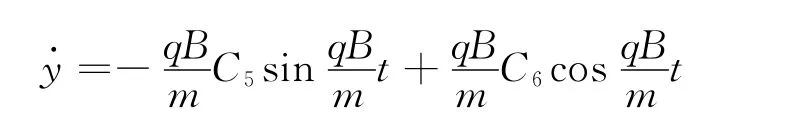
根据初始条件，t＝0时，y·＝0，y＝0得

最后得到了带电小球的运动方程

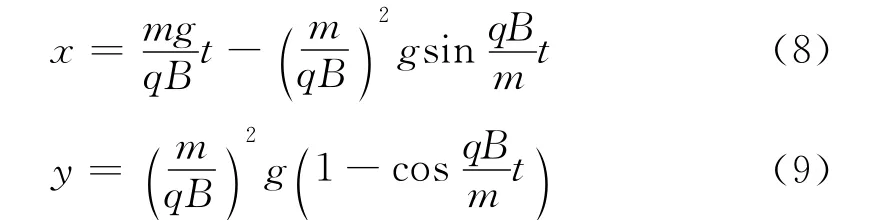
从带电小球的运动方程中，可以看出小球的运动具有周期性的，由数学方法求周期.可从运动方程中得到

将小球的运动方程（8）、（9）式变形可得

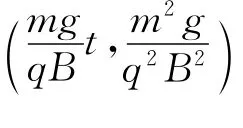
讨论：（1）由小球在y轴上的运动方程为

可知，只有当cosqBt＝－1时，y取最大值，即为m

也?就是小球下落的最大高度.

由＝π得，小球的运动时间为

此时的速度也可用求导的方法求出

速度方向沿x轴方向.

此时的洛伦兹力为f洛＝qv合B＝2mg，方向竖直向上.可见，小球的合力不为零，不可能做匀速直线运动.也可据此求出小球下落的高度

图3

从（8）式与（9）式中消去t可得到轨道方程，根据（8）式与（9）式作t，x，y的数值表后也可得到y与x的函数关系，从而可得到小球的运动轨道如图3所示.

1 胡均宇.关于带电粒子在复合场中运动的题目误解分析.物理通报，2010（3）：43～44