中国宏观经济变量预测的实证研究——以小规模动态因子模型的应用为例

许获迪，于 洋

（1.对外经济贸易大学 国际经济贸易学院，北京 100029；2.国网北京经济技术研究院，北京 100052）

一、引言

动态因子模型（Dynamic Factor Model， DFM）是一种对经济变量的维度进行压缩，提取经济现象背后的“隐性推动因素”进行相关分析和预测的模型（John Geweke，1977），是收缩模型（shrinking methods）中的一种。动态因子模型可提取动态因子作为宏观经济的领先指数和同步指数，从而发展出了“自动领先指数”（Automatic Leading Indicator， ALI）模型，即将提取出的动态因子放入向量自回归（VAR）模型中对经济变量进行预测。

近10年，动态因子模型已经成为使用大量预测变量来预测宏观经济的主要研究框架。这些大规模的动态因子模型一般使用几十个甚至两百多个变量来预测宏观经济序列，研究结果表明，大规模动态因子模型在短期预测方面优于宏观经济计量结构模型（Macroeconometric structural models，MESMs）、ARMA（Auto-Regressive and Moving Average Model）、VAR 等传统的时间序列模型和其他Shrinking Methods［1］。理论上，大规模的DFM能够具有如此的优势主要是因为［2］：通过提取动态因子，DFM能够很好地利用其他模型难以容纳和处理的大规模多维度的信息，这将海量数据从一个软肋变为了优势；但是该理论优势在实践中并未完全得以确认［3］，大规模DFM的预测效果并非总是令人满意。原因可能在于，构造模型时，大规模的动态因子模型更容易引入不合适的变量，涵盖冗余信息和不必要的波动，降低预测的精确度，某些变量的组合甚至导致海塞矩阵非半负定，因此动态因子模型涵盖的变量并非越多越好［4］。另外，大规模动态因子模型运行代价大，对软硬件要求高，甚至33个预测变量以上的动态因子模型在目前通用的Stata等商业软件上无法运行。上述情况在一定程度上使得大规模动态因子模型的应用受到限制。

应用动态因子模型的另一个方向是小规模动态因子模型［5］，即采用3—5个变量，提取一个动态因子来预测目标序列，这类研究也取得了很好的预测效果。相对于大规模DFM，小规模DFM易于调试，运行效率高。可是，小规模动态因子模型和传统的结构模型、时间序列模型一样，仅选取少量变量，选择哪些变量则成为一个问题［6］。目前还没有文献把小规模动态因子模型放到与其他模型对比的情景下，分析和探讨其预测效果和应用前景。

通货膨胀率不论在理论上或实践中都是一个重要的宏观经济变量，也是众多研究在比较宏观经济变量预测效果时通用的标准变量。然而，由于通货膨胀集中体现了国际经济、金融危机等难以预料的冲击，该数据成为公认的难以预测的宏观经济变量之一［2］。本文正是将通货膨胀率作为中国宏观经济变量的代表，采用小规模动态因子模型预测中国通货膨胀，并且就此探讨小规模动态因子模型的一些特性和在实践中的适用性。

二、模型原理与变量

（一）动态因子模型原理

动态因子模型从若干变量中提取潜在的、观察不到的共同趋势，并利用这个共同趋势，即动态因子，对经济变量进行预测。目前，动态因子模型广泛应用于预测美国、英国和欧洲的宏观经济变量。下面我们首先简要介绍动态因子模型。令

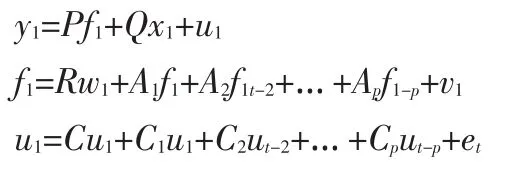
其中，yt是内生变量组成的k维向量，ft是不可观测的因子组成的n维向量，xt是外生变量组成的矩阵，扰动vt、et独立同分布。在动态因子模型中，内生变量组成的向量受到一些不可观测的因子以及外生变量的影响。不可观测的因子及扰动具有向量自回归的结构。

（二）变量选择

本文的预测目标为通货膨胀率。鉴于消费者价格指数是各国计算通货膨胀率的主要指标，本文选择以消费者价格指数表示的年通货膨胀率为预测变量。

DFM系数据驱动型模型，其解释变量的选取并不受经济理论的严格约束，然而，其变量的选取并不是随意的。首先，DFM是从对数线性化宏观经济结构模型，包括动态随机一般均衡模型中自然演变出来的［2］，参考相关理论和基于理论的MESMs所包含的变量有助于变量选取。在此基础上，应依靠直觉并尝试对变量进行调整，增加更合适的信息或者去除多余的信息，以提取更有解释力的动态因子，达到更好的预测效果。其次，有些变量放在一起时，必有其中之一不显著，甚至导致海塞矩阵非半负定，使得模型不能运行［5］。例如进口和出口，因为它们之间有太强的相关关系，对于这些变量要删除其中一些使其不再有冲突。

依照上述原则，参照Qin的MESMs模型，删去了有冲突的变量，并且通过增删变量试探调整，采用八组变量滤出八个动态因子，每组变量在3—5个之间。这八个因子与该MESMs模型涵盖的八个模块一一对应。选择参考Qin的模型作为参照的原因是：Qin在另一篇文章中提供了该MESMs模型和在此基础上的ALI模型预测结果，可与本文的结果进行对比。

（三）数据来源

本文共选用27个变量，所有变量均选自中经网数据库，数据的样本期为1999年1月至2011年12月。其中，2011年1月至2011年12月的数据用来做样本外预测。该数据包含：（1）月度数据；（2）季度数据；（3）近期数据完整而远期数据有缺失，如“高新技术产品进口额_累计”从2000年1月才开始统计的；（4）在固定观测期缺失变量的数据，如财政方面的数据普遍缺少12月的数值。具体见表1。

变量处理方面，对所有非百分比或比率的数据取自然对数，并对所有宏观实体经济变量采用X-12方法进行季节调整［6］。所有变量都采取年增长率的形式，考虑到动态因子模型主要关注短期预测，直接取增长率即可满足采用状态空间模型进行卡尔曼滤波对变量的平稳性要求，因此略去了变量间长期协整关系带来的修正作用。对于季度数据，为了将其转化为月度数据，我们简单地假设其中每个月的年增长率与该月所处季度的相同，并且，我们参照Stock和Watson的做法，对所有变量都进行了标准化。

表1 变量列表

三、实证分析

本文采用以下步骤来进行实证分析：首先，采用小规模动态因子模型，根据理论和相关MSEMs滤出八个动态因子分别预测中国通货膨胀率，并比较其预测效果。其中，先与大规模的MESMs、ALI和动态因子模型比较；然后进一步与其他采用少量变量的传统预测模型比较，此处选用VAR模型作为传统时间序列模型的代表。其次，尝试对模型进行优化和改进。再次，根据实证结果讨论模型的特性和适用性。

如前所述，依靠理论、直觉和变量间的比较与调整，从数据库中筛选出8组变量，每组变量在3—5个，分别提取一个动态因子来预测中国通货膨胀率。变量和因子之间的对应关系如表2所示：

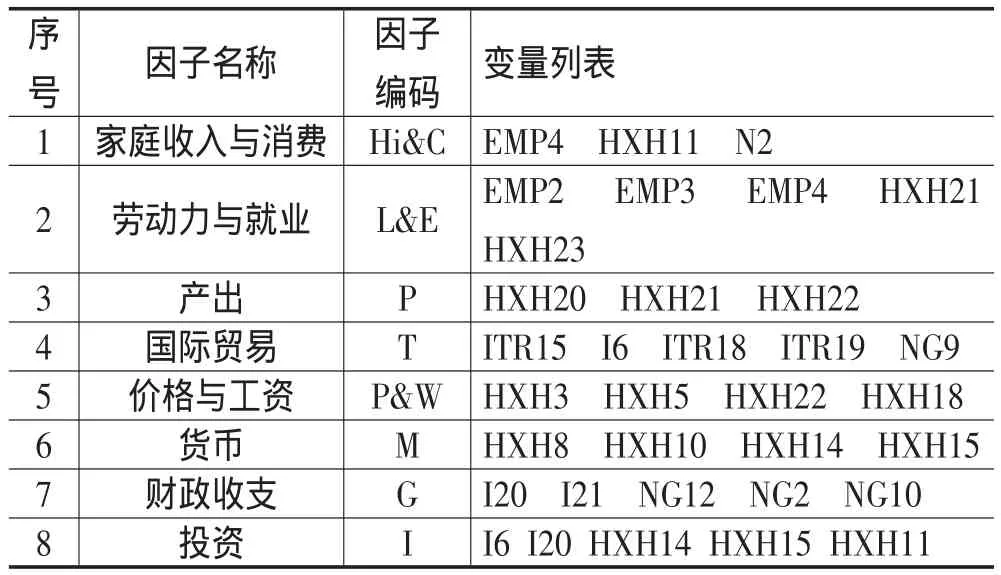
表2 因子与变量的对应关系

为了便于与其他模型比较，首先简单地统一采用p=1，q=2来构建模型，并以此作为下一步优化的基准模型。采用MSE和RMSE来衡量每个单因子模型的样本外一步预测的效果，如表3所示：

表3 单因子动态因子模型对中国通货膨胀率预测结果

可以看出，上述八个单因子模型的预测效果较为接近，RMSE在0.85—0.89之间，MSE在0.72—0.98之间。下面将这个初步的结果与各类大规模模型（MSEMs、ALI和DFM），以及小规模时间序列模型（VAR）比较。

1.对比大规模模型

首先，该结果优于Qin的MSEMs。Qin的同一篇文章还在四种情景中应用ALI模型预测中国的季度通货膨胀率，表3的结果优于其中两种。鉴于季度预测的效果普遍优于月度预测，并且Qin的研究还采取了引入ECM项等一系列优化方法，若不考虑这些额外的优化手段，在同一标准下，小规模DFM的预测效果优于20多个变量的普通ALI模型。

不失一般性，再将表3的MSE数值与Stock的超大规模动态因子模型（含200多个变量）的预测结果比较。Stock的研究同样在不同的情景中包含了一系列优化手段，而表3中的结果同样优于其中一半以上的情景，为了简便此处不展开。

大规模的动态因子模型因变量众多，在选择时难以排除变量间的冲突，或者是变量带来的冗余信息；而小规模的则方便控制和调试，从而可以纳入适当的信息量。由此可见，小规模的动态因子模型确实能以较小的变量选择和程序运行代价，获得很好的预测效果。

2.对比小规模模型

下表分别列出了八个单因子的DFM模型（p=1，q=2）和分别采用八组与小规模DFM相同变量的VAR模型（lags=2）预测通货膨胀率的RMSE（见表4）。

表4 单因子动态因子模型和VAR模型的比较

预测结果表明，单因子的动态因子模型预测效果整体优于VAR模型。逐个因子比较，仅有P&W因子的VAR预测效果优于DFM，而且该数值比其他因子的DFM预测都要差，这主要是由于P&W因子自身的特殊性造成的。由后文可知，当P&W因子的DFM预测调整到p=1，q=1时，RMSE为0.88，优于此处的VAR预测。

另外，DFM预测的RMSE较为接近，而八个VAR模型的预测效果则差别较大，RMSE从0.90到1.22。这说明在小数据集的情况下，普通的时间序列模型在变量选择上远比动态因子模型敏感，采用小规模动态因子模型构建更为容易，而且能够获得更稳健、更好的预测效果。这是因为动态因子模型关注经济现象背后的“隐性因子”，使得隐藏在变量背后的共同推动因素得以显现，而摒除了每个变量的冗余信息，因此，该做法明显优于传统的仅采用少量变量直接进行预测的做法。Shrinking Method滤出共同趋势的优势不仅仅显现在大数据集上，该优势在小规模动态因子模型上也体现得十分明显。

［1］杜勇宏，王健，王汝芳.动态因子模型与ARMA模型的比较[J]. 统计与决策，2011，（5）：31—32.

［2］James H.Stock，Mark W.Watson.Generlized Shrinkage methods for forecasting using many predictors[R].EOMMS：JBES09—255，2010.

［3］Eichmeier，Ziegler How successful are dynamic factor models at forecasting output and inflation？ A meta-analytic approach[J].Journal of Forecasting，2008，（3）：237—265.

［4］Marcellino，M.，Stock，J.H.，M.W.Watson.Macroeconomic Forecasting in the Euro Area：Country Specific Versus Euro Wide Information[J].European Economic Review，2003，（47）：75—122.

［5］Geriach， S.，M.S.Yiu.A Dynam ic factor for Current-quarter Estimates pf Economic Activity in Hong Kong[R].HKIMR Working Paper No.16，2004.

［6］何启志，范从来.中国通货膨胀的动态特征研究[J].经济研究，2001，（7）：91—101.