基于自由权矩阵法的网络控制系统稳定性研究

孙坚栋,蒋静坪

（浙江大学 电气工程学院，浙江 杭州310027）

网络控制系统 NCSs（Networked Control Systems）是指通过网络形成闭环的反馈控制系统，其主要特征是系统各功能部件通过网络交换控制信息。与传统点对点结构的控制系统相比，NCSs具有减少电缆使用、降低安装和调试费用、易于维护和故障诊断等诸多优点，应用前景非常广阔，目前已在网络制造、兵器系统、远程医疗、远程故障诊断和试验等复杂控制领域得到了使用[1]。

由于网络带宽的限制,在NCSs中进行信息交换时不可避免地存在传输时延，根据所使用网络协议的不同，时延可能是定常、周期性或随机变化的。此外，网络不是绝对可靠的传输介质，除了时延之外，在NCSs中还存在因节点竞争和信号干扰等因素引起的数据包丢失问题。时延和丢包是导致NCSs性能变差、甚至不稳定的重要原因。

从本质上看，NCSs是一类包含时变、有界输入时延的时滞系统。目前在一般时滞系统的稳定和镇定方面已经取得了大量成果，如还原法、奇异系统法、自由权矩阵法等。其中自由权矩阵法是最有效的方法之一，它的基本原理是利用零等式将多个自由权矩阵引入李雅普诺夫泛函的微分中。使用该方法时一般不需要进行模型变换，因而克服了产生保守性的一个重要根源。

如果把一般时滞系统的研究成果结合网络控制系统的特点加以应用，则可以得到关于NCSs的分析和设计方法。参考文献[2-4]将存在时延和丢包的NCSs建模为具有时变输入时延的连续或离散时间时滞模型，利用自由权矩阵法进行稳定性分析和控制器设计，推导出基于线性矩阵不等式 LMI（Linear Matrix Inequality）的渐近稳定充分条件。上述文献在NCSs建模时同时考虑了时延和丢包的影响，模型接近实际情形，因此具有一定的实用价值，但是它们都舍弃了李雅普诺夫泛函微分或差分中的某些非正交叉项，导致结果具有保守性。另外，网络时延的实际最小值一般大于0，而参考文献[2-4]假设最小值为 0，GAO等人[5]指出，这种处理方式人为地扩大了时延变化范围，也将带来保守性。

本文将包含随机、有界传输时延和丢包的NCSs建模为离散时间时滞模型进行稳定性分析，推导出基于LMI形式的渐近稳定充分条件。不同于参考文献[2-4]，本文在建模时假设时延的最小值不为0，并且在处理李雅普诺夫泛函差分时，采用合理方法消除其中产生的非正交叉项，而不是在同类文献中使用的简单舍弃的做法，降低了系统保守性。

1 网络控制系统的模型

设被控对象的离散时间状态方程为：

式中，x(k)∈Rn为状态向量，u(k)∈Rm为输入向量，A、B为适维常数矩阵。当系统状态全部可测，并采用增益为K的静态反馈控制器时，在传统计算机控制系统中，各部件之间不存在传输时延，有

在 NCSs中，由于存在时延和丢包，式(2)不成立，即kT时刻的输入u(k)一般不是根据kT时刻的状态计算得到的。

典型NCSs的结构如图1所示，其中存在传感器到控制器的时延τsc、控制器计算时延τc以及控制器到执行器的时延τca，τc一般可忽略。另外在NCSs中还存在丢包，图1中dsc表示传感器到控制器的连续丢包数，dca表示控制器到执行器的连续丢包数。

图1 典型网络控制系统的结构

为了建模需要，提出以下关于NCSs的4个假设：

(1)控制数据采用单包传输；

(2)系统状态全部可测并采用状态反馈控制器；

(3)传感器和执行器采用时钟驱动，控制器采用事件驱动；

(4)传输时延和连续丢包数是时变、有界的，其中时延下限可以不为0。

由假设(1)，在反馈或前向通道中传输的数据具有相同的时延和丢包数。由假设(2)，可以将反馈通道和前向通道中的两部分时延合并，得到总时延 τk=τsc+τca。 由于执行器采用时钟驱动，因此是采样周期T的整数倍，定义以T为单位的总时延εk=τk/T。同理，连续丢包数 dsc和dca也可以合并，得到总丢包数dk=dsc+dca。由假设(4)，传输时 延和 丢包数 是有 界的 ，即 εk∈[εm,εM]、dk∈[0,dM]。

由于时延的影响，根据lT时刻状态计算得到的控制量，将在(l+εl)T时刻输入到被控对象。发生丢包时，假设根据lT时刻状态得到的控制量发送成功后，经过连续d次丢包，才有根据(l+d+1)T时刻状态得到的控制量在 (l+d+1+εl+d+1)T时刻作用到对象，在连续丢包期间，执行器使用最后一次接收到的控制量，故有：

将式(3)代入状态方程(1)，有

η(k)表示输入Kx(l)有效期间，当前时刻 kT与采样时刻lT之间的间隔时间。由假设(4)，η(k)是有界的，即 η(k)∈[ηm,ηM]，其中，ηm=εm,ηM=εM+dM。 式(5)可转化为：

将式(6)代入式(4)，有

综上所述，对于符合以上假设的NCSs，其数学模型式可用式(7)描述，它表示一类具有时变、有界输入时延的离散时滞系统。

2 网络控制系统的稳定性分析

以下定理给出NCSs渐近稳定的充分条件。

定理1对于给定的状态反馈增益矩阵K和标量ηm＞0，ηM＞0，如果存在适维正定矩阵 P、Q1、Q2、Z1、Z2、U、W 以及普通矩阵 F、G、H、L1、L2,使得以下矩阵不等式(8)～(11)成立，则当时变输入时延 ηm≤η(k)≤ηM时，网络控制系统(7)是渐近稳定的。

式中，

证明：定义

由状态方程(7)得到

取任意适维矩阵L1和L2，在等式(13)两边左乘2(xT(k)得到

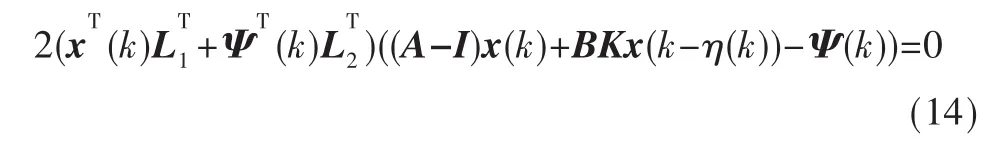
(11)约束的矩阵，对于向量 ξ(k)和 Ψ(k)，有

构造以下李雅普诺夫泛函

式中，

其中 P、Q1、Q2、Z1和 Z2均为正定矩阵。

分别对上述范函各子项计算差分，得到

由式(15)～(17)和(20)，得到

综合式(14)、(18)、(19)和(21)可得

若式(8)～(11)成立，则对于任意 ξ(k)≠0，均有

由此根据Lyapunov-Krasovskii定理，网络控制系统(7)是渐近稳定的，定理1得证。

注2：对于镇定问题，即控制器增益 K未知时，定理1的式(8)具有双线性，不易求解，可参考文献[6]的方法将定理1转化为LMI形式进行求解。

3 示例及仿真

例1：分析以下连续时间被控对象的稳定性，

假设状态反馈控制器增益K=[-3.75 -11.5]。

[3]利用自由权矩阵法计算得到的最大输入时延为0.869 5 s，即当时变输入时延小于0.869 5 s时，式(22)是稳定的。由于未考虑时延最小值大于0，并且在计算李雅普诺夫泛函差分时舍弃了某个非正交叉项，所以该结果存在保守性。

本文选择采样周期为0.01 s，将连续系统(22)离散化后转换成(7)的形式，得到离散状态方程为：

对于不同的输入时延下限ηm，利用定理 1计算得到的输入时延上限ηM如表1所示。表1结果的保守性有明显改进，例如，当时延下限ηm=0时，可行的最大输入时延ηM=103，该数值等价于连续系统的最大输入时延为1.04 s，与同类文献相比有很大提高。此外，当时延下限ηm逐渐增大时，使系统保持稳定的时延上限ηM也相应增大，由此表明，如果在稳定性判据中考虑实际时延下限大于0的因素，则可以进一步降低保守性。

表1 不同时延下限对应的可行时延上限(例1)

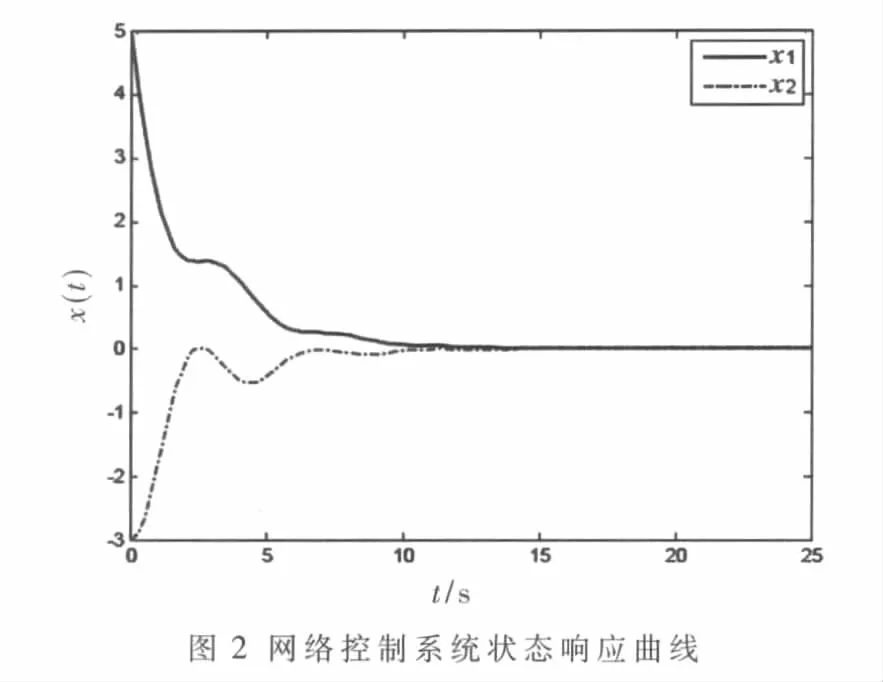
设初始状态 x(0)=[5 -3]T，采样周期为 0.01 s，传输时延为50个采样周期，连续丢包数为56个，即输入时延取表1中最大的可行时延上限106时，利用MATLIB/Simulink仿真得到的响应曲线如图2所示，由曲线可知，上述NCSs是渐近稳定的。

例2分析以下离散时间被控对象的稳定性，

参考文献[4]基于离散时滞系统理论计算得到，当输入时延上限时，系统是可镇定的，其中增益K=[0.000 5-0.130 4]。本文采用参考文献[4]的反馈增益，对于不同的时延下限ηm，利用定理1计算得到使系统保持稳定的输入时延上限ηM如表2所示，当时延下限为 0时，使系统保持稳定的最大时延上限为33，表明本文结果的保守性明显小于参考文献[4]。

本文研究了NCSs的稳定问题。将包含随机、有界时延和丢包的NCSs建模为具有时变输入时延的离散时滞模型。利用自由权矩阵法推导出基于LMI形式的渐近稳定充分条件。由于本文采用合理的上限约束技术消除了同类文献中忽略的李雅普诺夫泛函差分计算过程中产生的非正交叉项，因而保守性更小。仿真结果表明系统性能得到了明显提高。本文结论可用于分析NCSs稳定性，如果按文献[7]中方法将定理1进行适当变换，则也可用于控制器设计。

表2 不同时延下限对应的可行时延上限(例2)

参考文献

[1]李洪波,孙增圻,孙富春.网络控制系统的发展现状及展望[J].控制理论与应用,2010,27(2)：238-243.

[2]YUE D,HAN Q L,PENG C.State feedback controller design of networked control systems[J].IEEE Transactions on Circuits and Systems II：Express Briefs,2004,51(11)：640-644.

[3]XIONG J L,LAM J.Stabilization of networked control systems with a logic ZOH[J].IEEE Transactions on Automatic Control,2009,54(2)：358-363.

[4]张湘,肖建.网络控制系统的输出反馈控制[J].华中理工大学学报（自然科学版）,2008,36(10)：32-36.

[5]GAO H J,CHEN T W,LAM J.A new delay system approach to network-based control[J].Automatica,2008,44(1)：39-52.

[6]FRIDMAN E,SEURET A,RICHARD J P.Robust sampleddata stabilization of linear systems：an input delay approach[J].Automatic,2004,40(8)：1441-1446.