获取目标最佳极化算法的FPGA实现

陈歆炜，赵建中，吴 文

(南京理工大学 近程高速目标探测技术国防重点实验室，江苏 南京 210094)

在雷达系统中，当以某目标的最佳极化方式发射电磁波时，该目标回波在接收天线端的功率能够达到最大。相干情况下，目标最佳极化的Jones矢量就是其Graves功率矩阵最大特征值所对应的特征矢量[1]。通常，系统通过计算Graves功率矩阵的特征值和特征矢量来获取目标的最佳极化，使得在发射功率不变的前提下提高目标回波的信噪比。在弹载、车载、机载、星载等对体积有限制的小型化系统中，需使用数字信号处理芯片（如FPGA）求解矩阵特征值的相关问题。

Jacobi方法是计算矩阵特征值问题常用计算机算法之一。在FPGA中，基于CORDIC算法的硬件结构可简化Jacobi方法复杂的旋转操作，节约硬件资源[1-2]。然而，CORDIC算法中的多次迭代操作，使得系统处理时间成倍增加，并不适合在对实时性要求较高的系统中使用。参考文献[3]对Jacobi方法进行了并行改进，使用多个处理器并行处理的方法同时消去待求矩阵的多个非对角元素，获得了较高执行效率。但是，多个处理器的结构需要消耗大量资源，在体积和成本受到限制的小型化系统上难以实现。

为了在单处理器系统上实现实时处理，本文针对目标Graves功率矩阵的特点，提出了一种获取目标最佳极化的FPGA实现方法。文章提出了一种带门限的序列Jacobi方法，采用并行结构设计FPGA，合理调整了有限状态机（FSM）的执行时序，并对相关进程进行并发处理，压缩了程序执行时间。FPGA实现结果表明，该方法提供了快速的特征值和特征矢量求解过程，且比CORDIC算法快21%以上。

1 带门限的序列Jacobi方法

电磁波极化理论指出，目标Graves功率矩阵是复矩阵，无法直接通过Jacobi方法求解特征值。可将矩阵G表示为一个实数矩阵A和纯虚数矩阵B之和，即：

设矩阵C为：

通过求解矩阵C的特征值和特征向量，即可得到矩阵G对应的特征值及其特征向量[4]。

令C0=C，依次作迭代：

其中Rm为平面(p,q)上的一个旋转矩阵，使得矩阵Cm-1的某个非对角元素化为 0。

在传统Jacobi方法中，每次旋转前都需进行模最大非对角元素的搜索，这个过程会占用大量的时间，影响系统的实时性。本文在设计中省略了上述搜索步骤，将整个计算过程改进为“访问-旋转”两个步骤。矩阵的非对角元素可按图1所示(p,q)的取值顺序进行访问。

在实际运算过程中可设定一门限，一旦非对角元素的绝对值超过该门限，则进行Jacobi旋转；反之则维持原矩阵不变。若按图1所示顺序访问各非对角元素后并未发生一次旋转，则认为矩阵已经在预设精度下完成对角化，并输出矩阵特征值和特征矢量，从而获得目标的最佳极化。该方法的收敛性以及门限的选取已在参考文献[4]中进行了讨论。

2 FPGA硬件设计

根据第1节所述的算法，在FPGA中计算矩阵特征值和特征矢量的流程如图2所示。

图2 计算矩阵特征值和特征矢量的流程图

图3所示为本文设计的一种可实现上述流程的FPGA结构。该结构中，直接用乘法器和加法器模块替代了通常为完成旋转运算所设计的CORDIC模块。

图3所示的结构中各模块的具体功能如下：

ROM：存储在运算过程中无需实时改变的信息。

双端口RAM：储存待求矩阵和矩阵的特征矢量。

有限状态机(下文简称为状态机)：负责控制执行过程中的时序，并产生地址信号对相关ROM和RAM进行访问。

比较器：将矩阵的非对角元素与预设门限进行比较，以确定是否要进行旋转。

旋转角计算模块：计算旋转角的值，并将其翻译为地址信号，用以访问存储三角函数值的ROM。

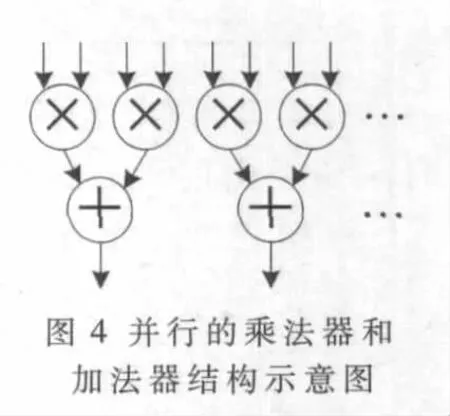
运算模块：完成一次矩阵Jacobi旋转和特征矢量的更新。该模块中的乘法器和加法器采用如图4所示的全并行结构实现，可获得较高的执行速度。

数据选择/分配器：根据不同的计算内容 （Jacobi旋转或特征矢量更新）选择输入运算模块的数据,或者将计算结果输出到相应的数据总线。

假设系统在执行了m次门限比较和n次Jacobi旋转后，得到了最终结果。经过合理设计的状态机时序示意图如图5所示。

由于门限比较的结果有可能会导致系统跳过Jacobi旋转过程，图5所示门限比较的执行次数一般多于Jacobi旋转的执行次数，即m≥n。根据上文所述求解步骤，m的极大值为6n。由于两次Jacobi旋转之间有较长时间间隔，此时运算模块处于空闲状态。本文则利用这段时间执行特征矢量的更新过程，从而提高了运算模块的使用效率。需要注意的是，特征矢量更新过程须在下一次旋转角计算进程之前开始，以免由于旋转角值的改变，导致特征矢量计算错误。

根据图5所示时序,完成整个求解过程所耗时间T可表示为：

3 FPGA实现结果与分析

根据第2节所述的结构和时序，本文在Altera公司Cyclone系列的FPGA EP1C12上实现了获取目标最佳极化的算法。数据格式采用16 bit定点格式，并将决定是否旋转的门限设为10-3。FPGA的资源消耗情况如表1所示。

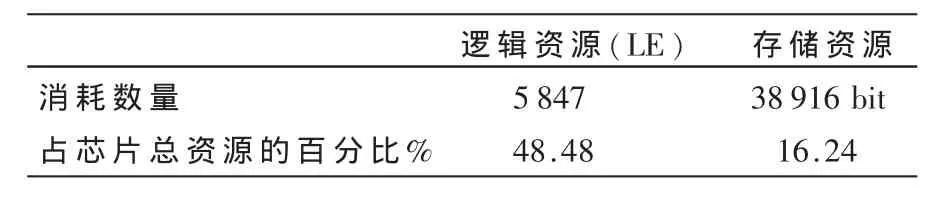
表1 FPGA的资源消耗情况

当输入随机选取的6个不同Graves矩阵时，FPGA完成整个求解过程所需要的时间如表2所示。

表2 FPGA的运算时间

由表2可知，FPGA的求解时间基本稳定，执行时间的浮动是由门限比较过程的执行次数不同引起的。

根据式(4)，可估算使用本文所提方法计算矩阵特征值和特征矢量的执行时间最多为：

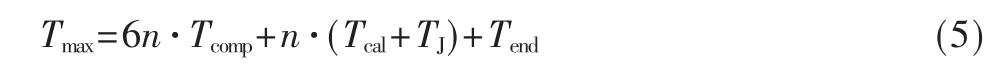
若使用参考文献[1]所提CORDIC算法实现时，因其只包含两个CORDIC模块(一个模块计算旋转角θ，另一个模块实现矩阵旋转),从而完成一次矩阵Jacobi旋转并更新特征矢量需执行两次CORDIC运算。因此，参考文献[1]的FPGA的平均执行时间T′可表示为：

其中,TC为CORDIC模块完成一次旋转所需要的时间，Tother为结构中其他模块的总耗时。

根据相关资料[5-9]，可估算出各种模块的FPGA执行时间，如表3所示。

由式(5)、式(6)和表3可得：

表3 各模块的执行时间（估算）

由式(7)可知，Tmax＜T′，表明本文所提方法的执行速度优于参考文献[1]所提的CORDIC算法，且性能可提升21%以上。

本文根据带门限的序列Jacobi算法理论,设计了一种新的FPGA硬件结构，可快速获取目标最佳极化的Jones矢量。文中对FPGA程序的执行流程、模块结构、状态机的时序作了详细讨论。FPGA实现结果表明，该方法的执行速度优于常用的CORDIC算法，可在小型化系统中实时获取目标的最佳极化。

[1]BRAVO I,MAZO M,LAZARO L J,et al.Novel HW architecture based on FPGAs oriented to solve the eigen problem[J].IEEE Transaction on Very Large Scale Integration(VLSI)Systems,2008,16(12)：1722-1725.

[2]袁生光,沈海斌.基于Jacobi算法对称矩阵特征值计算的FPGA实现[J].机电工程,2008,25(10)：80-82.

[3]王飞,王建业,张安堂,等.实对称矩阵特征值分解高速并行算法的FPGA实现[J].空军工程大学学报(自然科学版),2008,9(6)：67-70.

[4]WILKINSON J H.The algebraic eigenvalue problem[M].New York：Oxford University Press,1965：174-282.

[5]KOLOUCH J.Combinational divider in FPGA[C].Proceedings of International Conference Radioelektronika,Brno,Czech republic,Apr.24-25,2007：1-4.

[6]GURUMURTHY K S,PRAHALAD M S.Fast and power efficient 16×16 array of array multiplier using vedic multiplication[C].Proceedings of IMPACT Conference,Taipei,China,Oct.20-22,2010：1-4.

[7]DESCHAMPS J P,SUTTER G.Decimal division：Algorithms and FPGA implementations[C].Southern Programmable Logic Conference Proceedings,Ipojuca,Brazil,Mar.24-26,2010：67-72.

[8]VACHHANI L,SRIDHARAN K,MEHER P K.Efficient FPGA realization of CORDIC with application to robotic exploration[J].IEEE Transactions on Industrial Electronics,2009,56(12)：4915-4928.

[9]ARNOLD M G,COLLANGE S.A real/complex logarithmic number system ALU[J].IEEE Transactions on Computers,2011,60(2)：202-213.