RS(16,12)缩短码编译码原理及性能分析

赵 旸， 耿相铭

（上海交通大学 电子信息与电气工程学院，上海 200240）

0 引言

里德-所罗门码（RS码）是性能优良的多进制BCH码，相比于其他线性分组码，在同样的编码效率下，RS码具有较强的纠错能力，特别是在短的中等码长下，其性能很接近于理论值，不但可以纠正随机错误、突发错误及两者的结合，而且可以用来构造其他码类，如RS码和卷积码构成的级联码已经被用在深空通信的下行链路中，因此RS码在数字存储和通信系统中获得了广泛应用，例如用于CD-ROM、DVD和陆地数字传输中定义在GF(28)上的缩短RS码。

一般来说，对于定义在有限域GF(2m)符号位宽度为m的RS码，其码字长度n等于2m-1，这类RS码称为系统码或全码。在工程应用中，要使RS码具有较高的实时性，一般选用码字长度较短的码型；另外还需要灵活配置码率。对于系统码，可选的短码类型较少，因此常常通过截短系统码信息位码元符号个数的方法来得到合适的码字长度，即构造缩短码，这样不仅可以满足系统实时性的要求，还可以根据需要获得不同的码率。

1 RS编译码原理

1.1 编码原理

RS码是线性分组码，编码的过程即是根据k个信息码元及(n, k, t)RS码的特性获得n-k个校验码元的过程。

GF(2m)上的本原元为α，则生成多项式为[1]：

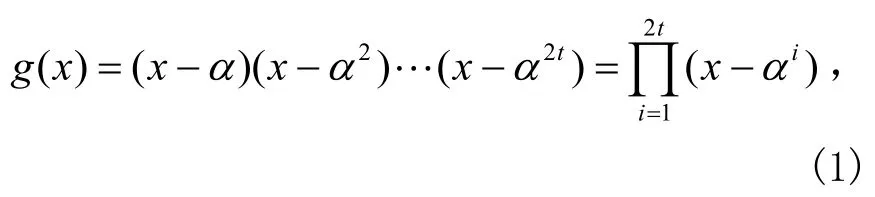
假设m=(m0, m1,…,mk-1)表示GF(2m)上的k个信息符号序列，可写成信息多项式为：

则可以按如下方法构造码字多项式C( x)：首先将信息多项式左移r=n-k位，得到m( x)·xn-k，然后用m( x)·xn-k除以生成多项式g( x)得到商式h( x)和余式r( x)：

所得到的余式r( x)就是校验多项式，其次数为r=n-k次；然后令C( x)=xn-km( x)+r( x)，即将信息位放置于码字前半部分，监督位放置于码字的后半部分，就得到编码后的码字多项式C( x)。RS码的编码电路如图1所示。

图1 RS码编码电路

1.2 译码原理

RS码译码的一般流程为[2]：

1) 由接收码字R( x)计算伴随式。

2) 根据伴随式及Berlekamp_Messey算法求出错误位置多项式σ(x)。

3) 用钱搜索法解出错误位置多项式σ(x) 的根，从而得到错误数及确定错误位置。

4) 利用 Forney算法求得错误位置上的错误值，从而得到错误图样E( x)。

5) 在RS码的纠错范围内，即错误数l不大于t时，R( x)+E( x)=C( x)，完成纠错。

译码流程如图2所示。

1.2.1 计算伴随式

根据接收信息多项式R( x)，可以得到最多纠正t个差错的RS码的伴随式：

式中,α是有限域GF(2m)的本原元。

假设发端发送的码字多项式为：

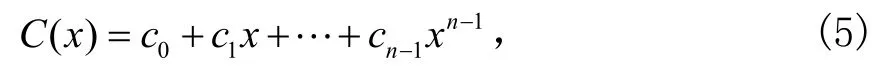
收端收到的码字多项式为：

由信道产生的错误图样多项式为：

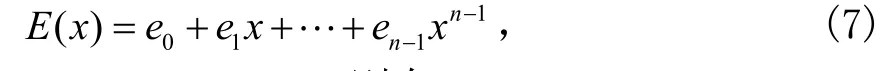
而R( x)=C( x)+E( x)，则有：

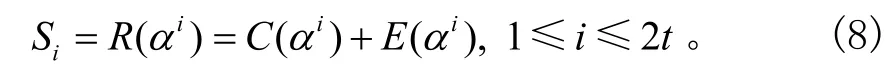
容易证明α1, α2,…,α2t均为发送码字多项C( x)的根，即C(αi)=0(1≤i≤2t )，因此：

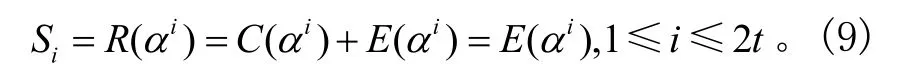
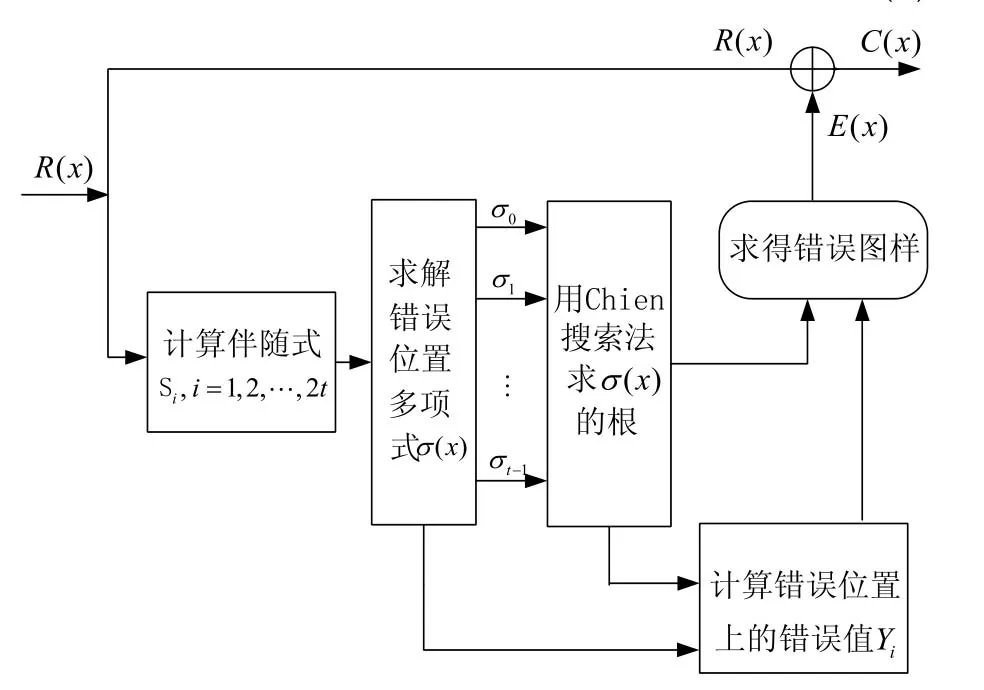
图2 RS码编码电路

可知伴随式Si只与误差多项式E( x)有关，如果所有的2t个伴随式都为0，说明(e0, e1,…,en)=0，即错误个数为 0；否则说明编码信号在信道传输过程中产生了误码。

根据伴随式的计算公式：

可以采用高效的迭代算法——Horner准则来计算伴随式的值[3]：

伴随式计算示意如图3所示。

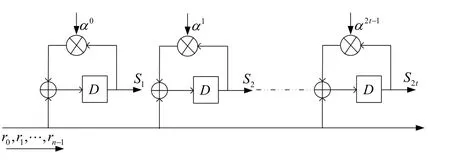
图3 伴随式计算示意

1.2.2 译码核心模块

定义错误位置多项式为：

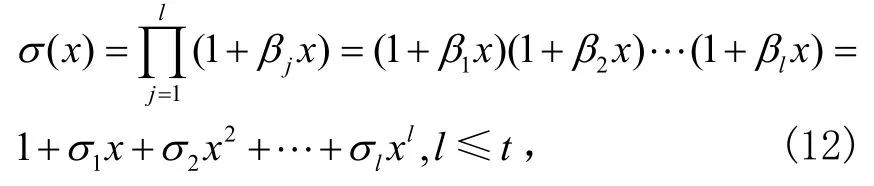
式中，l表示错误符号数，l≤t时可以正确纠正这l个误码，显然是式(12)的根，定义错误值多项式为：

另外，定义伴随式多项式S( x)为：

则这三者满足方程:

式(15)称为关键方程，关键方程的求解是RS译码算法的核心部分。工程应用中往往利用BM迭代算法结合钱搜索法求解错误位置，Forney算法求解错误值。

BM算法就是利用一个迭代过程求解关键方程，即以σ(0)(x)=1,ω(0)(x )=1为初始条件，然后通过迭代计算得到σ(k)(x)和ω(k)(x)以满足：

当k=2t时得到满足关键方程的错误位置多项式σ(2t)(x)和错误值多项式ω(2t)(x)。具体迭代过程如下[4]：

初始条件：

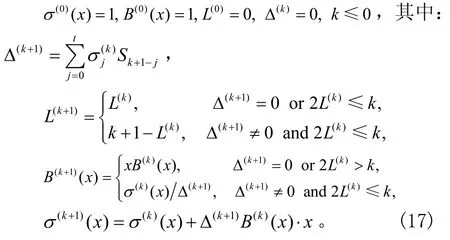
多项式σ(2t)(x)就是错误位置多项式σ(x)。

在求得错误位置多项式后，下一步是如何求出错误位置多项式的根以确定错误位置，钱闻天教授提出了著名的Chien搜索算法，该方法为一种穷举搜索法，即对码的每个位置逐位予以检索来确定错误位置。

由式(12)可知错误位置多项式：

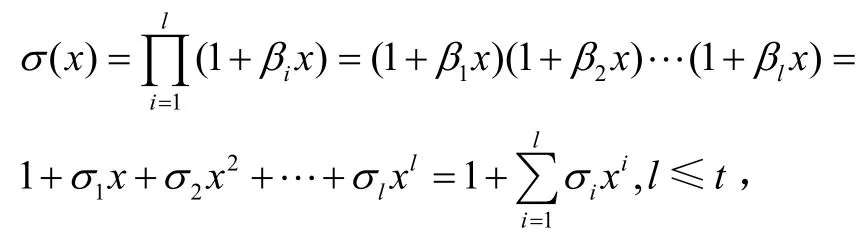
那么Chien搜索算法即是要验证：

对于接收序列，依据上式对每一个α-j(j=0,1,…,n -1)检验，即可检出第j个接收符号是否出错，该过程就是Chien搜索。

在得到错误位置后，由于RS码是非二进制码，所以还要求第j个错误位置上对应的错误值，这一步利用Forney公式计算：

求得错误位置和错误值后，将错误值与错误位置上的接收符号模2相加，即可纠正误码。

1.3 RS(16,12)缩短码的编译码

每个缩短码RS( n, k)，都有一个系统码RS( n1, k1)作为其母码，这里 n1=2m-1，m表示构成每个RS符号所需的比特数，而且 k1-k=n1-n 。对于RS(16,12)缩短码，m可以选择 5，6，7，8…，只需要满足2m＞16。为了计算方便，选择m=8，即一个RS符号占1 byte（8 bit）。那么RS(16,12)缩短码的母码为系统码RS(255,251)。

由于缩短码和其母码校验位数相等，即2t=n1-k1=n-k ，因此它们具有相同的纠错能力。缩短码的常用构造方法是将一帧系统码信息位的前k1-k个符号置零，即符号 c250=c249=…=c12=0。但是在缩短码的编译码过程中，并不需要对前k1-k个符号为0的系统码进行编译码，然后去除冗余的长0串，这是因为删去长零码元并不会对Horner编码、伴随式计算、BM迭代过程等运算模块产生影响。利用系统码的编译码电路，可以实现缩短码的编译码。

根据式(18),在RS码译码中的Chien搜索模块中，需要验证[5]：

对于接收序列，依据该式对每一个α-j(j=0,1,…,n -1)检验，即可检出第 j个接收符号是否出错。RS系统码要从第n1-1个接收符号处开始搜索，即从α-(n1-1)开始代入式(18)检验。而缩短RS码的高n1-n个信息位符号数据被截去了，没有经过信道传输也就不可能发生错误，所以α-(n1-1)，α-(n1-2)，…,α-n不可能是的根，在Chien搜索中不需要对它们进行计算，只需要对指数表中的后n个值，即α-(n-1)，α-(n-2)，…，α-0进行搜索。利用该方法可以省去n1-n步 Chien搜索，当n1-n值较大时，可以大大降低译码延时。对于RS(16,12)缩短码，每一帧可以省去239步Chien搜索，性能大幅优化。

2 性能仿真

按照图4的步骤对RS(16,12)缩短码纠错性能进行仿真分析。

RS(16,12)缩短码采用QPSK调制，使用高斯白噪声信道和瑞利衰落信道两种信道模型分别MATALAB仿真，计算采用RS编码和不采用RS编码的信号经过信道传输后的误符号率（SER）。之所以计算 SER而非误比特率（BER），是为了突出体现RS编码在纠正突发性错误方面的优势：对于一个GF(28)上的RS码符号由 8比特构成，因此在一个RS符号内纠正1比特随机错误和纠正8比特突发连续错误没有区别。RS码符号在传输中产生错误的过程如图5所示。

1 024 帧数据mi=(mi0,mi1,…,mi11)经过RS编码、调制后送入信道，i=0,1,…,1023，在收端解调、RS译码后计算出SER_RS；与原始1 024帧数据不经过RS编码直接调制后在信道中传输，收端计算出的SER_NORS进行比较。信道模型分别为高斯白噪声信道和瑞利衰落信道（多普勒频移10 Hz），如图6和图7所示。

通过软件仿真可以看出，RSN=9.5 dB时，对于高斯白噪声信道和瑞利衰落信道（多普勒频移10 Hz），通过RS(16,12)编码可以将误符号率分别提高2个和1个数量级。说明RS编码具有优良的纠错性能，尤其适合于纠正信道传输过程中产生的突发连续错误。

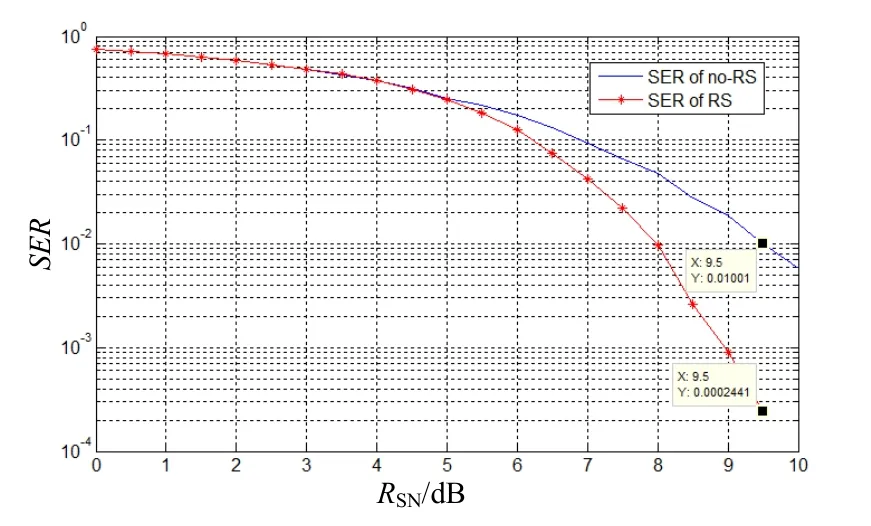
图6 高斯白噪声信道下SER

图7 瑞利衰落信道下SER

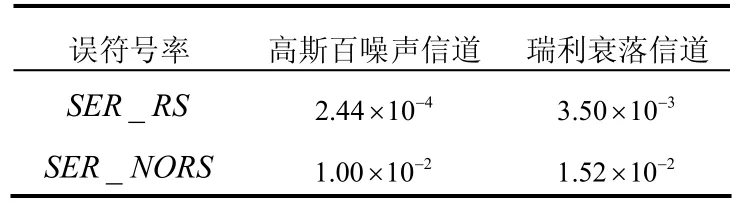
表1 9.5 dB下信道传输SER比较

3 结语

文中在分析RS系统码编译码原理的基础上给出了RS(16,12)缩短码的切实可行的编译码方案，由此可以看出RS码低复杂度的优点。并对RS(16,12)码在高斯白噪声信道和瑞利衰落信道下的纠错性能进行软件仿真和分析，可以看出RS码在低信噪比条件下、误码数超过其纠错能力时纠错性能并不明显，但随着信噪比的提高，可以大幅提高误符号率和误比特率，而RS码本身的特性使其具有很强的突发连续错误检错能力。这些优点使得RS码在工程中得到了广泛应用。

[1] 宋洋军，权进国，林孝廉.DMR标准RS码编译码器的FPGA实现[J].通信技术，2010，43(06):13-15.

[2] 王海东.Reed-Solomon码在 MPEG-4视频流传输中的应用[J].通信技术，2007，40(05):56-64.

[3] SWEENEY P. 差错控制编码[M].俞越，张丹译.北京：清华大学出版社，2004：122-138.

[4] MORELOS-ZARAGOZA R. 纠错编码的艺术[M].张力军译.北京：北京交通大学出版社，2007:79-91.

[5] 王景煜，景晓军.基于BM算法的RS(18,10)的译码的软件实现和性能分析[J].通信技术，2010，43(04):70-71.